
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Вычисление циркуляции дифференцируемого векторного поля по границе ориентированной поверхности
|
|
Рассмотрим теперь произвольное векторное поле  , определенное и дифференцируемое на некоторой ориентированной поверхности
, определенное и дифференцируемое на некоторой ориентированной поверхности  , границей которой служит кусочно-гладкий путь
, границей которой служит кусочно-гладкий путь  , направление обхода которого согласовано с ориентацией поверхности
, направление обхода которого согласовано с ориентацией поверхности  . Поставим задачу вычислить циркуляцию
. Поставим задачу вычислить циркуляцию 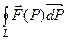 .
.
Разобьем поверхность  на достаточно большое число малых частей. Пусть это будет разбиение
на достаточно большое число малых частей. Пусть это будет разбиение  . Обозначим через
. Обозначим через  границу поверхности
границу поверхности 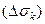 , направление обхода которой согласовано с ориентацией этой поверхности, унаследованной от поверхности
, направление обхода которой согласовано с ориентацией этой поверхности, унаследованной от поверхности  , а через
, а через  - площадь поверхности
- площадь поверхности 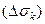 . Пусть
. Пусть  - наибольший из диаметров частичных поверхностей. Величина
- наибольший из диаметров частичных поверхностей. Величина 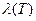 называется рангом разбиения поверхности
называется рангом разбиения поверхности  и служит показателем того, насколько мелким это разбиение является. Выберем на каждой из частичных поверхностей точку
и служит показателем того, насколько мелким это разбиение является. Выберем на каждой из частичных поверхностей точку  ,
,  . Согласно свойству аддитивности циркуляции векторного поля, (см. (4.3)) справедливо равенство
. Согласно свойству аддитивности циркуляции векторного поля, (см. (4.3)) справедливо равенство
 . (4.19)
. (4.19)
Следовательно, вычисление циркуляции по границе всей поверхности сводится к вычислению циркуляций по границам ее частей, которые можно считать сколь угодно малыми по своим размерам. Рассмотрим какой-нибудь из интегралов  ,
,  и представим переменную интегрирования в виде
и представим переменную интегрирования в виде  . Поскольку точка
. Поскольку точка  находится на границе поверхности
находится на границе поверхности 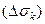 , а
, а  , можно считать, что вектор
, можно считать, что вектор  имеет сколь угодно малую длину. По условию, векторное поле
имеет сколь угодно малую длину. По условию, векторное поле 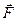 дифференцируемо во всех точках поверхности
дифференцируемо во всех точках поверхности  , в том числе в точке
, в том числе в точке  , так что справедливо приближенное равенство
, так что справедливо приближенное равенство
 . (4.20)
. (4.20)
Выберем в пространстве некоторое начало отсчета  и положим
и положим  ,
,  ; тогда
; тогда  . Поскольку производная векторного поля
. Поскольку производная векторного поля  есть линейный оператор, справедливо равенство
есть линейный оператор, справедливо равенство  . Следовательно, равенство (4.20) можно переписать так
. Следовательно, равенство (4.20) можно переписать так
 , (4.21)
, (4.21)
где  - постоянный вектор. Пусть
- постоянный вектор. Пусть  - какая-нибудь декартова система координат, а
- какая-нибудь декартова система координат, а  - разложение вектора
- разложение вектора  . Тогда, очевидно, справедливо равенство
. Тогда, очевидно, справедливо равенство  , где
, где  - скалярное поле, представленное функцией
- скалярное поле, представленное функцией  в рассматриваемой декартовой системе координат. Таким образом, постоянное векторное поле потенциально, так что циркуляция такого поля по любому замкнутому пути равна нулю. С учетом сказанного приходим к равенству
в рассматриваемой декартовой системе координат. Таким образом, постоянное векторное поле потенциально, так что циркуляция такого поля по любому замкнутому пути равна нулю. С учетом сказанного приходим к равенству
 , (4.22)
, (4.22)
причем относительная погрешность приближенного равенства будет сколь угодно малой при достаточно малых размерах поверхности 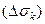 .
.
Рассмотрим интеграл в правой части равенства (4.22). Для заданного начала отсчета  , при выполнении условия
, при выполнении условия  , он представляет собой циркуляцию линейного векторного поля
, он представляет собой циркуляцию линейного векторного поля  по границе ориентированной поверхности
по границе ориентированной поверхности 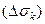 . Поскольку поверхность
. Поскольку поверхность 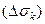 ориентирована, в каждой ее точке
ориентирована, в каждой ее точке  определен вектор нормали
определен вектор нормали  , который меняется непрерывно при переходе из одной точки в другую. Поэтому при достаточно малых размерах поверхности
, который меняется непрерывно при переходе из одной точки в другую. Поэтому при достаточно малых размерах поверхности 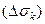 справедливо приближенное равенство
справедливо приближенное равенство  ,
,  , погрешность которого может считаться сколь угодно малой. Другими словами, при достаточно малых размерах поверхность
, погрешность которого может считаться сколь угодно малой. Другими словами, при достаточно малых размерах поверхность 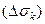 может рассматриваться как плоская и, следовательно, согласно формуле (4.18), справедливо приближенное равенство
может рассматриваться как плоская и, следовательно, согласно формуле (4.18), справедливо приближенное равенство
 ,
,
где  . Учитывая (4.20), приходим к приближенному равенству
. Учитывая (4.20), приходим к приближенному равенству
 ,
,
погрешность которого будет сколь угодно малой при достаточно малых размерах поверхности 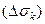 . Полагая, как и выше,
. Полагая, как и выше,  , получаем
, получаем
 . (4.23)
. (4.23)
С учетом формулы (4.23) равенство (4.19) представляется в виде
 .
.
Продолжая процесс дробления поверхности  на все более мелкие части и следя за тем, чтобы ранг разбиения стремился к нулю, в пределе получаем точное равенство
на все более мелкие части и следя за тем, чтобы ранг разбиения стремился к нулю, в пределе получаем точное равенство
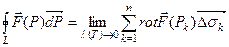 . (4.24)
. (4.24)
Как мы знаем, ротор векторного поля по определению есть ротор матрицы его производной. Если матрица производной в рассматриваемом базисе  имеет компоненты
имеет компоненты  ,
,  , то, как уже говорилось, ее ротор вычисляется по формуле
, то, как уже говорилось, ее ротор вычисляется по формуле
 .
.
Пусть  - некоторая декартова система координат в пространстве
- некоторая декартова система координат в пространстве  , а
, а  - координаты векторного поля
- координаты векторного поля  в базисе
в базисе  . Тогда, согласно (2.13), матрица производной векторного поля
. Тогда, согласно (2.13), матрица производной векторного поля  в рассматриваемом базисе выражается формулой
в рассматриваемом базисе выражается формулой
 .
.
Отсюда следует, что ротор векторного поля в декартовых координатах выражается формулой

|
Просмотров 560 |
|
|
