Вычисление определенного интеграла методом Монте-Карло

Вычисление кратных интегралов.

Рассмотрим на примере двойного интеграла

.

Одним из способов вычисления этого интеграла является метод ячеек. Рассмотрим случай, когда областью интегрирования является прямоугольник: .

По теореме о среднем найдем среднее значение функции :

, . (*)

Будем считать, что среднее значение приближенно равно значению функции в центре прямоугольника, т.е. .

Тогда из (*) получим выражение для приближенного вычисления двойного интеграла:

,

, .

Точность этой формулы можно повысить, если разбить область на прямоугольные ячейки :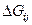

, .

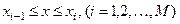Для каждой из ячеек получаем

.

Значение двойного интеграла определяется как сумма выражений по всем ячейкам:

.

В правой части стоит интегральная сумма и при неограниченном уменьшении периметров ячеек (или стягивании их в точки) эта сумма стремится к значению интеграла для любой непрерывной функции .

Если область интегрирования непрямоугольная, то в ряде случаев ее целесообразно привести к прямоугольному виду путем замены соответствующих переменных.

Например пусть область задана в виде криволинейного четырехугольника: . Данную область можно привести к прямоугольному виду с помощью замены

, .

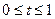Другим довольно распространенным методом вычисления кратных интегралов является их сведение к последовательному вычислению определенных интегралов. Для прямоугольной области можно записать в виде

, .

Если область интегрирования имеет более сложную форму, то она либо приводится к прямоугольному виду с помощью замены переменных, либо разбивается на простые элементы.

Для вычисления кратных интегралов используется также метод замены подынтегральной функции многомерным интерполяционным многочленом. Вычисление коэффициентов этих многочленов для простых областей не вызывает затруднений.

Существует ряд других численных методов вычисления кратных интегралов. Среди них особое место занимает метод статистических испытаний (метод Монте-Карло).

Вычисление определенного интеграла методом Монте-Карло.

Во многих задачах исходные данные содержат случайный характер, поэтому для их решения должен применяться статистико-вероятностный подход. На таком подходе пострен метод статистических испытаний (метод Монте-Карло).

Метод Монте-Карло состоит в том, что рассматривается некоторая случайная величина , математическое ожидание которой равно искомой величине :

.

Проводится серия независимых испытаний, в результате которых генерируется последовательность случайных чисел , и по совокупности этих значений приближенно определяется искомая величина

,

.

Пусть ‑ равномерно распределенная на отрезке [0, 1] случайная величина, т.е. ее плотность распределения задается условием

Тогда любая функция также будет случайной величиной, и ее математическое ожидание равно

.

Следовательно, читая это неравенство в обратном порядке, приходим к выводу, что интеграл может быть вычислен как математическое ожидание некоторой случайной величины , которая определяется независимыми реализациями случайной величины с равномерным законом распределения:

.

Аналогично можно определить и кратные интегралы. Для двойного интеграла получим

,

где поверхность : , а ‑ независимые реализации случайных величин , равномерно распределенных на отрезке [0, 1].

Раздел. Численное решение

обыкновенных дифференциальных уравнений

Общие сведения.

Методы решения задачи Коши.

3. Одношаговые методы: Эйлера и его модификации, Рунге-Кутта.

4. Многошаговые методы: прогноза-коррекции Адамса, Милна.