Виведення рівняння поширення тепла. Постановка крайових задач і задачі Коші

Розглянемо поширення тепла в однорідному стрижні довжини l (Рис. 1).

0 х₁ х₂ l х

Рис. 1

Будемо припускати, що бічна поверхня стрижня є непроникною для тепла, тобто є теплоізольованою, а стрижень настільки тонкий, що у кожен момент часу в усіх точках поперечного перерізу стрижня його температура однакова. Розташуємо вісь Ох так, що один кінець стрижня буде збігатися з точкою , а другий – з . Нехай - температура в перерізі стрижня з абсисою х в момент часу t . Припускається, що початкова температура стрижня є відомою функцією від х, а кінці стрижня підтримуються при температурі , .

Процес поширення тепла у стрижні таким чином відбувається завдяки можливому неоднорідному розподілу температури на початку процесу, а також із-за нерівності температур на торцевих перерізах стрижня.

Поставимо завдання вивести диференціальне рівняння такого процесу. Його виведення базується на ряді фізичних уявлень. Дослідним шляхом встановлено, що кількість тепла, яке протікає через поперечний переріз стрижня s з абсцисою х за час (тепловий потік), визначається формулою

, (39)

де k – коефіцієнт теплопровідності матеріалу стрижня. Припустимо, що коефіцієнт теплопровідності сталий. Це припущення виправдовується, якщо стрижень однорідний, а температура змінюється у невеликих межах.

Дослідним шляхом встановлено також, що кількість тепла, яке необхідно надати однорідному тілу об’єму v, щоб підвищити його температуру на величину , дорівнює

, (40)

де густина тіла, с – його питома теплоємність.

Розглянемо елемент стрижня, обмежений перерізами з абсисами і (Рис. 1), де і - довільні фіксовані значення , і складемо для нього рівняння теплового балансу. Згідно з формулою (39) кількість тепла, що проходить через переріз з абсисою за час , дорівнює

;

те ж саме для перерізу з абсисою

.

Надходження тепла в елемент стрижня за рахунок проходження через нього теплового потоку за час буде дорівнювати

.

Для перетворення різниці в дужках застосовуємо Лагранжову теорему: якщо функція неперервна на замкненому проміжку і має похідну у кожній внутрішній точці цього проміжку, то знайдеться принаймні одна така точка , що для неї справджується рівність

.

Вираз для при цьому стає

. (41)

Надходжене тепло за час згідно з законом збереження витрачається на підвищення температури елемента стрижня на величину, яку позначимо .

Згідно з (40) кількість тепла, яке потрібно витратити на підвищення температури елемента стрижня, що розглядається, на величину за час , дорівнює ; тут .Для достатньо малих проміжків часу і ,

Тому

. (42)

Наближена рівність (42) буде тим точнішою, чим меншим буде .

Згідно з законом збереження тепла

.

Ця рівність з урахуванням (41), (42) стає

. (43)

Щоб ця рівність перетворилася на точну, потрібно, скоротивши на , зробити граничний перехід . Далі поділимо (43) на і спрямуємо , при цьому і оскільки 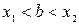, то . Але довільне значення . Тобто, при значення можна замінити на довільне значення . Нарешті, поділимо (43) на і дістанемо остаточне рівняння

, (44)

де коефіцієнт температуропровідності.

При математичному моделюванні поширення тепла рівняння (44) доповнюється межовими (або крайовими) умовами, а також початковими умовами. Їх наявність дозволяє моделювати певний процес поширення тепла, який ці додаткові умови характеризують. Математичний зміст межових умов у даній задачі випливає з їх фізичного змісту. Оскільки початок стрижня збігається з початком координат , а його кінець має абсцису , то межові умови для температури згідно з умовами на торцевих перерізах стрижня набирають вигляд

. (45)

За умовою задачі початкова температура стрижня , є відомою функцією від х, позначимо її . Тоді початкова умова для задачі, що розглядається, набирає вигляду

. (46)

Виведення рівняння теплопровідності (44) і формулювання математичного змісту межових умов (45) та початкової умови (46) дозволяють сформулювати математичний зміст фізичної задачі поширення тепла, поставленої на початку цього розділу. Отже, поставлена фізична задача зводиться до знаходження розв’язку рівняння (44) на відрізку при , який задовольняє межові умови (45) при і початкову умову (46) при . Задача (44) − (46) називається межовою (або крайовою) задачею для рівняння (44).

Для рівняння теплопровідності (44) крім межової задачі можна поставити задачу Коші:

знайти розв’язок рівняння теплопровідності (44) при і , який задовольняє початкову умову

при . (47)

Задача Коші (44), (47) виникає при вивченні поширення тепла у дуже довгому стрижні з теплоізольованою бічною поверхнею, коли межовими умовами (45) можна знехтувати. Такий стрижень при розв’язанні задачі вважається нескінченним. Поширення тепла у такому стрижні визначається тільки його початковою температурою (47).

Тригонометричні ряди Фур’є