Тригонометричним рядом Фур’є функції на інтервалі за загальною тригонометричною системою функцій

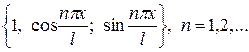(48)

називається функціональний ряд виду

, (49)

коефіцієнти якого визначаються за формулами

, (50)

(51)

(52)

Приклад 1. Розвинути за загальною тригонометричною системою функцій (48) на відрізку функцію

Функція задається різними аналітичними виразами на різних ділянках інтервалу . Тому для обчислення інтегралів, які містять цю функцію, представимо їх у вигляді суми двох інтегралів: від – 1 до 0 і від 0 до 1;

Обчислимо одержані інтеграли.

.

Звідси отримуємо, що

Обчислимо :

Обчислимо :

Обчислимо одержані інтеграли.

Це дозволяє обчислити остаточно :

.

Отже, розвинення даної функції в ряд Фур’є за загальною тригонометричною системою функцій (1) набирає вигляду

Відомо, що якщо функція парна, тоді при її інтегруванні за симетричними межами справедлива формула

(53)

Якщо функція непарна, тоді інтеграл від неї за симетричними межами дорівнює нулю

. (54)

Такі властивості визначених інтегралів від парних та непарних функцій дозволяють отримати частинні випадки тригонометричного ряду (49).

Якщо функція парна, то підінтегральна функція у (52) 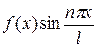буде непарною. Тоді у розвиненні (49) , а

(55)

Якщо функція − непарна, то підінтегральна функція у (51) буде непарною. Тоді у розвиненні (49) , а

. (56)

Приклад 2. Розвинути в ряд Фур’є за загальною тригонометричною системою (1) на інтервалі 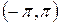функцію .

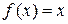Ця функція є непарною; тому всі і дорівнює нулю; стосовно , то для їх обчислення можна скористатися формулою (56)

Отже,

Крім тригонометричного ряду Фур’є (2) за повною тригонометричною системою функцій (48) має місце ряд Фур’є за системою функцій

(57)

для функції , яка визначена на несиметричному інтервалі . Такий ряд називається рядом Фур’є за синусами

. (58)

Його коефіцієнти визначаються за формулами

. (59)

Приклад 3.Розвинути в ряд Фур’є за синусами на інтервалі функцію .

Обчислимо коефіцієнти цього ряду:

. (60)

Обчислимо окремо інтервали в дужках. Перший інтеграл обчислюється за формулою інтегрування частинами

Другий інтеграл у дужках формули (60) обчислюється так

.

Підстановка одержаних результатів у формулу (60) дає

(61)

Використання (61) в (58) для дає таке розвинення

(62)

Функція , яка визначена на інтервалі , може бути розвиненою також за системою

(63)

Такий ряд Фур’є називається рядом Фур’є за косинусами

. (64)

Його коефіцієнти визначаються за формулами

. (65)

Приклад 4. Розвинути в ряд Фур’є за косинусами на інтервалі функцію .

Обчислимо коефіцієнти цього ряду

. (66)

Обчислимо окремо інтеграли в дужках. Перший інтеграл обчислюється за формулою інтегрування частинами

Другий інтеграл у дужках формули (66) обчислюється так

.

Підстановка одержаних результатів у формулу (66) дає

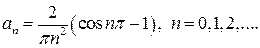
Таким чином, функція розкладається у ряд Фур’є за косинусами на інтервалі таким чином

. (67)

Ряди (62) і (66) різні, але на інтервалі вони збігаються до однієї функції.

2.3. Розв’язання задачі про поширення тепла методом Фур’є (методом відокремлення змінних)

Розв’яжемо таку задачу: знайти розподіл температури у досить тонкому стрижні з теплоізольованою бічною поверхнею, розташованому на відрізку осі Ох, якщо його кінці підтримуються при нульовій температурі, а початковий розподіл його температури при визначається відомою функцією . Математичне моделювання поширення тепла у такому стрижні у попередньому підрозділі показує, що для знаходження температури у будь-якому перерізі стрижня з координатою х ( ) у будь-який момент часу за вказаних умов слід знайти розв’язок диференціального рівняння

при , , (68)

який задовольняє межові умови

при (69)

і початкову умову

при . (70)

У задачі (68) − (70) як рівняння (68), так і межові умови (69) однорідні. Легко перевірити, що якщо деякі функції задовольняють рівняння (68) і умови (69), то будь-яка їх лінійна комбінація

де − довільні сталі, також задовольняє це рівняння і ці межові умови. Це означає, що функція

є розв’язком рівняння (68), яка задовольняє умови (69).

На вказаній властивості розв’язків рівняння (68) і базується метод Фур’є розв’язання задачі (68), (69), (70). Суть цього методу полягає у тому що на першому етапі розв’язаннязадачі (68) − (70) знаходяться частинні розв’язки рівняння (68), які задовольняють межові умови (69); нехай це будуть функції

. (71)

На другому етапі розв’язаннязадачі (68) − (70) з функцій (71) складається ряд

(72)

з довільними коефіцієнтами С_і.

Оскільки рівняння (68) і умови (69) однорідні, то функція яка визначається рядом (72) також буде розв’язком рівняння (68), який задовольняє умови (69), при любих значеннях коефіцієнтів ряду. (Зауваження.Оскільки ряд (72) нескінченний, то потрібно, щоб він збігався. Припускається також, що його також можна два рази почленно диференціювати). Для знаходження розв’язку цієї задачі (68), (69), (70) залишається підібрати довільні коефіцієнти С_і так, щоб функція (72) задовольняла також початкову умову (70).

Для здійснення цього плану розв’язання на його першому етапі шукатимемо частинні розв’язки рівняння (68), які задовольняють межові умови (69), у вигляді добутку двох функцій

(73)

кожна з яких залежить тільки від однієї змінної.

Диференціюючи два рази вираз (73) по х і один раз по t отримаємо

(Для скорочення запису ми не пишемо аргументів функцій і )

Підставимо вирази для похідних у рівняння (68), воно при цьому перетвориться на тотожність

, (74)

оскільки за припущенням вираз (73) визначає частинні розв’язки рівняння (68). Поділимо обидві частини тотожності (74) на добуток Після скорочень матимемо

(75)

Ліва частина цієї тотожності не залежить від змінної х. Оскільки (75) − це тотожність, то й її права частина не повинна залежати від х. Це означає, що вона стала, оскільки, як видно з (75), вона могла залежати тільки від х. Помічаючи, що права частина (75) не залежить від змінної t ми аналогічно переконуємося, що й ліва частина (75) не залежить від t, а, отже, є сталою.

Позначимо тепер сталу, якій повинні бути рівними ліва і права частини тотожності (75) через с. Тоді (75)розпадається на два звичайних диференціальних рівняння

які після елементарних перетворень набувають вигляду

(76)

(77)

Таким чином, застосування методу відокремлення змінних зводить розв’язання диференціального рівняння у частинних похідних (68) до розв’язання двох звичайних диференціальних рівнянь (76) і (77) зі сталими коефіцієнтами.

Оскільки ми шукаємо частинні розв’язки рівняння (68), які задовольняють крайові умови (69), то при будь-якому значенні t повинні виконуватися рівності

Якби нулю дорівнював другий множник , то розв’язок дорівнював би нулю при всіх значеннях х і t . Тому, щоб відшукати розв’язки не тотожні нулю (а тільки такі нас цікавлять), ми повинні припускати, що

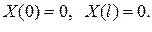(78)

В результаті для знаходження функції ми прийшли до крайової задачі: знайти розв’язки лінійного диференціального рівняння другого порядку з сталими коефіцієнтами (77), які задовольняють межові умови (78).

Почнемо з відшукання розв’язку рівняння (76). Замінимо на

і відокремимо у рівнянні змінні, домножуючи його ліву і праву частини на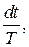

Почленне інтегрування дозволяє отримати

(79)

де довільна стала інтегрування. Поклавши і потенціюючи рівність (12), матимемо

,

або

,

де нова довільна стала. Оскільки ні в одному перерізі стрижня температура не може необмежено зростати за абсолютною величиною при , то стала с повинна бути від’ємною. Покладемо , тоді

. (80)

Рівняння (77) при цьому набере вигляду

. (81)

Для розв’язання цього лінійного диференціального рівняння другого порядку зі сталими коефіцієнтами складаємо його характеристичне рівняння

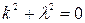. (82)

Корені характеристичного рівняння (82) – комплексно спряжені

,

тому загальний розв’язок рівняння (81) буде

. (83)

В одержаному розв’язку (83) є три невідомі сталі і . Зменшити їх кількість можна за допомогою межових умов (78), які повинен задовольняти розв’язок (83). Покладаючи у (83) , згідно з першою умовою (78) отримаємо

,

звідки . Друга умова (78) дозволяє отримати

. (84)

Припущення 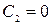, яке випливає із (84), разом з одержаним значенням приводить згідно з (83) до нульового розв’язку рівняння (81) і, як наслідок, до нульового розв’язку рівняння (68). Оскільки нас цікавлять ненульові розв’язки рівняння (68) і (81), то , і рівність (84) можлива лише при

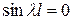, (85)

тобто при

(k не дорівнює нулю, оскільки є від’ємною величиною).

Отже, якщо 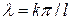, тобто, якщо , то існують розв’язки рівняння (81), а, отже, й рівняння (77), які не дорівнюють тотожно нулю. Ці розв’язки отримуються з (83) при , . При цьому розв’язок, який відповідає деякому фіксованому k, позначимо через . Він матиме вигляд

, (86)

де довільна стала. Ми маємо право надалі надавати k тільки додатні значення k=1, 2,…, оскільки за від’ємних k будуть отримуватися розв’язки того ж виду (оскільки довільні сталі, які можуть мати будь-які знаки ).

Врахуємо у (80) знайдені значення (k=1, 2,…). При цьому кожному знайденому значенню (k=1, 2,…). згідно з (80) буде відповідати розв’язок

(87)

рівняння (76), де довільні сталі.

Підставимо вирази (86) і (87) у формулу (73) і знайдемо при цьому частинні розв’язки рівняння (68), які задовольняють межові умови (69). При цьому кожному значенню k=1, 2,… буде відповідати розв’язок

, (88)

в якому позначає добуток довільних сталих .

Перейдемо тепер до другої частини методу Фур’є – побудуємо розв’язок, який задовольняє початкову умову (70). Для цього візьмемо суму розв’язків (88), яка завдяки лінійності і однорідності рівняння (1) також буде його розв’язком:

. (89)

Оскільки ми склали нескінченний ряд, то, вочевидь, необхідно, щоб він був збіжний. Припустимо також, що його можна почленно диференціювати – два рази по х і один раз по t. Ясно, що функція задовольняє крайові умови (69), оскільки їх задовольняє кожна з функцій .

Підберемо тепер довільні сталі так, щоб функція (89)задовольняла початкову умову (70). Підставимо значення в (89), враховуючи, що згідно з (70),

. (90)

Формула (90) показує, що величина є коефіцієнтами розвинення функції в ряд Фур’є по синусах в інтервалі , тобто

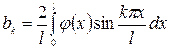. (91)

Підставлення виразів (91) для коефіцієнтів у ряд (89) визначає остаточно розв’язок задачі (68) – (70).