Умовні ймовірності. Незалежність подій

Умовні ймовірності. Теорема множення. Розглядаючи ймовірності випадкових подій, ми не мали ніякої інформації про ймовірнісний зв’язок між різними випадковими подіями. Очевидно, він існує. Якщо при обчисленні ймовірності події A не накладається додаткових умов, крім тих, якими визначається випадковий експеримент, то ймовірність називають безумовною. Але в ряді випадків необхідно обчислити ймовірності подій при додатковій умові, що настала деяка подій B, яка має додатню ймовірність. Ймовірність події A, обчислена за припущенням, що подія B уже настала, називається умовною ймовірністю події A при умові B і позначається або .

Розглянемо приклад знаходження умовної ймовірності в класичній моделі. Позначимо , , кількість елементарних подій, що спричиняють відповідно поді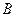ї , , . Тоді

.

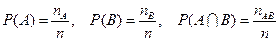Якщо подія B уже настала, то змінюються умови експерименту і у новому (умовному) експерименті число можливих наслідків буде рівне – числу елементарних подій, що спричиняють подію 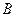, а подію A будуть спричиняти тільки ті елементарні події, які спричиняють . Тому

.

У загальному випадку умовна ймовірність вводиться за допомогою наступного означення.

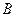Означення. Умовною ймовірністю події при умові, що подія настала з , називається число

.

Аналогічно, при виконанні умови ,

.

Введена таким чином умовна ймовірність має всі властивості ймовірності. Для перевірки цього досить показати, що виконуються аксіоми ймовірності. Із означення і властивостей ймовірності випливає:

1) ,

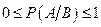2) ,

3) ,

4) якщо , то ,

5) якщо – послідовність попарно несумісних подій ( при ), то .

6) .

Із означення умовної ймовірності одержуємо твердження, яке називається теоремою множення ймовірностей.

Теорема 1. Якщо і , то

.

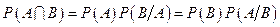Теорема 2. Якщо – такі випадкові події, що , тоді

( загальна теорема множення ймовірностей).

Приклад 1. В урні є 10 куль: 3 білих і 7 чорних. Із урни випадково вибирають дві кулі. Знайти ймовірність того, що вибрані кулі будуть білі.

Розв’язування. Експеримент, що розглядається в даній задачі, полягає у виборі двох куль із десяти. Нехай A – подія, яка полягає у тому, що перша вибрана куля буде білою, а B – друга вибрана куля буде білою. Тоді – обидві вибрані кулі будуть білі. За класичним означенням . Якщо A настала, то в урні залишилось дев’ять куль, із яких дві білі, тому . Отже, за теоремою множення .

Незалежність подій. Розглянемо тепер одне із найважливіших понять теорії ймовірностей – поняття незалежності випадкових подій. Саме це поняття виділило теорію ймовірностей із теорії міри і теорії функцій в самостійну дисципліну.

Означення 1. Події і 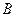називаються незалежними, якщо

.

Теорема 1.3. Для того, щоб події і 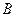були незалежними, необхідно і досить, щоб виконувалась одна із умов: (якщо ); або (якщо ).

Таким чином, незалежність подій означає, що настання однієї із подій не змінює ймовірності іншої. На практиці висновок про незалежність подій роблять на основі незалежності експериментів, із якими ці події пов’язані.

Приклад 2. Двічі підкидають монету. Нехай подія A – при першому підкиданні випадає герб, B – при другому підкиданні випадає герб. Обчислити , , , . Показати, що події A і B незалежні.

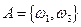Розв’язування. Простір елементарних подій складається із чотирьох рівноможливих елементарних подій: – ГГ, – ЦЦ, – ГЦ, – ЦГ. Тоді , , , а 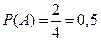, , 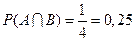. Події A і B незалежні, бо .

Умовну ймовірність знайдемо за означенням: .

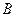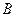Висновок про незалежність подій і можемо зробити і на основі попередньої теореми: , тому події і незалежні.

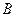Теорема 1.4. Якщо події і незалежні, то незалежними будуть і поді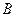ї і , і , і .

Означення 2. Події називаються попарно незалежними, якщо кожні дві – незалежні.

Означення 3. Події називаються незалежними або незалежними в сукупності, якщо для будь-якого і для будь-яких

.

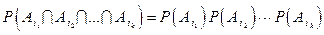Із незалежності в сукупності подій випливає їх попарна незалежність, але не навпаки.

Відзначимо також, що із того, що для деяких подій A, B, C

,

ще не випливає попарна незалежність цих подій.

Формула повної ймовірності. Формули Байєса. Нехай подія може настати із однією із подій , що утворюють повну групу і , . Це означає, що події попарно несумісні і . Тоді . Із попарної несумісності подій випливає, що події також попарно несумісні, тому . Тобто,

.