
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Послідовність незалежних випробувань. Формула Бернуллі
|
|
Нехай послідовно проводяться випадкові експерименти (випробування). Будемо вважати, що будь–яка подія, яка відноситься до фіксованого випробування, буде незалежною від будь–якої події, що відноситься до інших випробувань. Тоді говорять, що задано послідовність незалежнихвипробувань. Нехай проводиться послідовністьнезалежних випадкових експериментів, в кожному із яких може настати деяка подія  . Якщо ймовірність настання події
. Якщо ймовірність настання події 
 є однаковою в кожному експерименті, то таку послідовність випробувань називають схемою Бернуллі.
є однаковою в кожному експерименті, то таку послідовність випробувань називають схемою Бернуллі.
Нехай проводяться серії із n випробувань. Позначимо  – ймовірність того, що в
– ймовірність того, що в 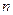 випробуваннях подія
випробуваннях подія  настане точно
настане точно 
 разів. Результати серії із n випробувань можна подати у вигляді
разів. Результати серії із n випробувань можна подати у вигляді  , де
, де  – подія, яка настає в
– подія, яка настає в 
 -му експерименті,
-му експерименті,  або
або  . Тоді
. Тоді  , якщо в
, якщо в 
 -му експерименті настала подія
-му експерименті настала подія  , і
, і  , якщо
, якщо  . Тому, враховуючи незалежність,
. Тому, враховуючи незалежність,  , а для тих
, а для тих  , у яких
, у яких  входить рівно k разів, а
входить рівно k разів, а  n–k разів
n–k разів  . Але k випробувань, у яких настає подія
. Але k випробувань, у яких настає подія  , можна вибрати
, можна вибрати 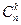 способами і для кожного з них ймовірність рівна
способами і для кожного з них ймовірність рівна  . Тоді за аксіомою адитивності,
. Тоді за аксіомою адитивності,
 . (1)
. (1)
Одержана формула називається формулою Бернуллі.
Оскільки,  , то
, то  .
.
Нехай 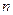 – деяке фіксоване число,
– деяке фіксоване число,  – змінне,
– змінне,  . Дослідимо поведінку
. Дослідимо поведінку  при зміні
при зміні  . Розглянемо відношення
. Розглянемо відношення
 .
.
Якщо  або
або 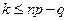 , то
, то  , тобто, ймовірності
, тобто, ймовірності 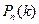 – зростають. Аналогічно,
– зростають. Аналогічно,

при  . Тому при
. Тому при  ймовірності
ймовірності 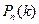 – спадають. Якщо
– спадають. Якщо  є цілим числом, то максимальне значення ймовірності
є цілим числом, то максимальне значення ймовірності  досягається при двох значеннях k, а саме:
досягається при двох значеннях k, а саме:  і
і  . Якщо ж
. Якщо ж  не є цілим числом, то максимальне значення ймовірності
не є цілим числом, то максимальне значення ймовірності  досягається тільки при одному значенні
досягається тільки при одному значенні  . Число
. Число  , при якому
, при якому  є максимальною, називається найімовірнішим числом настання події. При цьому справедлива нерівність
є максимальною, називається найімовірнішим числом настання події. При цьому справедлива нерівність
 . (2)
. (2)
Застосування формули Бернуллі при великих n вимагає великої обчислювальної роботи, при цьому виникають похибки заокруглення, тому результат одержуємо наближений. Ми розглянемо тепер деякі наближені формули, що значно спрощують обчислення ймовірностей в схемі Бернуллі.
Теорема Пуассона використовується при обчисленні ймовірностей рідких подій, коли число випробувань досить велике, а ймовірність настання події в кожному випробуванні досить мала. Таким чином, при великих n і малих p можемо використовувати наближену формулу
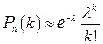 , (3)
, (3)
де  .
.
Приклад 2. Прилад містить 2000 однаково надійних елементів. Ймовірність відмови кожного із них дорівнює 0,0005. Яка ймовірність відмови приладу, якщо вона настає при відмові більше, ніж двох елементів?
Розв’язування. Нехай A – відмова більше, ніж двох елементів,  – відмова і елементів, тоді
– відмова і елементів, тоді  . Так як
. Так як  – досить велике, а
– досить велике, а  – мале, то для знаходження ймовірностей подій
– мале, то для знаходження ймовірностей подій  можемо використати наближену формулу (3), в якій
можемо використати наближену формулу (3), в якій  . Тому
. Тому

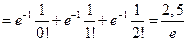 ,
,
а  .
.
При великих n обчислення ймовірностей досить громіздке, тому необхідно мати асимптотичні формули, за якими ці ймовірності можна знаходити наближено. Одну із таких наближених формул ми уже розглянули. Але, якщо ймовірність не є близькою до нуля або одиниці, то теорема Пуассона дає велику похибку. В цьому випадку вигідно застосовувати наступну теорему.
Практичне використання доведеної теореми основане на наближеній формулі
 , (10)
, (10)
де  – функція Гауса, а
– функція Гауса, а  . Значення функції Гауса можна знайти за таблицями (таблиця 1), які містяться у більшості підручників з теорії ймовірностей.
. Значення функції Гауса можна знайти за таблицями (таблиця 1), які містяться у більшості підручників з теорії ймовірностей.
Приклад 3. Ймовірність настання події в кожному із 100 незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що подія настане 90 разів.
Розв’язування. Використаємо локальну теорему Муавра-Лапласа в якій покладемо:
n = 100, p = 0,8, q = 0,2, k = 90. Тоді  , а за таблицею 1
, а за таблицею 1  . Отже, із (10) одержуємо
. Отже, із (10) одержуємо  .
.
При розв’язуванні задач часто виникає необхідність знаходити ймовірності того, що в n випробуваннях Бернуллі подія настане від до раз. За локальною граничною теоремою це робити незручно, а вигідно застосовувати наступну теорему.
Теорема. Нехай  – число появ події в
– число появ події в 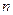 незалежних випробуваннях в кожному із яких ймовірність її настання є сталою і дорівнює p (0< p <1), то рівномірно відносно a і b
незалежних випробуваннях в кожному із яких ймовірність її настання є сталою і дорівнює p (0< p <1), то рівномірно відносно a і b  справедливе співвідношення
справедливе співвідношення
 . (11)
. (11)
Із теореми випливає, що при великих 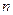 має місце наближена рівність
має місце наближена рівність
 . (21)
. (21)
Нехай  – функція Лапласа, значення якої можна знайти за таблицею 2. Таблиця складена для значень
– функція Лапласа, значення якої можна знайти за таблицею 2. Таблиця складена для значень  , а при
, а при 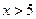 покладають
покладають 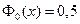 , крім того враховуємо, що
, крім того враховуємо, що  . Використовуючи рівність
. Використовуючи рівність
 ,
,
(21) можна записати у вигляді
 . (22)
. (22)
Позначимо через  – ймовірність того, що в n випробуваннях Бернуллі подія настане від
– ймовірність того, що в n випробуваннях Бернуллі подія настане від  до
до  раз. Тоді із (21) і (22) одержуємо
раз. Тоді із (21) і (22) одержуємо

або
 , (23)
, (23)
де  .
.
Приклад 4. Ймовірність настання події в кожному із 100 незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що подія настане не менше 80 і не більше 90 разів.
Розв’язування. Використаємо інтегральну теорему Муавра–Лапласа, в якій покладемо n = 100, p = 0,8, q = 0,2,  = 80,
= 80,  = 90. Тоді
= 90. Тоді  ,
,  . За таблицею 2
. За таблицею 2  (0) = 0,
(0) = 0,  (2,5) = 0,4938. Отже,
(2,5) = 0,4938. Отже, 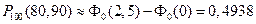 .
.
| ВИПАДКОВІ ВЕЛИЧИНИ | ||
|
Просмотров 872 |
|
|
