Одновимірні випадкові величини

Поняття події в теорії ймовірностей являє собою абстрактну модель певної якісної ознаки, що відбиває лише два альтернативні судження: є подія (відбулася) або немає (не відбулася). Подальший розвиток теорії ймовірностей потребував уведення такого нового поняття, як випадкова величина — абстрактної моделі кіль-
кісної ознаки.

1. Дискретні та неперервні випадкові величини.
Закони розподілу їх імовірностей

Розглянемо такий простір елементарних подій, в якому кожній елементарній події Ώ відповідає одне і лише одне число х або набір чисел , тобто на множині Ώ визначена певна функ­ція , яка кожній елементарній події ставить у відповідність певний елемент одновимірного простору R₁ або n-вимірного простору R_n.

Цю функцію називають випадковою величиною. У разі, коли відображає множину Ώ на одновимірний простір R₁, випадкову величину називають одновимірною. Якщо відображення здійснюється на R_n, то випадкову величину називають n-вимірною (системою n випадкових величин або n-вимірним випадковим вектором).

Отже, величина називається випадковою, якщо внаслідок проведення експерименту під впливом випадкових факторів вона набуває того чи іншого можливого числового значення з певною ймовірністю.

Якщо множина можливих значень випадкової величини є зчисленною то таку величину називають дискретною. У противному разі її називають неперервною.

Випадкові величини позначають великими літерами латинського алфавіту X, Y, Z, ... , а їх можливі значення — малими х; у; z, ... .

Для опису випадкової величини необхідно навести не лише множину можливих її значень, а й указати, з якими ймовірностями ця величина набуває того чи іншого можливого значення.

З цією метою вводять поняття закону розподілу ймовірностей.

Співвідношення, що встановляє зв’язок між можливими значеннями випадкової величини та відповідними їм імовірностями, називають законом розподілу випадкової величини.

Закон розподілу дискретної випадкової величини Х можна задати в табличній формі.

У разі табличної форми запису закону подається послідовність можливих значень випадкової величини Х, розміщених у порядку зростання, та відповідних їм імовірностей:

Оскільки випадкові події (Х = х_j) і (Х = х_m) є між собою несумісними ((Х = х_і) ∩ (Х = х_m) = Æ, і m; і, m = 1, 2, …, k) і утворюють повну групу , то необхідною є така умова:

(61)

Рівність (61) називають умовою нормування для дискретної випадкової величини Х. Наведену таблицю називають рядом розподілу.

Закон розподілу ймовірностей можна унаочнити графічно.

Для цього візьмемо систему координат р_і О х_і, відклавши на осі абсцис можливі значення випадкової величини х_і, а на осі ординат —
імовірності р_і цих можливих значень. Точки з координатами (х_і; р_і) послідовно сполучимо відрізками прямої. Утворену при цьому фігуру називають імовірнісним многокутником.

Сума ординат імовірнісного многокутника завжди дорівнює одиниці.

Функція розподілу ймовірностей
(інтегральна функція) та її властивості

Закон розподілу ймовірностей можна подати ще в одній формі, яка придатна і для дискретних, і для неперервних випадкових величин, а саме: як функцію розподілу ймовірностей випадкової величини F(х), так звану інтегральну функцію.

Функцію аргументу х, що визначає ймовірність випадкової події Х < x, називають функцією розподілу ймовірностей:

F(x) = P(X < x) (62)

Цю функцію можна тлумачити так: унаслідок експерименту випадкова величина може набути значення, меншого за х .

Розглянемо властивості F(x):

1.

2. є неспадною функцією, а саме , якщо .

Із другої властивості F(x) випливають наведені далі висновки:

1. Імовірність того, що випадкова величина Х набуде можливого значення , дорівнює приросту інтегральної функції F(x) на цьому проміжку:

(65)

2. Якщо випадкова величина Х є неперервною, то ймовірність того, що вона набуде конкретного можливого значення, завжди дорівнює нулю:

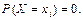
Отже, для неперервної випадкової величини Х справджуються такі рівності:

(67)