Будь-яку упорядковану підмножину, що містить m елементів з даної n-елементної множини, де m £ n, називають розміщенням з n елементів по m елементів

Із цього означення можна дійти висновку, що різні розміщення з n елементів, узятих по m, відрізняються або складом елементів, які входять до них, або порядком їхнього розташування. Наприклад, із чотирьох букв А, Б, В, Г можна утворити 12 розміщень, що містять по 2 букви:

АБ, АВ, АГ, БВ, БГ, ВГ,

БА, ВА, ГА, ВБ, ГБ, ГВ.

Іноді потрібно порахувати кількість різних розміщень з n елементів, взятих по m елементів. Наприклад, у згаданій вище задачі про вибори правління кооперативу зрозуміло, що головою може бути будь-хто із членів колективу. Отже, його можна вибрати 25 способами. Тоді для вибору його заступника, якщо вже вибрали голову, залишається 24 можливості. Тому вибір голови та його заступника разом можна здійснити 25 · 24 = 600 способами. Скарбником міг би бути хтось із решти 23 членів кооперативу. Тому існує 600 · 23 = 13800 різних способів для розв’язання цієї прозаїчної задачі.

Кількість розміщень з n елементів по m позначають символом 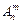(читається «а з ен по ем»).

Теорема 2.Кількість різних розміщень з n елементів по m дорівнює добутку m послідовних натуральних чисел, з яких найбільшим є n. Тобто:

■ Перший елемент m-елементної підмножини можна вибрати n способами, другий — (n – 1) способом. Упорядкована пара перших двох елементів вибирається n · (n – 1) способами. Упорядковану трійку елементів можна вибрати n × (n – 1)×(n – 2) способами. Продовжуючи ці міркування, бачимо, що ■

Виведену формулу можна записати так: . Справді,

Задача. Скільки різних трицифрових чисел можна записати за допомогою цифр 1, 2, 3, 4, 5 і 6, якщо жодна із цифр у записі будь-якого числа не буде повторюватися? Скільки таких чисел можна записати, використовуючи цифри 0, 1, 2, 3, 4, 5?

■ Зрозуміло, що в першому випадку шукане число дорівнює = 6 × 5 × 4 = 120.

Для другого випадку відповідь така: — оскільки до кількості розміщень тоді входить 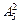розміщень, у яких цифра 0 записана на першому місці. ■

Зауважимо, що для підрахунку кількості трицифрових чисел, цифри в яких могли б повторюватися, потрібні інші міркування. Ми розглянемо їх після введення поняття розміщення з повтореннями.

Комбінації

Трапляються задачі, у яких потрібно визначити кількість різних підмножин, що містять k елементів, узятих з даної n-елементної множини. Наприклад, нехай у класі є 25 учнів і потрібно вибрати трьох учнів, яким доручається провідати хворого. При відборі такої делегації немає істотного значення, в якому порядку будуть названі імена її членів. Делегація, до складу якої входить Іван, Оля та Наталка, — та ж сама, що й делегація, до складу якої ввійшли б Оля, Іван та Наталка, якщо тільки в класі немає кількох Іванів, Наталок чи Ольг і ніхто із цих учнів не замінений на свого тезку.

Нехай маємо множину М, що містить n елементів. Будь-яка підмножина заданої множини М, яка містить k елементів, де , називається комбінацією з даних n елементів, взятих по k елементів.

Із цього означення випливає, що будь-які дві різні k-елементні комбінації відрізняються одна від одної принаймні одним елементом.

Кількість різних комбінацій з n елементів по k позначають символом 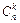(читається «це з ен по ка»).

Кожна множина має дві тривіальні підмножини: однією з них є сама множина, а іншою — порожня множина. Тому і Очевидно також, що оскільки з n елементів можна утворити лише n підмножин, кожна з містить по одному елементу.

Перед тим, як вивести формулу для обчислення 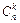покажемо, що справджується рівність:

Серед розміщень з п елементів по k можна виділити класи упорядкованих k-елементних підмножин, які відрізняються лише порядком розміщення одних і тих самих елементів. У кожному класі таких підмножин буде P_k = k!, а кількість класів — Отже, а звідси

Таким чином, ми маємо таку теорему:

Теорема 3.Кількість усіх комбінацій з п елементів, взятих по k, при виражається формулою:

За допомогою методу математичної індукції можна дати ще одне доведення цієї теореми. При k = 0 теорема істинна, оскільки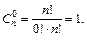

Для обґрунтування індуктивного переходу доведемо таку формулу:

З цією метою спочатку зауважимо, що з кожної (k – 1)-елементної підмножини шляхом приєднання одного з решти n – (k – 1) елементів можна утворити n – k + 1 уже k-елементних підмножин. Оскільки, далі, усіх (k – 1)-елементних підмножин є 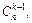а кожна з них породжує n – k + 1 k-елементних підмножин, то з усіх (k – 1)-елементних підмножин таким способом дістанемо (n – k + 1)· k-елементних підмножин. Однак слід зважити на те, що при цьому кожна k-елементна підмножина враховуватиметься k разів. Справді, підмножину a₁ a₂ a₃…а_k–1а_k, наприклад, можна утворити k різними способами:

1-й раз, якщо до підмножини а₂ а₃ … а_k–1 а_k приєднати елемент а₁;

2-й раз, якщо до підмножини а₁ а₃ … а_k–1 а_k приєднати елемент а₂;

…..............................................................................................................

нарешті, k-й раз, якщо до підмножини а₁ а₂… а_k–1 приєднати елемент а_k.

Тому

Для завершення доведення теореми 3 методом математичної індукції, припустимо, що Спираючись на це припущення та виведену формулу, маємо:

Теорему доведено.

Тепер уже легко дати відповідь до задачі, умова якої наведена на початку цього пункту. Вибір трьох учнів для відвідування хворого можна здійснити способами.