Приклади розв’язування комбінаторних задач

1. Скількома способами із 28 учнів класу можна вибрати групу для роботи в саду, якщо в групі може бути не більше 10 і не менше 4 чоловік?

■ Групу із чотирьох учнів можна вибрати способами. Інші групи — по 5, по 6, і т. д., по 10 чоловік — можна вибрати відповідно 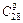і способами. За правилом додавання, маємо:

+ + + + + . ■

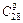2. У хорі 11 хлопчиків і 11 дівчаток. Скількома способами цих хористів
можна розмістити в ряд таким чином, щоб поряд не стояли жодні два хлопчики і жодні дві дівчинки?

■ Нехай хлопчики розміщуються на непарних місцях, а дівчатка — на парних. Існує 11! ∙ 11! = (11!)² способів такого розміщення. Крім цього, є ще стільки само способів, при яких хлопчики стоятимуть на парних місцях, а дівчатка — на непарних. Тому шукана відповідь така: 2 × (11!)². ■

3. Для військового патруля потрібно призначити 6 солдатів, 3 сержанти і два офіцери. Скількома способами це можна зробити, якщо в роті є 30 сол­датів, 6 сержантів і 4 офіцери?

Відповідь.

4. Скільки дільників має число 10¹⁰?

■ Оригінальне розв’язування цієї задачі пов’язане з розглядом добутку (1 + 2 + 2² +…+ 2⁹ + 2¹⁰) × (1 + 5 + 5² +…+ 5⁹ + 5¹⁰). Якщо просто перемножити ці многочлени, то дістанемо многочлен з 11² одночленів. Кожний із одночленів буде дільником заданого числа і всі ці числа будуть різними. Тому всіх дільників є 121.

Набагато природнішим є, однак, розв’язання, що ґрунтується на комбінаторному правилі множення. Дільниками числа 10¹⁰ = 2¹⁰ × 5¹⁰ є лише числа вигляду 2ⁿ×5^m, де п і m — цілі числа від 0 до 10. Показник n можна вибрати 11 способами. Те саме стосується й показника m. Тому всіх дільників числа 10¹⁰ є 11×11 = 121. ■

5. Для карнавального походу готують прапори. Скількома способами з п’яти сувоїв матерії різного кольору можна пошити різних прапорів, які мають по три горизонтальні смуги однакової ширини, якщо в одному прапорі жоден з кольорів не повинен повторюватися? Відповідь.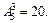

6. Скількома способами можна вибрати одну приголосну та одну голосну букву в слові математика, аби дістати різні відкриті склади?

■ Різних приголосних букв у цьому слові 3, стільки ж різних голосних. Тому потрібні вибірки можна здійснити способами. ■

7. З колоди карт, у якій є 52 різних карти, потрібно витягнути 10 карт. Скількома способами це можна зробити?

■ Такий вибір можна зробити способами. ■

7а. У скількох випадках серед вибраних карт буде хоча б один туз? У скількох випадках — чотири тузи? У скількох — лише один туз?

■ Оскільки число показує, у скількох випадках в одержаних вибірках з десяти карт не буде жодного туза, то число – характеризує випадки, коли серед вибраних карт буде хоча б один туз. Чотири тузи буде в наборах (до чотирьох тузів додається 6 карт із 48). Один туз буде в наборах. ■

8. Номер автомобільного причепа містить дві букви і чотири наступні за ними цифри. Скільки різних номерів можна скласти з 30 букв і 10 цифр?

■ Перші дві букви можна вибрати 30² способами, адже букви можуть повторюватися. Чотири цифри можна вибрати 10⁴ способами. Тому всіх різних номерних знаків може бути 30² ×10⁴ = 9 × 10⁶ = 9 000 000. ■

9. Скількома способами можна розмістити 25 різних книг у книжковій шафі, у якій є 4 полиці, якщо кожна полиця може вмістити всі 25 книг?

■ Це задача на використання поняття комбінації з повтореннями. Число, яке дорівнює визначило б кількість можливих розміщень для однакових книг. Але 25 різних книг на 25 місцях можна розмістити 25! способами. Тому всіх можливих розміщень цих книг буде ■

10. Ліфт, у якому знаходиться 9 пасажирів, може зупинятися на 10 по-верхах. Пасажири виходять групами по двоє, троє і четверо чоловік. Скількома способами це може відбутися?

■ Групу із двох чоловік можна утворити способами. Тоді групу із трьох чоловік з решта семи можна утворити способами. Третя група цілком визначиться вибором перших двох. Вибір трьох поверхів, на яких може вийти одна з груп, можливий способами. Тому загальна кількість способів, про які запитується в задачі, дорівнює (або або ). ■

11. Шість ящиків з різними матеріалами розносять по вісьмох поверхах офісу. Скількома способами можна розподілити їх по поверхах? У скількох випадках на восьмий поверх буде доставлено не менше двох ящиків?

■ Скориставшись формулою для підрахунку кількості розміщень з повтореннями із 8 елементів по 6, дістанемо перше шукане число: 8⁶. На восьмий поверх можна доставити не менше двох ящиків 8⁶ – 7⁶ – 6 × 7⁵ способами. ■

12. У класній кімнаті 6 лампочок. Скільки існує способів освітлення кімнати цими лампочками?

■ Запропонуємо два способи розв’язування цієї задачі. Підрахувавши скількома способами можна увімкнути всі 6 лампочок, 5 лампочок, і т. д., нарешті яку-небудь одну лампочку, або навіть жодної з них, дістанемо шукане число:

Той самий результат матимемо, якщо скористаємося формулою для кількості розміщень з повтореннями із двох подій (світить, не світить) на шести місцях. Відповідне число дорівнює 2⁶. ■

13. Скільки існує шестизначних телефонних номерів, у яких хоча б один раз стоять поруч цифри 2 і 5 у такому порядку?

■ Можливі п’ять випадків, при яких цифри 2 і 5 стоять поруч (див. схему):

Зрозуміло, що І і IIвипадки після заповнення усіх вільних клітин не можуть дати жодного спільного номера. Випадки І і III могли б дати 10² спільних номерів вигляду 2 5 2 5 a b , де а і b можуть бути будь-якими цифрами. Аналогічні ситуації можливі для випадків І і IV, І і V, II і ІV, II і V та III і V. Тому можливими є 6 ∙ 10²номерів, які входять одночасно до яких-небудь двож з відзначених варіантів. Може трапитися, що в І, ІІІ і V випадках з’явиться номер вигляду 2 5 2 5 2 5. Цей номер уже двічі враховувався, коли ми розглядали спільні номери для випадків І і III та III і V. Тому кількість номерів, у яких число 25 зустрічається хоча б один раз, буде 5 ∙10⁴ – 6 ×10² + 1 = 49401. ■

Формула бінома Ньютона

При розв’язуванні багатьох задач виникає потреба записати n-й степінь двочлена (бінома) a + b в розгорнутому вигляді. Ви вже знаєте, що (а + b)⁰ = 1, (а + b)¹ = а + b, (а + b)² = а² + 2ab + b², (а + b)³ = а³ + 3а²b + 3аb² + b³.Перемно­живши а + b на (а + b)³, дістанемо:

Аналогічно можна знайти (а + b)⁵, (а + b)⁶ тощо. Якщо коефіцієнти розкладу (а + b)^п при n = 0, 1, 2, … виписувати у порядку зростання показника степеня числа b, то вони утворять нескінченну трикутну таблицю:

Ця таблиця була відома ще арабським математикам у XIII ст. Вперше її властивості детально вивчив французький математик, фізик і філософ Блез Паскаль (1623 –1662). На його честь цю таблицю називають трикутником Паскаля. Умовимося рядок трикутника Паскаля, який відповідає п = 0, називати нульовим, рядок, який відповідає п = 1, — першим і т. д.

З наведеного фрагмента трикутника Паскаля можна побачити такі закономірності:

1. «Бічні сторони» трикутника Паскаля утворені одиницями.

2.Рядки симетричні відносно «висоти», тобто числа, рівновіддалені від початку і від кінця рядка, — однакові.

3. Сума двох сусідніх чисел одного рядка дорівнює числу, яке стоїть під ними в наступному рядку. Наприклад, додавши 1 і 4 з четвертого рядка, дістанемо число 5, яке стоїть під цими числами у п’ятому рядку.

Розглянемо числа:

= =1, = =3, = =3, = =1.

Звернемо увагу на те, що саме такі числа стоять у третьому рядку трикутника Паскаля. Провівши обчислення, можна переконатися, що четвертий рядок трикутника Паскаля утворюють числа Виникає припущення про те, що n-й рядок трикутника Паскаля утворюють числа

(1)

Зважимо й на те, що з тотожностей 1–3 для кількості комбінацій (див. §4) випливає, що числа 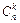мають відзначені вище властивості трикутника Паскаля. Істинність висловленого припущення випливає з наступної теореми.

Теорема. Які б не були вирази а і b та яке б не було натуральне число п, справджується така формула (формула бінома Ньютона):

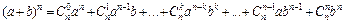. (2)

■ Доведення проведемо методом математичної індукції.

1. При n = 1 формула (2)істинна, оскільки (а + b)¹ = a + b = a + b.

2. Нехай формула (2) є істинною при n = m, тобто

Враховуючи це припущення, при n = m + 1матимемо:

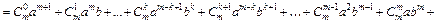
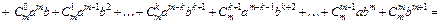
Враховуючи, крім того, що 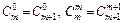і , дістанемо:

Отже, на основі принципу математичної індукції, формула (2)істинна для будь-якого натурального n. ■

Многочлен, який стоїть у правій частині формули бінома Ньютона, називається розкладом бінома. Згідно з доведеним, коефіцієнтами цього розкладу є числа Через те ці числа називають біно-міальними коефіцієнтами.

Використовуючи формулу бінома Ньютона, можна заповнити 6-й, 7-й і т. д. рядки наведеного вище фрагмента трикутника Паскаля. Зокрема, у шостому рядку стоятимуть числа отже, (a + b)⁶ = a⁶ + 6a⁵b + 15a⁴b² + 20a³b³ + 15a²b⁴ + 6ab⁵ + b⁶. Однак простіше виписати 6-й рядок трикутника Паскаля, використавши 5-ий його рядок та властивості 1–3 цього трикутника. Подумайте, як це зробити.

З доведеної теореми, як наслідки, випливають такі дві властивості біноміальних коефіцієнтів, про першу з яких уже було згадано у §4.

1. Сума всіх біноміальних коефіцієнтів для бінома степеня n дорівнює 2ⁿ.

■ Візьмемо у формулі (2) a = b = 1. Матимемо:

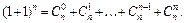
Тому ■

2. Сума біноміальних коефіцієнтів, які стоять на парних місцях, дорівнює сумі біноміальних коефіцієнтів, що стоять на непарних місцях.

■ Візьмемо у формулі (2) a = 1, b = –1. Матимемо:

тобто

(3)

Якщо n — парне, то

Якщо ж n — непарне, то ■

Той доданок у розкладі бінома (а + b)ⁿ, який містить множник b^k, називатимемо k-м членом цього розкладу і позначатимемо символом Т_k. Наприклад, є нульовим членом, — першим членом, і т. д. Тоді загальний член:

Приклад 1. Знайти член розкладу (x² + x^–3)²⁵, який не містить х.

■ Запишемо загальний член розкладу: За умовою задачі має бути: 50 – 5k = 0, звідки k = 10. Отже, десятий член розкладу не містить x. ■

Приклад 2. Сума біноміальних коефіцієнтів другого і передостаннього членів розкладу дорівнює 78. Знайти раціональні члени цього розкладу.

■ За умовою, Розв’яжемо це рівняння (з невідомим n):

Загальний член розкладу має такий вигляд:

де

Для того, аби член T_k був раціональним, необхідно і достатньо, щоб число було цілим. Це може бути лише при тих k, які діляться на 8. Оскільки то k = 0 або k = 8. Отже, раціональними членами розкладу є ■

Приклад 3. Довести тотожність

■

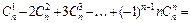
За рівністю (3) (див, стор. 35), вираз в останніх дужках дорівнює 0. Тотожність доведено. ■

Заключне зауваження

Ми розглянули найважливіші поняття комбінаторики та приклади їхнього використання для підрахунку кількості можливих вибірок, утворених за певними правилами з елементів заданої множини. Це, так би мовити, комбінаторика в «чистому вигляді». Ми зовсім не торкалися зв’язків комбінаторики з іншими розділами математики, зокрема з теорією ймовірностей, гео-метрією та математичним аналізом. Однак автори сподіваються, що уважна робота з даним посібником зацікавить читача цим цікавим розділом математики. Тоді в пригоді йому стануть інші посібники, найдоступніші з яких вказуються в кінці цієї брошури.