
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Метод по координатного спуску
|
|
Метод Симпсона.
Хай вимагається приблизно обчислити  розіб'ємо інтервал
розіб'ємо інтервал  на
на  рівних частин точками
рівних частин точками  . Хай відомі значення функції у вузлах розбиття:
. Хай відомі значення функції у вузлах розбиття:

Мал. 1.3. Геометрична інтерпретація методу Симпсона.
Як елементарне виберемо інтервал  . По трьох відомих значеннях функції будуємо многочлен Лагранжа другого порядку, використовуючи коефіцієнти Котеса; отримаємо наближену формулу:
. По трьох відомих значеннях функції будуємо многочлен Лагранжа другого порядку, використовуючи коефіцієнти Котеса; отримаємо наближену формулу:





Погрішність формули Симпсона на  визначається:
визначається:


Геометрично це означає заміну на [  ] дуги кривій
] дуги кривій  дугою параболи, що проходить через три точки
дугою параболи, що проходить через три точки  .
.
Значення визначеного інтеграла на  визначається:
визначається:

|


|
 .
.
Метод Симпсона мають п'ятий порядок точності відносно h для локальної погрішності і четвертий для глобальної.
1.5 Правило Рунге для обчислення наближеного значення погрішності.
Хай  невідоме точне значення деякої величини;
невідоме точне значення деякої величини; 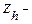 невідоме точне значення, обчислюване з кроком h, хай встановлено співвідношення:
невідоме точне значення, обчислюване з кроком h, хай встановлено співвідношення:
 (1.1)
(1.1)
де 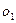 - нескінченно мала відносно
- нескінченно мала відносно  ;
;  , не залежна від
, не залежна від  ;
;  - відомі цілі значення.
- відомі цілі значення.
Позначимо через  наближене значення, знайдене з половинним кроком.
наближене значення, знайдене з половинним кроком.
 (1.2)
(1.2)
З формули (1.1) віднімемо формулу (1.2):

Виразимо 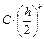

Знайдене значення підставимо у формулу (1.2), отримаємо:

Тоді наближена оцінка погрішності може бути визначений таким чином:
 .
.
1.6 Уточнене по Річардсону наближене значення.
Помножуємо формулу (1.2) на  ; з неї віднімаємо формулу (1.1):
; з неї віднімаємо формулу (1.1):


Виразимо точне значення:

Уточнене по Річардсону наближене значення визначається формулою:

Для точного значення z запишемо:

Уточнене по Річардсону значення має порядок точності  , в той час, як
, в той час, як  і
і  мають порядок точності
мають порядок точності  відносно
відносно  .
.
1.7 Застосування правила Рунге для оцінки наближеного значення визначеного інтеграла.
Хай 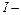 точне значення визначеного інтеграла;
точне значення визначеного інтеграла;  - наближені значення з кроками
- наближені значення з кроками  . Хай відоме співвідношення:
. Хай відоме співвідношення:

де  для формули прямокутника і трапеції;
для формули прямокутника і трапеції;
 для формули Симпсона.
для формули Симпсона.
Тоді погрішність наближеного значення визначеного інтеграла за правилом Рунге обчислюється:

Уточнене по Річардсону наближене значення рівно:

Обидві формули мають порядок точності 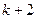 відносно
відносно  .
.
Приклад 1. 1
Знайти наближене значення визначеного інтеграла методом трапеції і Симпсона.

1. Розіб'ємо інтервал інтеграції на 4 частини з кроком  =0.25. Значення функції у вузлах розбиття занесемо в таблицю:
=0.25. Значення функції у вузлах розбиття занесемо в таблицю:
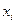
| 0.25 | 0.5 | 0.75 | ||

| 0.0624 | 0.247 | 0.533 | 0.841 |
Обчислимо наближені значення з кроком  :
:
а) Метод трапеції:


б) Метод Симпсона:


2. Розіб'ємо [0,1] на 8 частин з кроком 
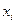
| 0,125 | 0,25 | 0,375 | 0,5 | 0,625 | 0,75 | 0,875 | ||

| 0,0156 | 0,0624 | 0,1402 | 0,247 | 0,3808 | 0,533 | 0,693 | 0,841 |
Обчислимо наближені значення з половинним кроком:

 .
.

- Оцінимо погрішність наближених значень визначеного інтеграла, обчисленого з половинним кроком:


- Обчислимо уточнені по Річардсону наближені значення:


Питання для самоперевірки
1) Як розраховуються коефіцієнти Котеса?
2) Як обчислюється інтеграл за допомогою коефіцієнтів Котеса?
3) Як визначається значення інтеграла по методу прямокутників?
4) Яка погрішність отриманого по методу прямокутників наближеного значення?
5) Як використовуються коефіцієнти Котеса для виведення формули трапеції?
6) Як визначається значення по формулі трапеції і оцінюється погрішність?
7) Як використовуються коефіцієнти Котеса при виведенні формули Симпсона?
8) Як обчислюється визначений інтеграл по методу Симпсона і оцінюється погрішність знайденого значення?
9) Яким чином обчислюється наближена погрішність значень?
10) Як обчислюється уточнене по Річардсону наближене значення?
Література, що використовується
1) [1] стор. 103-113 , стор. 118-122
2) [2] стор. 127-136 стор. 139-141
3) [3] стор. 37-49
2. ЛЕКЦІЯ 2. НАБЛИЖЕНІ МЕТОДИ ОДНОВИМІРНОЇ
МІНІМІЗАЦІЇ.
План лекції
1. Постановка задачі.
2. Метод відділення відрізків унімодальності.
3. Метод дихотомії.
4. Метод «золотого перетину».
2.1 Постановка задачі.
Задача одновимірної мінімізації полягає в знаходженні мінімального значення функції  на відрізку
на відрізку  і точки
і точки  , в якій це значення досягається. Функцію
, в якій це значення досягається. Функцію  називають функцією мети, а
називають функцією мети, а  - її точкою мінімуму.
- її точкою мінімуму.
Виз. Точка 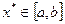 називається точкою локального мінімуму цільової функції
називається точкою локального мінімуму цільової функції  , якщо для деякого
, якщо для деякого  і довільних
і довільних  таких, що
таких, що  виконано
виконано  .
.
Виз. Функція, що має єдиний локальний мінімум на відрізку, називається унімодальною на цьому відрізку.
Процедура пошуку мінімуму складається з трьох етапів:
1) розбиття відрізка  на відрізки
на відрізки  , в кожному з яких функція
, в кожному з яких функція  унімодальна;
унімодальна;
2) уточнення точки мінімуму  на кожному відрізку
на кожному відрізку  тобто знаходження локального мінімуму із заданою точністю;
тобто знаходження локального мінімуму із заданою точністю;
3) вибір точки мінімуму  серед точок локального мінімуму шляхом виділення тієї, в якій значення функції мети якнайменше.
серед точок локального мінімуму шляхом виділення тієї, в якій значення функції мети якнайменше.
У випадку, якщо функція мети  двічі безперервно диференційована, для пошуку точок локального мінімуму можна застосовувати методи Ньютона - Рафсона, січних, дихотомії з похідними. В даній лабораторній роботі розглянуті методи, що не використовують похідних
двічі безперервно диференційована, для пошуку точок локального мінімуму можна застосовувати методи Ньютона - Рафсона, січних, дихотомії з похідними. В даній лабораторній роботі розглянуті методи, що не використовують похідних  .
.
2.2 Метод відділення відрізків унімодальності.
Служить для відділення відрізків  кожний з яких містить єдину точку локального мінімуму функції мети із заданого відрізка
кожний з яких містить єдину точку локального мінімуму функції мети із заданого відрізка  .
.
Алгоритм методу
1.Виберемо  – кількість точок розбиття
– кількість точок розбиття  . Визначимо крок
. Визначимо крок  . Побудуємо точки
. Побудуємо точки  ,
,  ,
,  .
. 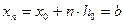 .
.
Обчислимо значення функції  в отриманих точках:
в отриманих точках:  ,
,  .
.
2. Розглянемо відрізки вигляду  для
для 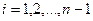 . Серед цих відрізків вибираємо такі, для яких значення
. Серед цих відрізків вибираємо такі, для яких значення  в середині відрізка не перевищує значень на його кінцях, тобто
в середині відрізка не перевищує значень на його кінцях, тобто  ,
,  . До даних відрізків приєднаємо відрізок
. До даних відрізків приєднаємо відрізок  , якщо
, якщо  і відрізок
і відрізок  , якщо
, якщо  . Кожний з виділених відрізків містить хоча б одну точку локального мінімуму. Число виділених відрізків позначимо
. Кожний з виділених відрізків містить хоча б одну точку локального мінімуму. Число виділених відрізків позначимо  .
.
3. Процедуру виділення відрізків повторюємо для 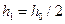 ,
,  . Якщо з деякого кроку числа виділених відрізків співпадають підряд
. Якщо з деякого кроку числа виділених відрізків співпадають підряд 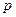 -раз, то процес відділення закінчуємо, і як відрізки унімодальності, вибираємо відрізки, виділені на останньому кроку. На практиці число
-раз, то процес відділення закінчуємо, і як відрізки унімодальності, вибираємо відрізки, виділені на останньому кроку. На практиці число  вибирається таким, щоб крок
вибирається таким, щоб крок  був у декілька разів більше заданої точності
був у декілька разів більше заданої точності  , а число
, а число 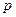 в проміжку від двох до п’яти.
в проміжку від двох до п’яти.
Приклад 2.1
1.Проведемо відділення точок локального мінімуму для функції  на відрізку
на відрізку  при
при  і
і  .
.
Обчислимо крок  . Розіб'ємо відрізок
. Розіб'ємо відрізок  точками
точками  , де
, де 

Обчислимо значення функції  в отриманих точках і занесемо в таблицю 2.1.
в отриманих точках і занесемо в таблицю 2.1.
Таблица 2.1

| |||||||
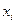
| 2.6 | 3.2 | 3.8 | 4.4 | 5.0 | 5.6 | |

| -4.808626 | -5.830948 | -4.816351 | -2.119265 | 1.318142 | 4.295084 | 5.771629 |

| |||||||
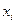
| 6.2 | 6.8 | 7.4 | 8.6 | 9.2 | ||

| 5.231979 | 2.864647 | -0.503388 | -3.695575 | -5.593792 | -5.542888 |
Розглядаємо відрізки подвійною довжини  ,
,  ,
,  , . . . Виберемо ті з них, для яких значення в середині відрізка не більш значень функцій на кінцях відрізка.
, . . . Виберемо ті з них, для яких значення в середині відрізка не більш значень функцій на кінцях відрізка.

Наприклад, для відрізка  :
:

Таких відрізків отримаємо два:  з центром в точці
з центром в точці  і
і  з центром в точці
з центром в точці  . На малюнку 2.1 ці відрізки виділені. Значить
. На малюнку 2.1 ці відрізки виділені. Значить  .
.
Проведемо ту ж процедуру з кроком  . Результати обчислень занесемо в таблицю 2.2.
. Результати обчислень занесемо в таблицю 2.2.
В даному випадку отримано також два відрізки:  з центром в точці
з центром в точці  і
і  з центром в точці
з центром в точці  .
.
Число відрізків унімодальності  .
.
Оскільки  , то закінчуємо процес відділення. Отже, отримано два відрізки унімодальності
, то закінчуємо процес відділення. Отже, отримано два відрізки унімодальності  і
і  .
.
Таблиця 2.2

| 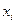
| 
| 
| 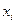
| 
|
| -4.808626 | 5.6 | 5.771629 | |||
| 2.3 | -5.568496 | 5.9 | 5.759022 | ||
| 2.6 | -5.830948 | 6.2 | 5,231979 | ||
| 2.9 | -5.572539 | 6.5 | 4.237578 | ||
| 3.2 | -4.816351 | 6.8 | 2.864647 | ||
| 3.5 | -3.629934 | 7.1 | 1.235826 | ||
| 3.8 | -2.119265 | 7.4 | -0.503388 | ||
| 4.1 | -0.419288 | 7.7 | -2.197635 | ||
| 4.4 | 1.318142 | 8.0 | -3.695575 | ||
| 4.7 | 2.937826 | 8.3 | -4.8634 | ||
| 4.295084 | 8.6 | -5.596792 | |||
| 5.3 | 5.268674 | 8.9 | -5.830239 | ||
| 9.2 | -5.542888 |
2.3 Метод дихотомії .
Методи мінімізації унімодальних функцій застосовують на кожному з отриманих інтервалів унімодальності  і служать для відшукання точок локального мінімуму
і служать для відшукання точок локального мінімуму  із заданою точністю
із заданою точністю  . Розглянемо два методи мінімізації, які не вимагають диференціювання функції мети
. Розглянемо два методи мінімізації, які не вимагають диференціювання функції мети  .
.
Метод дихотомії дозволяє на кожному кроці зменшити у двічі довжину інтервалу, що містить точку мінімуму.
Хай відрізок  є відрізком унімодальності функції
є відрізком унімодальності функції  . Розділимо його на чотири рівні частини точками:
. Розділимо його на чотири рівні частини точками:
 ,
,  ,
,  ,
, 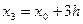 ,
,  , де
, де  . Обчислимо
. Обчислимо  ,
, 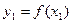 , ... .
, ... .  значення функції в цих точках.
значення функції в цих точках.
Серед точок  вибираємо точку
вибираємо точку 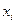 , значення функції
, значення функції  в якій якнайменше. Далі вибираємо новий інтервал. Якщо
в якій якнайменше. Далі вибираємо новий інтервал. Якщо 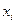 – внутрішня точка інтервалу
– внутрішня точка інтервалу  , то новий інтервал
, то новий інтервал  з центром в точці
з центром в точці 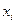 і завдовжки
і завдовжки  . У разі коли
. У разі коли  новий інтервал
новий інтервал  . Якщо ж
. Якщо ж  , тоді інтервал
, тоді інтервал  .
.
Отриманий відрізок використовується як початковий і процедура повторюється знов до тих пір, доки довжина отриманого відрізка не стане менше 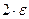 , де
, де  - задана точність. Як наближена точка локального мінімуму
- задана точність. Як наближена точка локального мінімуму  вибирається середина останнього інтервалу. Мінімальним значенням вважається значення функції в точці.
вибирається середина останнього інтервалу. Мінімальним значенням вважається значення функції в точці.
Глобальна збіжність методу для унімодальних функцій виходить з визначення. Швидкість збіжності лінійна з коефіцієнтом  щодо довжини відрізка.
щодо довжини відрізка.
Приклад 2.2
З точністю  знайти точку локального мінімуму функції
знайти точку локального мінімуму функції  на відрізку унімодальності
на відрізку унімодальності 
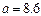 ;
; 

Розділимо початковий відрізок на чотири частини точками  ,
,  ,
,  ,
,  ,
,  .
.
Обчислимо значення даної функції в цих точках і занесемо їх в таблицю 2.3:
Таблиця 2.3

| |||||
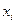
| 8.6 | 8.75 | 8.9 | 9.05 | 9.2 |

| -5.5968 | -5.7784 | -5.8302 | -5.7511 | -5.5429 |
Значення  є найменшим, на наступному кроці розглядаємо відрізок
є найменшим, на наступному кроці розглядаємо відрізок  . Його довжина рівна
. Його довжина рівна  більше
більше 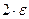 . Тому процедуру повторюємо. Обчислимо
. Тому процедуру повторюємо. Обчислимо 
Розділимо відрізок на чотири частини точками  .
.
Значення 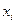 і
і  занесемо в таблицю 2.4:
занесемо в таблицю 2.4:
Таблиця 2.4

| |||||
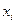
| 8.6 | 8.75 | 8.9 | 9.05 | 9.2 |

| -5.778 | -5.8207 | -5.8302 | -5.807 | -5.7511 |
 є найменшим значенням, тому новий відрізок
є найменшим значенням, тому новий відрізок  . Оскільки його довжина
. Оскільки його довжина  менше
менше  , то як точка мінімуму вибираємо
, то як точка мінімуму вибираємо  , мінімальне значення
, мінімальне значення 
2.4 Метод «золотого перетину».
Метод отримав свою назву через те, що на кожному кроці відрізок  ділиться на дві нерівні частини
ділиться на дві нерівні частини  і
і  так, щоб відношення довжини всього відрізка до довжини більшої частини дорівнювало відношенню довжини більшої частини відрізка до довжини меншої
так, щоб відношення довжини всього відрізка до довжини більшої частини дорівнювало відношенню довжини більшої частини відрізка до довжини меншої

 Такий розподіл називається «золотим перетином», число
Такий розподіл називається «золотим перетином», число  – «золотим відношенням». З вказаних пропорцій легко отримати координати точки
– «золотим відношенням». З вказаних пропорцій легко отримати координати точки  :
:

Точка  розташована на відрізку симетрично до
розташована на відрізку симетрично до  і тому
і тому

Обчислимо значення функції  в точках
в точках  і виберемо новий відрізок
і виберемо новий відрізок  таким чином:
таким чином:
- Якщо
 , то вважаємо
, то вважаємо  .
.
Тоді  стає лівою точкою “золотого перетину” відрізка
стає лівою точкою “золотого перетину” відрізка  . Для правої точки
. Для правої точки  маємо:
маємо: 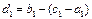
2. Якщо  , то вважаємо
, то вважаємо 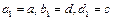 . Точка
. Точка  стає правою точкою “золотого перетину” відрізка. Для лівої точки
стає правою точкою “золотого перетину” відрізка. Для лівої точки  маємо:
маємо:  .
.

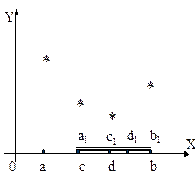
Мал. 2.2. Вибір нового відрізка методом «золотого перетину»
3. У разі, коли  порівнюємо
порівнюємо  і
і  .Якщо
.Якщо  , то відрізок
, то відрізок  вибирається як в першому випадку:
вибирається як в першому випадку:  ,
,  ,
,  ,
,  . Якщо ж
. Якщо ж  , то відрізок
, то відрізок  вибирається як в другому випадку
вибирається як в другому випадку  ,
,  ,
,  ,
,  . Процес розподілу відрізків продовжується до тих пір, доки довжина отриманого відрізка
. Процес розподілу відрізків продовжується до тих пір, доки довжина отриманого відрізка  не стане менше
не стане менше  . Як точка локального мінімуму вибирається точка
. Як точка локального мінімуму вибирається точка  .
.
Швидкість збіжності цього методу лінійна з коефіцієнтом 0,618.
Приклад 2.3. Знайти точку локального мінімуму функції  на відрізку унімодальності
на відрізку унімодальності  з точністю
з точністю  методом золотого перетину.
методом золотого перетину.
Відрізок  ділимо на три частини точками
ділимо на три частини точками



1. Обчислимо значення функції в точках  і
і 
 ;
; 
Оскільки  , тоді
, тоді  ,
,
 .Оскільки
.Оскільки  , тоді процес дроблення продовжується
, тоді процес дроблення продовжується
2.  .
.
Обчислимо  . Оскільки
. Оскільки 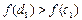 , тоді
, тоді  ;
;  ;
;  ;
;  ;
;  .
.
3.  .
.
Обчислимо  . Оскільки
. Оскільки  , тоді
, тоді
 ;
;  ;
;  ;
;  ;
; 
4.  .
.
Обчислимо  . Оскільки
. Оскільки 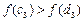 , тоді
, тоді
 ;
;  ;
;  ;
;  ;
;  .
.
5.  .
.
Обчислимо  . Оскільки
. Оскільки  , тоді
, тоді
 ;
;  ;
;  ;
;  ;
;  .Обчислимо
.Обчислимо  .
.
6. Довжина відрізка  рівна
рівна  , вона менше
, вона менше  , тому дроблення відрізків завершено.
, тому дроблення відрізків завершено.
Точка локального мінімуму  .
.
Значення функції в цій точці  .
.
Обчислення занесемо в таблицю 2.5.
Таблиця 2.5

| 
| 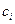
| 
| 
| 
| 
|
| 2.3 | 2.5293 | -5.8159 | 2.6707 | -5.8169 | 2.9 | |
| 2.5293 | 2.6707 | -58169 | 2.7585 | -5.7588 | 2.9 | |
| 2.5293 | 2.6172 | -5.8302 | 2.6707 | -5.7169 | 2.7586 | |
| 2.593 | 2.5828 | -5.8300 | 2.6172 | -5.8302 | 2.6707 | |
| 2.5828 | 2.6172 | -5.8302 | 2.6363 | -5.8274 | 2.6707 | |
| 2.5828 | 2.6019 | -5.8310 | 2.6172 | -5.8302 | 2.6363 | |
 =2.60955 =2.60955
| 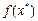 =-5.83075 =-5.83075
|
Питання для самоперевірки
1) Що називається точкою локального мінімуму функції  ?
?
2) Які етапи пошуку мінімуму?
3) Який алгоритм методу відділення відрізків унімодальності?
4) Як визначається точка мінімуму  методом дихотомії?
методом дихотомії?
5) Яке співвідношення визначає «золотий перетин»?
6) Який алгоритм методу ” золотого перетину”?
Література, що використовується
1) [4] стор. 4-19
3. ЛЕКЦІЯ 3. ГРАДІЄНТНІ МЕТОДИ МІНІМІЗАЦІЇ
ФУНКЦІЇ ДЕКІЛЬКОХ ЗМІННИХ.
План лекції
1. Постановка задачі.
2. Метод найшвидшого градієнтного спуска.
3. Метод градієнтного спуска з дробленням кроку.
4. Метод градієнтного спуска з постійним кроком.
5. Метод по координатного спуска.
3.1 Постановка задачі.
Задача багатомірної мінімізації без обмежень полягає в перебуванні точці  з
з  , у який функція мети
, у який функція мети  , має мінімальне значення. Будемо припускати, що
, має мінімальне значення. Будемо припускати, що  визначено і має безупинні частки похідні для усіх
визначено і має безупинні частки похідні для усіх  .
.
Виз. Точка 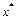 називається точкою локального мінімуму функції
називається точкою локального мінімуму функції  , якщо знайдеться
, якщо знайдеться  - окіл точки
- окіл точки  такий, що для усіх
такий, що для усіх 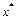 з цього околу має місце
з цього околу має місце  .
.
Точка  належить
належить  - околу точки
- околу точки 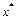 , якщо відстань
, якщо відстань  від
від  до
до 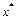 менше
менше  , тобто
, тобто

Виз. Функція, що має єдиний локальний мінімум у деякій області  , називається унімодальною на цій області.
, називається унімодальною на цій області.
Виз. Градієнтом функції F(x) називається вектор

Величина градієнта

показує найбільшу швидкість зміни функції  у точці
у точці  , а напрямок його збігається з напрямком найбільшого зростання функції. Вектор називається антиградієнтом і вказує напрямок найбільшого убування функції.
, а напрямок його збігається з напрямком найбільшого зростання функції. Вектор називається антиградієнтом і вказує напрямок найбільшого убування функції.
Точка локального мінімуму міститься в безлічі рішень системи нелінійних рівнянь 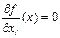 ,
,  .
.
Однак, не всі рішення системи є точками екстремум функції. Для того, щоб точка  була точкою локального мінімуму функції
була точкою локального мінімуму функції  , досить перевірити виконання наступних умов:
, досить перевірити виконання наступних умов:
1.  :
:
2. матриця Гесса в точці  позитивно визначена.
позитивно визначена.
Матрицею Гесса називається матриця розмірами  , елементами якої є частинні похідні другого порядку функції
, елементами якої є частинні похідні другого порядку функції 
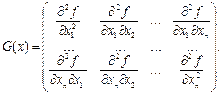
Матриця  називається позитивно визначеною, якщо всі її власні значення позитивні.
називається позитивно визначеною, якщо всі її власні значення позитивні.
Власні значення матриці А визначаються як рішення рівняння

Рівняння має  рішень
рішень 
 називають власними числами матриці
називають власними числами матриці  .
.
Пошук точок локального мінімуму можна виконати в два етапи:
1. Рішення системи лінійних рівнянь;
2. Вибір серед знайдених рішень точок локального мінімуму.
Кожний з етапів пошуку досить складний, тому на практиці найбільше часто використовуються прості ітераційні методи пошуку точок локального мінімуму. Ітераційні методи чи мінімізації методи спуска складаються в побудові послідовності
 ,
,
що сходиться до точки локального мінімуму  . Тут
. Тут  – вектор, який вказує напрямок спуска, а
– вектор, який вказує напрямок спуска, а 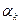 – число, що змінює довжину кроку спуска в зазначеному напрямку. Розглянемо градієнтні методи спуска. Градієнтними називають методи спуска, у яких визначається напрямком антиградієнта в точці:
– число, що змінює довжину кроку спуска в зазначеному напрямку. Розглянемо градієнтні методи спуска. Градієнтними називають методи спуска, у яких визначається напрямком антиградієнта в точці:  або
або

1. Різні градієнтні методи відрізняються лише способом вибору кроку. Тому виділимо два класи методів: методи в яких величини задані заздалегідь і не залежать від точок спуска  ;
;
2. Методи, у яких величини  обчислюються для кожної точки
обчислюються для кожної точки  .
.
Прикладом методів першого класу є метод розбіжного ряду. У ньому послідовність вибирається так, щоб виконувалися умови:
1.  при
при  ;
;
2.  (наприклад,
(наприклад,  ). Однак швидкість збіжності методу мала. До того ж класу відносяться методи градієнтного спуска з постійним кроком і з дробленням кроку, розглянуті нижче.
). Однак швидкість збіжності методу мала. До того ж класу відносяться методи градієнтного спуска з постійним кроком і з дробленням кроку, розглянуті нижче.
Найбільш відомим методом другого класу є метод найшвидшого спуска.
3.2 Метод найшвидшого градієнтного спуска.
У цьому методі  визначається так, щоб значення функції
визначається так, щоб значення функції  було найменшим з можливих значень
було найменшим з можливих значень  , тобто найменшим у напрямку
, тобто найменшим у напрямку 
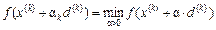 .
.
Це вимагає рішення задачі одномірної мінімізації на кожнім кроці спуска.
Алгоритм методу.
1. Нехай  . Виберемо початкову точку спуска
. Виберемо початкову точку спуска
 .
.
2. Обчислимо градієнт 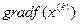 . Визначимо напрямок спуска, думаючи
. Визначимо напрямок спуска, думаючи  .
.
3. Обчислимо величину кроку  , вирішуючи задачу мінімізації функції однієї перемінної
, вирішуючи задачу мінімізації функції однієї перемінної  :
:  .
.
У якості  виберемо точку мінімуму для
виберемо точку мінімуму для  функції
функції  .
.
4. Покладемо  .
.
5. Якщо відстань
 , де
, де  – задана точність, то процес обчислень завершуємо, думаючи
– задана точність, то процес обчислень завершуємо, думаючи  ,
,  .
.
У противному випадку думаємо 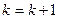 і переходимо до пункту 2.
і переходимо до пункту 2.

3.3 Метод градієнтного спуску з дробленням кроку.
У цьому методі напрямок спуска задається вектором;
 ,
,
що має одиничну довжину і напрямок антиградієнта, початковий крок покладається рівним заданій величині  . Спуск із даним кроком продовжується доти , поки значення функції при переході від
. Спуск із даним кроком продовжується доти , поки значення функції при переході від  у
у  зменшується, т. е.
зменшується, т. е. 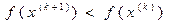 .
.
Якщо для точці  маємо
маємо  , те величина зменшується в два рази і точка
, те величина зменшується в два рази і точка  будується знову. Подальший спуск продовжується зі зменшеним кроком. Дроблення кроку продовжується доти , поки величина кроку не стане менше заданої точності:
будується знову. Подальший спуск продовжується зі зменшеним кроком. Дроблення кроку продовжується доти , поки величина кроку не стане менше заданої точності:  .
.

Алгоритм методу.
1. Покладемо  . Виберемо крок
. Виберемо крок  і початкове наближення
і початкове наближення
 .
.
Обчислимо значення функції в цій крапці  .
.
3. Обчислимо градієнт функції 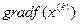 і його довжину
і його довжину  . Якщо
. Якщо  , те думаємо
, те думаємо  ,
,  і завершуємо спуск. У противному випадку
і завершуємо спуск. У противному випадку
покладемо  .
.
3. Покладемо  . Обчислимо:
. Обчислимо:  .
.
4. Порівняємо  та
та  .
.
Якщо  , та вважаємо
, та вважаємо  і перевіряємо виконання умови:
і перевіряємо виконання умови:  . Якщо нерівність вірна, то
. Якщо нерівність вірна, то  та
та  . Якщо
. Якщо  , те переходимо до пункту.3.
, те переходимо до пункту.3.
Якщо 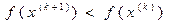 , те думаємо
, те думаємо 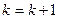 і переходимо до пункту 2.
і переходимо до пункту 2.
Приклад 3.1
Знайти точку мінімуму і мінімальне значення цільової функції 
с точністю  .
.
Точка початкового спуска 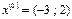 . Крок
. Крок  .
.
Рішення
Обчислимо частинні похідні:
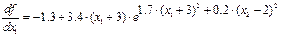

Напрямок спуска:
 ;
; 
1) 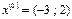 ;
;  ;
;  ;
;  .
.
Обчислимо значення функції:

Значення похідних


Довжина градієнта:

Напрямок спуска:
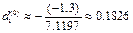


Будуємо нову точку:
2)

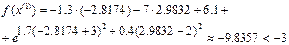
Значення функції зменшилося.
Обчислимо частинну похідну в точці  :
:


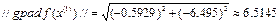
Напрямок спуска:



3)


Значення функції зменшилося.
Обчислимо частинні похідні в точці  :
:



Напрямок спуска:



4)
|
Просмотров 612 |
|
|


