Задача 4. Найдите все непрерывные функции удовлетворяющие условию

Задача 1. Найдите все функции, определённые на , удовлетворяющие условию .

Пусть - некоторое действительное число. Тогда или . Отсюда или . Из этого видно, что, если функции существуют, то их графикам будут принадлежать точки или . Понятно, что такими функциями будут функции и , но не только они!!! Например, функция также является решением уравнения.

Решением будет являться и функция

Это знаменитая функция Дирихле

Можно сконструировать ещё несколько функций-решений данного функционального уравнения.

Окончательный ответ будет звучать так:

- всякая, определённая на функция, график которой принадлежит объединению двух прямых 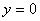и .

Задача 2. Найдите функцию , определённую на множестве натуральных чисел, удовлетворяющую условию , где - некоторое действительное число.

Будем решать это уравнение по схеме, которая в математике называется методом Коши.

1. Найдём выражения для Получим , , .

2. Этот “эксперимент” подсказывает, что , где .

3. Проверим, действительно ли выполняется равенство , где . Применим для доказательства метод математической индукции.

1. Проверим, выполняется ли равенство при : - верно.

2. Предположим, что равенство верно при , где , т.е. - верно.

3. Докажем, что из этого следует равенство для . Т.к. , то при получим или ; . Значит, равенство верно для любого натурального 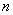. Таким образом, решением заданного функционального уравнения будет функция , где - произвольное число.

Надеюсь, Вы узнали в этой функции давнюю знакомую – бесконечную арифметическую прогрессию.

Попробуйте сами составить функциональное уравнение, решением которого будет геометрическая прогрессия. Если не сможете, не огорчайтесь, попробуйте “увидеть” это уравнение в одной из задач для самостоятельной работы.

Рассмотрим ещё один метод решения функциональных уравнений – метод подстановки. Он заключается в подстановке вместо переменных их некоторых значений, позволяющих найти функцию .

Задача 3. Найдите все функции, определённые на множестве , удовлетворяющие соотношению .

Придадим значение . Получим .

Отсюда .

Получим систему

Из уравнения (1) выразим и подставим в уравнение (2).

; ;

Отсюда ; ; .

Проверим, действительно ли функция удовлетворяет уравнению .

- верно.

Ответ: .

Решим ещё одно функциональное уравнение методом Коши.

Задача 4. Найдите все непрерывные функции удовлетворяющие условию .

Будем находить решение функционального уравнения постепенно, т.е. сначала найдём его решение, если 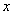является натуральным числом, затем – целым, потом рациональным и, наконец, - действительным.

1. Пусть . Тогда .

2. При , получим , ,

3. Докажем методом математической индукции, что при натуральных значениях 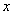(докажите это самостоятельно!) . (1)

4. При получим . - постоянное число. Обозначим его через . Значит, для , имеем .

5. Положим в равенстве (1) , где , получим . Отсюда или . Обозначив через , получим . Значит, при положительном и рациональном 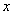мы получим . Предполагая, что функция - непрерывна, получим , при , .

6. Возьмём в равенстве 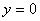. Получим . Отсюда .

7. Возьмём в этом равенстве . Получим или .

Т.к. , то , т.е. . Итак, для любого действительного 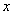решением уравнения будет функция .

Ответ:

Замечание. Уравнение называется уравнением Коши.

Ещё один способ решения функциональных уравнений заключается в использовании функциональных уравнений с известным решением.

Задача 5. Найдите непрерывные функции , удовлетворяющие условию . (1)

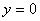Попробуем свести это уравнение к функциональному уравнению Коши с непрерывным решением . Пусть , тогда . Так как - постоянное число, обозначим его через и получим .

Придадим теперь 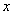значение . Получим . Из уравнения (1) получим или (2). Решением уравнения (1) является функция . Значит, решением уравнения (2) будет функция .

Ответ: .