Класифікація на основі байєсовської теорії рішень

Байєсовський підхід

Байєсовський підхід виходить із статистичної природи спостережень. За основу береться припущення про існування імовірнісної міри на просторі образів, яка або відома, або може бути оцінена. Мета полягає в розробці такого класифікатора, який буде правильно визначати найбільш вірогідний клас для пробного образу. Тоді задача полягає у визначенні "найбільш вірогідного" класу.

Задано M класів Ω¹, Ω², …, Ω^M, а також P(Ω^і │x), i = 1,2,.., M - вірогідність того, що невідомий образ, що представляється вектором ознак x, належить класу Ω^і.

P(Ω^і │x)називається апостеріорною вірогідністю, оскільки задає розподіл індексу класу після експерименту (a posteriori - тобто після того, як значення вектора ознак x було отримано).

Розглянемо випадок двох класів Ω¹і Ω². Природно вибрати вирішальне правило таким чином: об'єкт відносимо до того класу, для якого апостеріорна вірогідність вища. Таке правило класифікації за максимумом апостеріорної вірогідності називається Байєсовським: якщо P(Ω¹ │x)> P(Ω² │x), то x класифікується в Ω¹, інакше в Ω². Таким чином, для вирішального Байєсовського правила необхідно отримати апостеріорну вірогідність P(Ω^і │x), i = 1,2 . Це можна зробити за допомогою формули Байеса.

Формула Байеса, отримана Т. Байесом в 1763 році, дозволяє вичислити апостеріорну вірогідність подій через апріорну вірогідність і функції правдоподібності.

Нехай A₁, A₂,.., A_n - повна група несумісних подій. A_i = Ω. A_i A_j = Ø при i ≠ j. Тоді апостеріорна вірогідність має вигляд:

P(A_і │B) =

Де P(A_і )─ апріорна вірогідність події A_і, P(B│A_і )─ умовна вірогідність події Bза умови, що сталася подія A_і.

Розглянемо отримання апостеріорної вірогідності P(Ω │x), знаючи P(Ω)і P(x │Ω).

P(AB) = P(A│B) P(B), P(AB) = P(B│A) P(A) P(A│B) P(B) = P(B│A) P(A)

P(B│A) =

Якщо P(A)і P(A│B)описуються щільностями p(x)і p(x|B), то

P(B│х) = ═> P(Ω_і│х) =

При перевірці класифікації порівняння P(Ω₁│x)і P(Ω₂│x)еквівалентне порівнянню р(х│Ω₁)P(Ω₁)і р(х│Ω₂)P(Ω₂).

У разі, коли P(Ω₁│x) = P(Ω₂│x), вважається, що міра множини x дорівнює нулю.

Таким чином, задача порівняння по апостеріорній вірогідності зводиться до обчислення величин P(Ω₁), P(Ω₂), р(х│Ω₁)і р(х│Ω₂). Будемо вважати, що у нас достатньо даних для визначення вірогідності приналежності об'єкта кожному з класів P(Ω_і), і = 1,2. Такі вірогідності називаються апріорними вірогідностями класів. Також будемо вважати, що відомі функції розподілу вектора ознак для кожного класу P(Ω_і│x),і = 1,2. Вони називаються функціями правдоподібності х по відношенню до Ω_і. Якщо апріорна вірогідність і функції правдоподібності невідомі, то їх можна оцінити методами математичної статистики на множині прецедентів.

Наприклад, P(Ω_і) ≈ ,де N_і ─ кількість прецедентів з Ω_{і ,} і = 1,2. N - загальне кількість прецедентів. Р(х|Ω_і.) може бути наближене гістограмою розподілу вектора ознак для прецедентів з класу Ω_і.

Отже Байєсовський, підхід до статистичних задач грунтується на припущенні про існування деякого розподілу вірогідності для кожного параметра. Недоліком цього методу є необхідність відповідного постулату як існування апріорного розподілу для невідомого параметра, так і знання його форми.

Помилка класифікації

Вірогідність називається помилкою класифікації,

R₁= {x: P(Ω₁)р(х│Ω₁) > P(Ω₂)р(х│Ω₂)} R₂= {x: P(Ω₁)р(х│Ω₁) < P(Ω₂)}

області рішення (Ω₁ Ω₂ = Ø).

Теорема. Байєсовський класифікатор є оптимальним по відношенню до мінімізації вірогідності помилки класифікації.

Доведення. Розглянемо помилку класифікації :

Р_е = Р(х R₂, Ω₁) + Р(х R₁, Ω₂)= P(Ω₁) 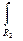р(х│Ω₁)dx + P(Ω₂) р(х│Ω₂)dx=

= P(Ω₁) (1 - р(х│Ω₁)dx) + P(Ω₂) р(х│Ω₂)dx= P(Ω₁) - P(Ω₁) р(х│Ω₁)dx + P(Ω₂) р(х│Ω₂)dx

Враховуючи формулу Байєса: P(Ω_і│х) = ,і = 1,2 отримаємо:

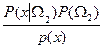= P(Ω₁) - P(Ω₁) Р dx + P(Ω₂) Р dx =

= P(Ω₁) - P(Ω₁│х)p(x)dx + P(Ω₂│х)p(x)dx= P(Ω₁) - p(x) (P(Ω₁│х) - P(Ω₂│х))dx

Таким чином, мінімум досягається, коли R₁ = {х: (P(Ω₁│х)> P(Ω₂│х)}. R₂ вибирається з інших точок.

Ця теорема була доведена для двох класів Ω₁ і Ω₂. Узагальнимо її на M класів.

Нехай вектор ознак x відноситься до класу Ω_і, якщо (P(Ω_і│х)> P(Ω_j│х), при i ≠ j, i = 1,2,.., M, j = 1,2,.., M. Необхідно довести, що це правило мінімізує вірогідність помилки класифікації. Для доведення слід cкористатися формулою правильної класифікації Р_r = 1 - Р_е.

Доведення. Скористаємося формулою правильної класифікації Р_r = 1 - Р_е.

Р_r = Р(х R₁, Ω₁) + Р(х R₂, Ω₂ ) +… + Р(х R_l, Ω_l )=

= Р(х R_i│ Ω_i) P(Ω_i)= P(Ω_i) p(x│ Ω_i) dx =

= P(Ω₁) (1- p(x│ Ω_i) dx) + P(Ω_i) p(x│ Ω_i) dx)=

= P(Ω₁) - ( P(Ω₁) p(x│ Ω_i) dx - P(Ω_i) p(x│ Ω_i) dx)=

Враховуючи формулу Байєса при i=1,2,…l, отримаємо:

= P(Ω₁) - ( P(Ω₁) dx - dx) =

= P(Ω₁) - ( P(Ω₁│x) p(x) dx - P(Ω_i│x) p(x) dx)

P(Ω1) - ( p(x) (P(Ω1│x) - P(Ωi│x)) dx

Таким чином, максимум досягається, коли Р(ω_l│х)< Р(ω_i│х). Аналогічно для всіх j = 1,2,..,l максимум досягається, коли R_i = {х: Р(ω_j│х)< Р(ω_i│х) }.