Расчет трубопровода с непрерывным изменением расхода по длине

Часто встречаются случаи, когда по длине трубопровода происходит раздача некоторой части расхода или всего расхода, причем отбор жидкости (воды) потребителями происходит в нескольких сечениях по длине трубопровода.

К таким трубопроводам относятся городские и сельские водопроводы,

дренажные коллекторы работают в условиях увеличения расхода по длине.

Рассмотрим случай, когда жидкость (вода) забирается из трубопровода равномерно по его длине. Обозначим через q расход, отдаваемый трубой на сторону с одной единицы ее длины. Очевидно, что при равномерной отдаче воды на сторону расход в трубе Q уменьшается по линейному закону. Имея это в виду, эпюру расходов воды в самой трубе можно представить трапецией: правая крайняя ордината этой эпюры выражает транзитный расход Qт; левая крайняя ордината этой эпюры выражает расход в начальном сечении трубы, этот расход равен Qт + ql . Потерю напора для трубы, имеющий переменный по длине расход определяют по выражению:

В случае отсутствия транзитного расхода (Qт = 0) расчетный расход определяется:

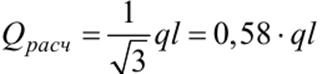
При наличии транзитного расхода (Qт ≠ 0) расчетный расход находят по следующей приближенной формуле:

Сифонный трубопровод

Сифоном называется самотечная труба, часть которой расположена выше горизонта жидкости в сосуде, который ее питает.

Ограничимся рассмотрением истечения жидкости из сифона под уровень.

Если трубу заполнить жидкостью, то после этого начнется движение жидкости из верхнего сосуда в нижний. Жидкость в такой трубе будет двигаться. Наметим сечение трубы n-n и обозначим превышение его над горизонтом жидкости: в левом сосуде – через h' и в правом сосуде – через h''. Если предположить, что жидкость, заполняющая сифон, находится в покое, то можем написать:

а) давление в сечении n-n с левой стороны: б) давление в сечении n-n с правой стороны: где (– h') и (– h'') – соответствующие заглубления сечения n-n под горизонтом жидкости в сосудах. Как видно, р1 > р2. отсюда понятно, что жидкость в трубе не может находиться в покое: она будет двигаться в сторону меньшего давления. Рассмотрим установившееся движение жидкости в сифоне. Наметим два сечения: 1-1 и 3-3. Соединяя эти сечения уравнением Бернулли, получим формулу для расхода Q в трубе в виде зависимости:

Характерным для сифона является то, что в нем вакуум. Наибольшая величина вакуума будет в сечении n-n, наиболее высоко расположенном. Найдем максимальную величину вакуума в сифоне. Наметим по линии n-n, где ищем вакуум, сечение 2-2 и затем соединим сечения 1-1 и 2-2 уравнением Бернулли (плоскость сравнения проведем на уровне горизонта жидкости в левом сосуде):

где z1 = 0; z2 = h';

где υ – скорость в трубе; рn – давление в n-n .

Потери напора hпот на пути от сечения 1-1 до сечения 2-2 выражаем через формулу Дарси – Вейсбаха: где l – длина трубы сифона от сечения 1-1 до сечения 2-2.

Запишем уравнение Бернулли с учетом выше сформулированных условий:

.
Так как , то (1). Из формулы (1) видно, что зависит от h'; если h' будет велико, то и будет велико. При больших струя в сифоне может разорваться, и сифон перестанет работать. Считают, что для нормальной работы сифона величина должна быть такой, при которой удовлетворяется условие: ,где – вакуум, допустимый по условиям невозможности образования разрыва турбулентной струи. Величину для воды (при нормальном атмосферном давлении) можно принять равной:

м вод. ст. Анализируя вопрос о разрыве струи в сифоне, надо учитывать следующие обстоятельства.

1. В сифоне из жидкости должен выделяться растворенный воздух (в связи с уменьшением давления в районе сечения n-n). Этот воздух скапливается в виде воздушного «мешка» в верхней точке сечения n-n. Выпуск его через какой-либо клапан невозможен: при открытии клапана в районе сечения n-n атмосферный воздух будет поступать в трубу, увеличивая воздушный «мешок». Этот «мешок» может быть удален из сифона только при помощи особого насоса.

2. При достаточно большей величине h' движение жидкости в сифоне представляют по схеме на рис.а: наибольший объем кавитационных паровоздушных областей имеет место в сечении n-n. По мере движения жидкости от сечения n-n к выходу эти кавитационные области, увлекаемые потоком, закрываются и постепенно исчезают.