
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Пример выполнения курсового задания С 1
|
|
 |
На рис. 1.49 изображена расчётная схема балки.
Дано: P = 20 кН; M = 10 кН·м; q = 2 кНм. Определить реакции внешних связей в точках А и В.
Решение.
Определение реакций внешних связей для рассматриваемой балки проводится согласно алгоритму решения задач статики, приведённому в подразделе 1.7.
1. Выбирается система отсчёта. Так как балка плоская, то выбирается система отсчёта OXY.
2. Выделяется тело, равновесие которого рассматривается. В нашем случае таким телом является балка, изображённая на рис. 1.49.
3. К балке прикладываются активные нагрузки. По условию задачи активные нагрузки известны. Так как задана распределённая нагрузка с интенсивностью q, то её приводят к сосредоточенной силе Q, модуль которой определяют по формуле Q = q×L = 2×2 = 4 кН. Эту сосредоточенную силу прикладывают к телу и показывают размер, на котором она приложена. Таким образом, на балку действуют следующие активные нагрузки: P, Q – активные силы; активная пара сил с алгебраическим моментом М.
4. Согласно аксиоме связей внешние связи, наложенные на механическую систему в точках А и В, отбрасывают и показывают реакции внешних связей XA, YA, RB. Таким образом, на балку действуют внешние нагрузки, состоящие из активных нагрузок: P, Q, M и реакций внешних связей: XA, YA, RB.
5. Так как система внешних сил, действующих на тело, является плоской и произвольной, то записывают три уравнения равновесия:
Σ  + Σ
+ Σ 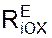 = 0 = Q – P·cos(60о) + XA = 0; (1)
= 0 = Q – P·cos(60о) + XA = 0; (1)
Σ  + Σ
+ Σ  = 0 = – P·sin(60о) + RB + YA = 0; (2)
= 0 = – P·sin(60о) + RB + YA = 0; (2)
Σ MA(FiE) + Σ MA(RiE) = 0 =
= M + P·sin(600)×2 – P·cos(60о)·1 – RB×4 = 0. (3)
При составлении выражений (1), (2), (3) использована первая форма уравнений равновесия. Эти уравнения решают в наиболее удобной последовательности и находят проекции неизвестных реакций на координатные оси системы отсчёта OXY или модули этих реакций.
Из уравнения (1) XA= – Q + P·cos(60о) = – 4 + 20×0,5 = 6,000 кН.
Из уравнения (3) RB = (M + P·sin(60о)×2 – P·cos(60о)×1)4 =
= (10 + 20×0,866×2 – 20×0,5×1)4 = 8,660 кН.
Из уравнения (2)
YA= – RB + P·sin(60о) = – 8,66 +20×0,866 = 8,660 кН.
 |
Согласно условию задания необходимо произвести проверку правильности проведённых расчётов. С целью такой проверки изобразим рассматриваемую балку в упрощённом варианте (рис. 1.50).
Сила Р разложена на составляющие силы по координатным осям. Это упрощает проецирование силы Р на координатные оси системы отсчёта OXY. Необходимо отметить, что силы раскладываются на составляющие по координатным осям системы отсчёта только в точке их приложения. Порядок решения задачи остается прежним, только использована третья форма уравнений равновесия.
Σ MС(FiE) + Σ MС(RiE) = 0 =
= M – Q·1 – RB·2 + YA·2 – XA·1 = 0; (4)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= M – Q·1 + P·sin(60о)·2 – RB·4 – XA·1 = 0; (5)
Σ MЕ(FiE) + Σ MЕ(RiE) = 0 =
= M – P·sin(600)·2 – P·cos(60о)·1 + YA·4 = 0. (6)
Подставляя найденные значения реакций XA, YA, RB в выражения (4), (5), (6) и вычислив, получим:
Σ MС(FiE) + Σ MС(RiE) = 0 =
= 10 – 4·1 – 8,660·2 + 8,660·2 – 6·1 = 0; (4I)
Σ MD(FiE) + Σ MD(RiE) = 0 =
= 10 – 4·1 + 20·0,866·2 – 8,660·4 – 6·1 = 0; (5I)
Σ MЕ(FiE) + Σ MЕ(RiE) = 0 =
= 10 – 20·0,866·2 – 20·0,5·1 + 8,660·4 = 0. (6I)
Проведённая проверка подтвердила правильность результатов расчётов. Результаты вычислений помещают в таблицу.
Таблица
|
Просмотров 1050 |
|
|
