Статическая детерминированная модель без дефицита

Статическая детерминированная модель без дефицита

Предположение о том, что дефицит не допускается, означает полное удовлетворение спроса на запасаемый продукт, т.е. совпадение функций r(t) и b(t). Пусть общее потребление запасаемого продукта за рассматриваемый интервал времени равно N. Рассмотрим простейшую модель, в которой предполагается, что расходование запаса происходит непрерывно с постоянной интенсивностью, т.е. b(t)=b. Эту интенсивность можно найти, разделив общее потребление продукта на время, в течение которого он расходуется:

(2.3)

Пополнение заказа происходит партиями одинакового объема, т.е. функция a(t) не является непрерывной: a(t)=0 при всех t, кроме моментов поставки продукта, когда a(t)=n, где n — объем партии. Так как интенсивность расхода равна b, то вся партия будет использована за время

(2.4)

Рис. 7 Рис. 8

Если отсчет времени начать с момента поступления первой партии, то уровень запаса в начальный момент равен объему этой партии n, т.е. J(0)=n. Графически уровень запаса в зависимости от времени представлен на рис. 7.

На временном интервале [0, T] уровень запаса уменьшается по прямой от значения n до нуля. Так как дефицит не допускается, то в момент T уровень запаса мгновенно пополняется до прежнего значения n за счет поступления партии заказа. И так процесс изменения J(t) повторяется на каждом временном интервале продолжительностью Т (см. рис. 7).

Задача управления запасами состоит в определении такого объема партии n, при котором суммарные затраты на создание и хранение запаса были бы минимальными.

Обозначим суммарные затраты через С, затраты на создание запаса — через С₁, затраты на хранение запаса — через С₂ и найдем эти величины за весь промежуток времени Т.

Пусть затраты на доставку одной партии продукта, не зависимые от объема партии, равны с₁, а затраты на хранение одной единицы продукта в единицу времени — с₂. Так как за время необходимо запастись N единицами продукта, который доставляется партиями объема n, то число таких партий k равно:

(2.5)

Отсюда получаем (2.6)

Мгновенные затраты хранения запаса в момент времени t равны c₂J(t). Значит, за промежуток времени [0, Т] они составят или, учитывая (2.4):

Средний запас за промежуток [0, Т] равен nТ/2, т.е. затраты на хранение всего запаса при линейном (по времени) его расходе равны затратам на хранение среднего запаса.

Учитывая периодичность функции J(t) (всего за промежуток времени будет «зубцов», аналогичных рассмотренному на отрезке [0, Т]), и формулу (2.5), получаем, что затраты хранения запаса за промежуток времени равны:

(2.7)

Нетрудно заметить, что затраты С₁ обратно пропорциональны, а затраты С₂ прямо пропорциональны объему партии n. Графики функций С₁(n) и С₂(n), а также функции суммарных затрат

(2.8)

приведены на рис. 8.

В точке минимума функции С(n) ее производная

, откуда

(2.9)

или, учитывая (2.3):

(2.10)

Формула (2.10), называемая формулой Уилсона или формулой наиболее экономичного объема партии, широко используется в экономике. Эта формула может быть получена и другим способом, если учесть, что произведение 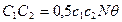есть величина постоянная, не зависящая от n. В этом случае, как известно, сумма двух величин принимает наименьшее значение, когда они равны, т. е. С₁ =C₂ или

(2.11)

откуда получаем (2.9).

Из (2.11) следует, что минимум общих затрат задачи управления запасами достигается, когда затраты на создание запаса равны затратам на хранение запаса. При этом минимальные суммарные затраты

(2.12)

откуда, учитывая (2.9) и (2.3), получим

или (2.13)

Число оптимальных партий за время с учетом (2.5), (2.9) и (2.3) равно:

Время расхода оптимальной партии на основании (2.4) с учетом (2.9) и (2.3) равно (2.14)

или (2.15)