Доверительные интервалы для оценки среднего квадратического отклонения нормального распределения

Будем искать для среднего квадратического отклонения нормально распределенной случайной величины доверительный интервал вида (s – δ, s +δ), где s – исправленное выборочное среднее квадратическое отклонение, а для δ выполняется условие: p ( |σ – s| < δ ) = γ.

Запишем это неравенство в виде: или, обозначив ,

. (18.4)

Рассмотрим случайную величину χ, определяемую по формуле

,

которая распределена по закону «хи-квадрат» с п-1 степенями свободы (см. лекцию 12). Плотность ее распределения

не зависит от оцениваемого параметра σ, а зависит только от объема выборки п. Преобразуем неравенство (18.4) так, чтобы оно приняло вид χ1 < χ < χ2. Вероятность выполнения этого неравенства равна доверительной вероятности γ, следовательно, Предполо-жим, что q < 1, тогда неравенство (18.4) можно записать так:

,

или, после умножения на , . Следовательно, . Тогда Существуют таблицы для распределения «хи-квадрат», из которых можно найти q по заданным п и γ, не решая этого уравнения. Таким образом, вычислив по выборке значение sи определив по таблице значение q, можно найти доверительный интервал (18.4), в который значение σ попадает с заданной вероятностью γ.

Замечание. Если q > 1, то с учетом условия σ > 0 доверительный интервал для σ будет иметь границы

. (18.5)

Пример.

Пусть п = 20, s = 1,3. Найдем доверительный интервал для σ при заданной надежности γ = 0,95. Из соответствующей таблицы находим q (n = 20, γ = 0,95 ) = 0,37. Следовательно, границы доверительного интервала: 1,3(1-0,37) = 0,819 и 1,3(1+0,37) = 1,781. Итак, 0,819 < σ < 1,781 с вероятностью 0,95.

Доверительный интервал для математического ожидания нормальной величины при известном среднеквадратическом отклонении .

Пусть выборка, полученная из нормальной генеральной совокупности с известным среднеквадратичным отклонением . Требуется построить доверительный интервал для параметра , соответствующий доверительной вероятности .

Так как каждая из величин распределена по закону , то выборочное среднее распределено также нормально с параметрами , . Тогда .

Найдем и , для которых 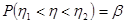. Так как распределение симметрично, то разумно взять , где - квантиль распределения порядка (рис). Тогда:

,

или (3.1)

или , где

Замечание 1. Если для нахождения квантилей используется функция Лапласа 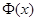, то следует использовать соотношение: .

Пример. Найти доверительный интервал для математического ожидания нормальной случайной величины 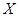с надежностью , если , , .

Решение. Имеем 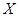- нормальная случайная величина с известным . Требуется построить доверительный интервал для математического ожидания этой величины, то есть для параметра . По таблицам функции Лапласа находим , для которого . Следовательно, . Таким образом, с вероятностью :

или .

Замечание 2. Если значение неизвестно, то с помощью статистики невозможно построить точный доверительный интервал для параметра нормальной случайной величины. Однако, при больших величину можно заменить состоятельной оценкой) (или ), построив статистику . Так как , то 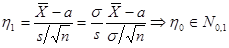, то есть статистику можно использовать для построения АДИ для параметра . Тогда, если , - квантили распределения то: 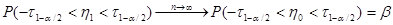и искомый интервал имеет вид: .

Кроме того, поскольку, в соответствии с центральной предельной теоремой, величина распределена асимптотически нормально для любой случайной величины , имеющей конечные математическое ожидание и дисперсию, при больших эту величину можно использовать для построения асимптотических доверительных интервалов для математического ожидания при любом законе распределения величины . Если же неизвестна величина , то при больших ее можно заменить состоятельными оценками или .

Замечание 3. Функция не годится для построения доверительного интервала для нормальной случайной величины при известном параметре , а тем более при неизвестном а. Действительно, разрешая неравенство относительно , мы получим (при условии ) - бесконечный доверительный интервал.