
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Глава 12. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
|
|
Определить, какие из точек M1(3; 1), M2(2; 3), M3(6; 3), M4(-3; -3), M5(3; -1), M6(-2; 1) лежат на прямой  и какие на ней не лежат. и какие на ней не лежат.
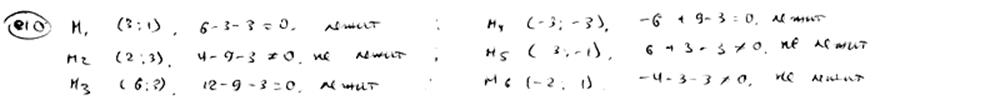
| ||
Точки P1, P2, P3, P4, P5 расположены на прямой  ; их абсциссы соответственно равны числам 4; 0; 2; -2; -6. Определить ординаты этих точек. ; их абсциссы соответственно равны числам 4; 0; 2; -2; -6. Определить ординаты этих точек.
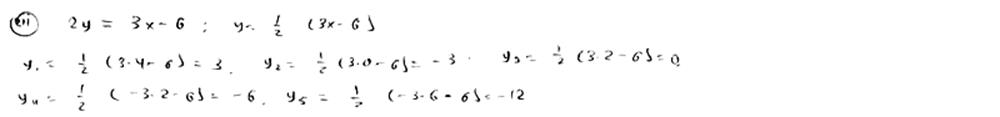
| ||
Точки Q1, Q2, Q3, Q4, Q5 расположены на прямой  ; их ординаты соответственно равны числам 1; 0; 2; -1, 3. Определить абсциссы этих точек. ; их ординаты соответственно равны числам 1; 0; 2; -1, 3. Определить абсциссы этих точек.

| ||
Определить точки пересечения прямой  с координатными осями и построить эту прямую на чертеже. с координатными осями и построить эту прямую на чертеже.

| ||
Найти точку пересечения двух прямых 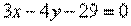 , , 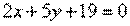 . .

| ||
Стороны АВ, ВС и АС треугольника АВС даны соответственно уравнениями  , ,  , ,  . Определить координаты его вершин. . Определить координаты его вершин.

| ||
Даны уравнения двух сторон параллелограмма  , ,  и уравнение одной из его диагоналей и уравнение одной из его диагоналей  . Определить координаты вершин этого параллелограмма. . Определить координаты вершин этого параллелограмма.

| ||
Стороны треугольника лежат на прямых  , ,  , ,  . Вычислить его площадь S. . Вычислить его площадь S.

| ||
Площадь треугольника S=8, две его вершины суть точки А(1; -2), В(2; 3), а третья вершина С лежит на прямой  . Определить координаты вершины С. . Определить координаты вершины С.

| ||
Площадь треугольника S=1,5, две его вершины суть точки А(2; -3), В(3; -2), центр масс этого треугольника лежит на прямой  . Определить координаты третьей вершины С. . Определить координаты третьей вершины С.

| ||
| Составить уравнение прямой и построить прямую на чертеже, зная ее угловой коэффициент k и отрезок b, отсекаемый ею на оси Oy: | ||
| 220.1 | k=2/3, b=3; | |
| 220.2 | k=3, b=0; | |
| 220.3 | k=0, b=-2; | |
| 220.4 | k=-3/4, b=3; | |
| 220.5 | k=-2, b=-5; | |
| 220.6 | k=-1/3, b=2/3.

| |
| Определить угловой коэффициент k и отрезок b, отсекаемый на оси Oy, для каждой из прямых: | ||
| 221.1 |  ; ;
| |
| 221.2 |  ; ;
| |
| 221.3 |  ; ;
| |
| 221.4 |  ; ;
| |
| 221.5 | 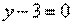 . .

| |
Дана прямая  . Определить угловой коэффициент k прямой: . Определить угловой коэффициент k прямой:
| ||
| 222.1 | Параллельной данной прямой; | |
| 222.2 | Перпендикулярно к данной прямой.

| |
Дана прямая  . Составить уравнение прямой, проходящей через точку М0(2; 1): . Составить уравнение прямой, проходящей через точку М0(2; 1):
| ||
| 223.1 | Параллельно данной прямой; | |
| 223.2 | Перпендикулярно данной прямой.

| |
Даны уравнения двух сторон прямоугольника  , ,  и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого прямоугольника. и одна из его вершин А(2; -3). Составить уравнения двух других сторон этого прямоугольника.

| ||
Даны уравнения двух сторон прямоугольника  , ,  и уравнение одной из его диагоналей и уравнение одной из его диагоналей  . Найти вершины прямоугольника. . Найти вершины прямоугольника.

| ||
Найти проекцию точке Р(-5; 13) относительно прямой  . .

| ||
Найти точку Q, симметричную точке Р(-5; 13) относительно прямой  . .

| ||
| В каждом из следующих случаев составить уравнение прямой, параллельной двум данным прямым и проходящей посередине между ними: | ||
| 228.1 |  , ,  ; ;
| |
| 228.2 |  , ,  ; ;
| |
| 228.3 |  , ,  ; ;
| |
| 228.4 |  , ,  ; ;
| |
| 228.5 |  , ,  . .

| |
| Вычислить угловой коэффициент k прямой, проходящей через две данные точки: | ||
| 229.1 | M1(2; -5), M2(3; 2); | |
| 229.2 | P(-3, 1), Q(7; 8); | |
| 229.3 | A(5; -3), B(-1; 6).

| |
Составить уравнения прямых, проходящих через вершины треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно противоположным сторонам.
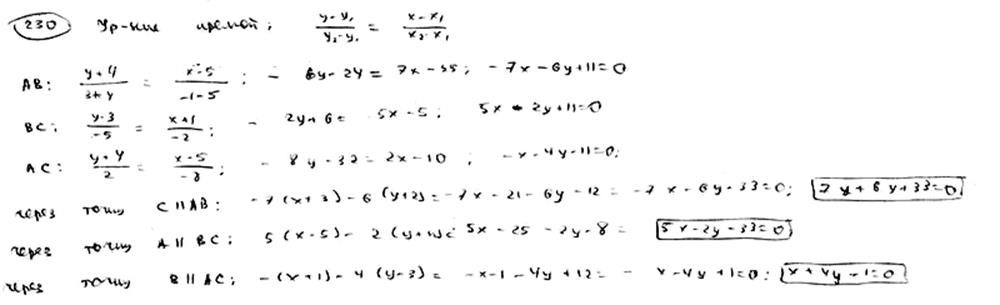
| ||
Даны середины сторон треугольника M1(2; 1), M2(5; 3), M3(3; -4). Составить уравнение его сторон.

| ||
Даны две точки P(2; 3), Q(-1; 0). Составить уравнение прямой, проходящей через точку Q перпендикулярно к отрезку  . .

| ||
Составить уравнение прямой, если точка P(2; 3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.
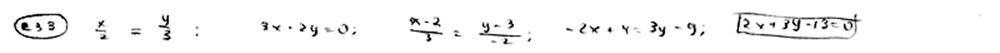
| ||
Даны вершины треугольника M1(2; 1), M2(-1; -1), M3(3; 2). Составить уравнения его высот.
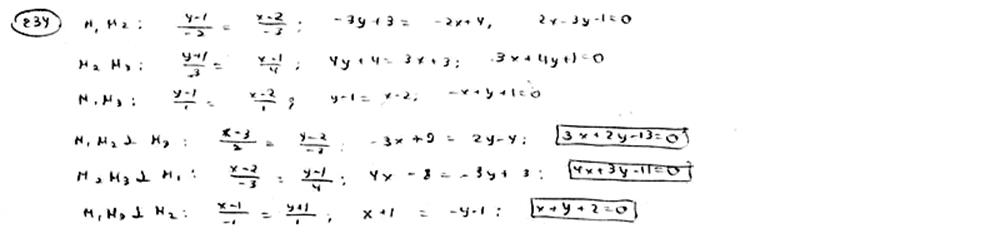
| ||
Стороны треугольника даны уравнениями  , ,  , ,  . Определить точку пересечения его высот. . Определить точку пересечения его высот.
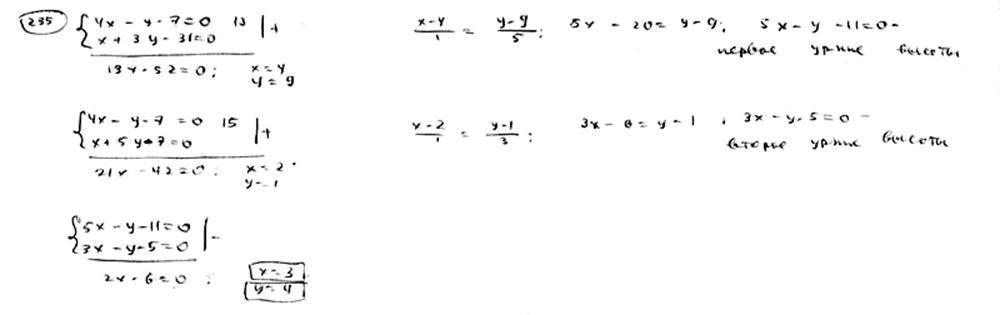
| ||
Даны вершины треугольника A(1; -1), B(-2; 1), C(3; 5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану, проведенную из вершины В.

| ||
Даны вершины треугольника A(2; -2), B(3; -5), C(5; 7). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине А.

| ||
Составить уравнения сторон и медиан треугольника с вершинами A(3; 2), B(5; -2), C(1; 0).

| ||
Через точки M1(-1; 2), M2(2; 3) проведена прямая. Определить точки пересечения этой прямой с осями координат.

| ||
Доказать, что условие, при котором три точки M1(x1, y1), M2(x2, y2), M3(x3, y3) лежат на одной прямой, может быть записано в следующем виде:


| ||
Доказать, что уравнение прямой, проходящей через две данные точки M1(x1, y1), M2(x2, y2), может быть записано в следующем виде:


| ||
Даны последовательные вершины выпуклого четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6). Определить точку пересечения его диагоналей.

| ||
Даны две смежные вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3; 0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма.

| ||
Даны уравнения двух сторон прямоугольника  , ,  и уравнение его диагонали и уравнение его диагонали  . Составить уравнения остальных сторон и второй диагонали этого прямоугольника. . Составить уравнения остальных сторон и второй диагонали этого прямоугольника.

| ||
Даны вершины треугольника A(1; -2), B(5; 4), C(-2; 0). Составить уравнения биссектрис его внутреннего и внешнего углов при вершине А.

| ||
Составить уравнение прямой, проходящей через точку P(3; 5) на одинаковых расстояниях от точек A(-7; 3) и B(11; -15).

| ||
Найти проекцию точки P(-8; 12) на прямую, проходящую через точки A(2; -3), B(-5; 1).

| ||
Найти точку M1, симметричную точке М2(8; -9) относительно прямой, проходящей через точки А(3; -4), B(-1; -2).

| ||
На оси абсцисс найти такую точку P, чтобы сумма ее расстояний до точек M(1; 2), N(3; 4) была наименьшей.

| ||
На оси ординат найти такую точку P, чтобы сумма ее расстояний до точек M(-3; 2), N(2; 5) была наибольшей.

| ||
На прямой  найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей. найти такую точку Р, сумма расстояний которой до точек A(-7; 1), B(-5; 5) была бы наименьшей.

| ||
На прямой  найти такую точку Р, разность расстояний которой до точек A(4; 1), B(0; 4) была бы наибольшей. найти такую точку Р, разность расстояний которой до точек A(4; 1), B(0; 4) была бы наибольшей.

| ||
Определить угол  между двумя прямыми: между двумя прямыми:
| ||
| 253.1 | 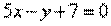 , ,  ; ;
| |
| 253.2 |  , ,  ; ;
| |
| 253.3 |  , ,  ; ;
| |
| 253.4 |  , ,  . .

| |
Дана прямая  . Составить уравнение прямой, проходящей через точку M0(2; 1) под углом 450 к данной прямой. . Составить уравнение прямой, проходящей через точку M0(2; 1) под углом 450 к данной прямой.

| ||
Точка А(-4; 5) является вершиной квадрата, диагональ которого лежит на прямой 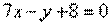 . Составить уравнения сторон и второй диагонали этого квадрата. . Составить уравнения сторон и второй диагонали этого квадрата.

| ||
Даны две противоположные вершины квадрата A(-1; 3), C(6; 2). Составить уравнения его сторон.

| ||
Точка E(1; -1) является центром квадрата, одна из сторон которого лежит на прямой  . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата. . Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.

| ||
Из точки M0(-2; 3) под углом 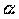 к оси Ox направлен луч света. Известно, что к оси Ox направлен луч света. Известно, что  . Дойдя до оси Ox, луч от нее отразился. Составить уравнения прямых, на которых лежат падающий и отраженный лучи. . Дойдя до оси Ox, луч от нее отразился. Составить уравнения прямых, на которых лежат падающий и отраженный лучи.

| ||
Луч света направлен по прямой  , луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч. , луч от нее отразился. Составить уравнение прямой, на которой лежит отраженный луч.

| ||
Даны уравнения сторон треугольника  , ,  , ,  . Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника. . Доказать, что этот треугольник равнобедренный. Решить задачу при помощи сравнения углов треугольника.

| ||
Доказатть, что уравнение прямой, проходящей через точку M1(x1; y1) параллельно прямой 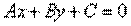 , может быть записано в виде , может быть записано в виде  . .

| ||
| Составить уравнение прямой, проходящей через точку М1(2: -3) параллельно прямой: | ||
| 262.1 |  ; ;
| |
| 262.2 | 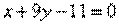 ; ;
| |
| 262.3 | 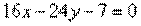 ; ;
| |
| 262.4 | 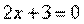 ; ;
| |
| 262.5 |  . .

| |
Доказать, что условие перпендикулярности прямых  ; ;  может быть записано в следующем виде: может быть записано в следующем виде:  . .

| ||
| Установить, какие из следующих пар прямых перпендикулярны. Решить задачу, не вычисляя угловых коэффициентов данных прямых. | ||
| 264.1 |  , ,  ; ;
| |
| 264.2 |  , ,  ; ;
| |
| 264.3 |  , ,  ; ;
| |
| 264.4 |  , ,  ; ;
| |
| 264.5 |  , ,  ; ;
| |
| 264.6 |  , ,  . .

| |
Доказать, что формула для определения угла  между прямыми между прямыми  , ,  может быть записана в следующей форме: может быть записана в следующей форме:


| ||
Определить угол  , образованный двумя прямыми. Решить задачу, не вычисляя угловых коэффициентов данных прямых. , образованный двумя прямыми. Решить задачу, не вычисляя угловых коэффициентов данных прямых.
| ||
| 266.1 |  , ,  ; ;
| |
| 266.2 |  , ,  ; ;
| |
| 266.3 |  , ,  . .

| |
Даны две вершины треугольника M1(-10; 2), M2(6; 4); его высоты пересекаются в точке N(5; 2). Определить координаты третьей вершины M3.

| ||
Даны две вершины A(3; -1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения его высот. Составить уравнения сторон этого треугольника.
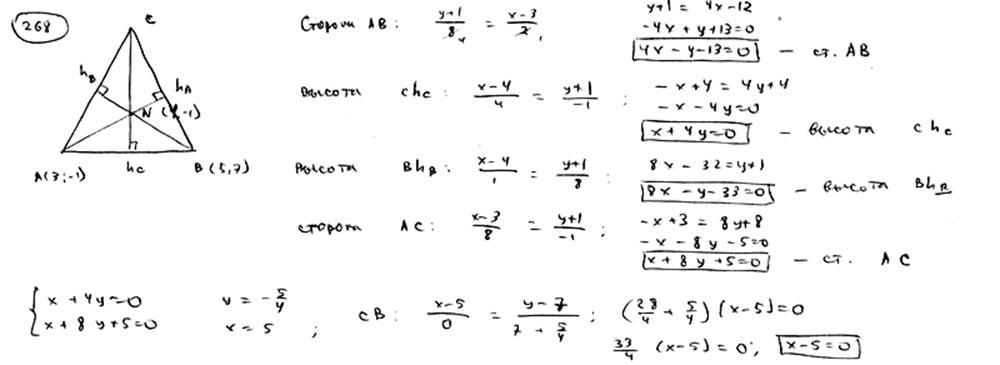
| ||
В треугольнике АВС даны: уравнение стороны АВ:  , уравнения высот АМ: , уравнения высот АМ:  и BN: и BN:  . Составить уравнения двух других сторон и третьей высоты этого треугольника. . Составить уравнения двух других сторон и третьей высоты этого треугольника.

| ||
Составить уравнения сторон треугольника АВС, если даны одна из его вершина А(1; 3) и уравнения двух медиан 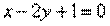 , ,  . .

| ||
Составить уравнения сторон треугольника, сли даны одна из его вершин B(-4; -5) и уравнения двух высот  , ,  . .

| ||
Составить уравнения сторон треугольника, зная одну из его вершин A(4; -1) и уравнения двух биссектрис  , ,  . .

| ||
Составить уравнения сторон треугольника, зная одну из его вершин B(2; 6), а также уравнения высоты  и биссектрисы и биссектрисы  , проведенных из одной вершины. , проведенных из одной вершины.

| ||
Составить уравнения сторон треугольника, зная одну его вершину B(2; -1), а также уравнения высоты 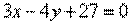 и биссектрисы и биссектрисы  , проведенных из различных вершин. , проведенных из различных вершин.

| ||
Составить уравнения сторон треугольника, зная одну его вершину C(4; -1), а также уравнения высоты  и медианы и медианы 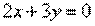 , проведенной из одной вершины. , проведенной из одной вершины.

| ||
Составить уравнения сторон треугольника, зная одну его вершину B(2; -7), а также уравнения высоты  и медианы и медианы  , проведенных из различных вершин. , проведенных из различных вершин.

| ||
Составить уравнения сторон треугольника, зная одну его вершину C(4; 3), а также уравнения биссектрисы  и медианы и медианы  , проведенных из одной вершины. , проведенных из одной вершины.

| ||
Составить уравнения сторон треугольника, зная одну его вершину A(3; -1), а также уравнения биссектрисы  и медианы и медианы  , проведенных из различных вершин. , проведенных из различных вершин.

| ||
Составить уравнение прямой, которая проходит черезначало координат и вместе с прямыми  , ,  образует треугольник с площадью, равной 1,5. образует треугольник с площадью, равной 1,5.

| ||
Среди прямых, проходящих через точку P(3; 0), найти такую, отрезок которой, заключенный между прямыми  , ,  , делится в точке Р пополам. , делится в точке Р пополам.

| ||
Через точку Р(-3; -1) проведены всевозможные прямые. Доказать, что отрезок каждой из них, заключенный между прямыми  , ,  , делится в точке Р пополам. , делится в точке Р пополам.

| ||
Через точку Р(0; 1) проведены всевозможные прямые. Доказать, что среди них нет прямой, отрезок которой, заключенный между прямыми  , ,  , делился бы в точке Р пополам. , делился бы в точке Р пополам.

| ||
Составить уравнение прямой, проходящей через начало координат, зная, что длина ее отрезка, заключенного между прямыми  , ,  , равна , равна  . .

| ||
Составить уравнение прямой, проходящей через точку С(-5; 4), зная, что длина ее отрезка, заключенного между прямыми  , ,  , равна 5. , равна 5.

|
Глава 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трех прямых. Уравнение прямой "в отрезках"
|
Просмотров 2370 |
|
|
