
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

МАТЕМАТИЧНИЙ ОПИС НЕЛІНІЙНОСТЕЙ
|
|
ЗАВДАННЯ ДЛЯ РОЗРАХУНКУ
1. Описати аналітично нелінійність (рисунок 2.1). Навести приклади та принцип дії реальних систем, робота яких описується нелінійністю такого роду.
2. Виконати операції над нечіткими множинами (таблиця 2.1) з заданим видом функцій приналежності (рисунок 2.2) та скласти математичний опис функції приналежності результуючої множини.

Рисунок 2.1 – Вихідна нелінійність
Таблиця 2.1 - Варіант завдання
| № варіанту | № нечіт. множ. | Операції над множинами |
| A7 | 
|

Рисунок 2.2 – Функція приналежності нечітких множин А7
РОЗРАХУНОК ЗАВДАННЯ № 2.1
Нелінійність, яка приведена на рисунку 2.1, є типовою нелінійністю – «люфт».
Майже будь-яке механічне з’єднання в тій чи іншій мірі має люфт. Люфт механічної передачі характеризується величиною повороту одного з елементів передачі, що не викликає поворот іншого. Найбільш часто в СУ зустрічається люфт в зубчатих зачепленнях, редукторах, плаваючих муфтах. В зубчатих передачах люфт обумовлений зазором між сусідніми зубцями шестерень, які зчіплюються, завдяки чому ведуче колесо може повертатися на деякий кут, не вступаючи у силовий контакт з відомим колесом.
При зростанні (убуванні) координат x в інтервалі [-x2; x2] одночасно зростає (убуває) координата y, а нелінійність описується прямими лініями 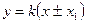 , де
, де  . Знак «+» відповідає убуванню, «-» - зростанню. Особливістю нелінійності є наявність переходів з однієї характеристики на іншу. Під час переходу координата x починає змінюватися в зворотному напрямку, а координата у залишається постійною не залежно від значення величини х і рівною
. Знак «+» відповідає убуванню, «-» - зростанню. Особливістю нелінійності є наявність переходів з однієї характеристики на іншу. Під час переходу координата x починає змінюватися в зворотному напрямку, а координата у залишається постійною не залежно від значення величини х і рівною  , де xп - значення величини x, при якому починається перехід (послідовності знаків «-», «+» відповідає перехід з лінії
, де xп - значення величини x, при якому починається перехід (послідовності знаків «-», «+» відповідає перехід з лінії  до
до  та «-», «+» - навпаки). Аналітичний вираз для розглянутої нелінійності:
та «-», «+» - навпаки). Аналітичний вираз для розглянутої нелінійності:

де  .
.
РОЗРАХУНОК ЗАВДАННЯ № 2.2
Виконаємо операції  над нечіткими множинами A, В, С з функціями приналежності
над нечіткими множинами A, В, С з функціями приналежності  ,
,  ,
,  відповідно (рисунок 2.2).
відповідно (рисунок 2.2).
Результат перетину нечітких множин  , В та С, об’єднаний з множиною А – нечітка множина D, яка наведена на рисунку 2.3.
, В та С, об’єднаний з множиною А – нечітка множина D, яка наведена на рисунку 2.3.

Рисунок 2.3 - Результат операцій  між нечіткими множинами
між нечіткими множинами
З рисунку 2.3 видно, що функція приналежності  , що описує множину D являє собою функцію, умовно розбиту на шість ділянок з різним математичним описом:
, що описує множину D являє собою функцію, умовно розбиту на шість ділянок з різним математичним описом:
- при  й
й  функція приналежності приймає постійне значення
функція приналежності приймає постійне значення  ;
;
- при  описується лініями
описується лініями  ;
;
- при  ,
,  й
й  описується прямими лініями.
описується прямими лініями.
Рівняння прямої на інтервалі  побудуємо за двома точками
побудуємо за двома точками  і
і  :
:  ;
;
 .
.
Рівняння прямої на інтервалі  :
: 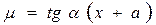 .
.
Математичний опис функції приналежності  :
:

Завдання № 3
ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ
ЗАВДАННЯ ДЛЯ РОЗРАХУНКУ
1. Знайти наближення функції  на інтервалі
на інтервалі  з використанням лінійного P1(x), квадратичного P2(x) та кубічного P3(x) поліномів Лагранжа. Для значень x, що розбивають інтервал
з використанням лінійного P1(x), квадратичного P2(x) та кубічного P3(x) поліномів Лагранжа. Для значень x, що розбивають інтервал  з кроком h, розрахувати значення функції
з кроком h, розрахувати значення функції  , поліномів Лагранжа P1(x), P2(x), P3(x) та представити рішення в табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Визначити помилки наближень. Порівняти результати наближення функції з точним розв’язком
, поліномів Лагранжа P1(x), P2(x), P3(x) та представити рішення в табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Визначити помилки наближень. Порівняти результати наближення функції з точним розв’язком  та проаналізувати точність поліномів Лагранжа між собою. Необхідні дані взяти з таблиці 3.1.
та проаналізувати точність поліномів Лагранжа між собою. Необхідні дані взяти з таблиці 3.1.
2. Побудувати таблицю різницевих відношень для функції  за точками xk,
за точками xk,  та знайти поліноми Ньютона P1(x), P2(x), P3(x), P4(x). Для значень x, що розбивають інтервал [a; b] з кроком h, розрахувати значення функції
та знайти поліноми Ньютона P1(x), P2(x), P3(x), P4(x). Для значень x, що розбивають інтервал [a; b] з кроком h, розрахувати значення функції  , поліномів Ньютона P1(x), P2(x), P3(x), P4(x) та представити рішення в табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Порівняти результати наближення функції з точним розв’язком
, поліномів Ньютона P1(x), P2(x), P3(x), P4(x) та представити рішення в табличному й графічному вигляді з використанням пакетів Mathcad та Matlab. Порівняти результати наближення функції з точним розв’язком  та проаналізувати точність поліномів Ньютона між собою. Необхідні дані взяти з таблиці 3.1.
та проаналізувати точність поліномів Ньютона між собою. Необхідні дані взяти з таблиці 3.1.
3. Знайти наближення Паде RN,M(x) для функції  . Представити рішення у графічному вигляді з використанням пакетів Mathcad чи Matlab. Визначити помилку наближення. Необхідні дані взяти з таблиці 3.2.
. Представити рішення у графічному вигляді з використанням пакетів Mathcad чи Matlab. Визначити помилку наближення. Необхідні дані взяти з таблиці 3.2.
Таблиця 3.1 - Варіант завдання для побудови наближуючих функцій
| № | Функція | Інтерполяційні поліноми | |||
| Лагранжа | Ньютона | ||||
| P1(x) | P2(x) | P3(x) | Pk(x), k=1..4 | ||
 a=0; b=3; h=0.1
a=0; b=3; h=0.1
| 
| 
| 
| 
|
Таблиця 3.2 - Варіант завдання для побудови наближення Паде
| № | Функція f(x) | Наближення Паде |

| R3, 2(x) |
РОЗРАХУНОК ЗАВДАННЯ № 3.1
Побудуємо лінійний поліном P1(x) за точками  і
і  , використовуючи
, використовуючи
 з абсцисами
з абсцисами  і
і  , та ординатами
, та ординатами 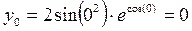 і
і  :
:

Побудуємо інші поліноми Лагранжа: квадратичний P2(x) за трьома вузлами  ,
,  і
і  ; кубічний поліном P3(x) за чотирма –
; кубічний поліном P3(x) за чотирма – 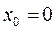 ,
,  ,
,  і
і  .
.
Виконаємо підстановку  ,
,  ,
,  і
і 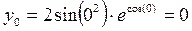 ,
,  ,
,  у формулу
у формулу  , отримаємо:
, отримаємо:

Підставивши 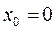 ,
,  ,
,  і
і  і
і 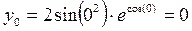 ,
,  ,
,  ,
,  у формулу
у формулу  , отримаємо:
, отримаємо:

 .
.
Значення помилок наближень Лагранжа E1(x), E2(x), E3(x) для поліномів P1(x), P2(x), P3(x) відповідно наведені в таблиці 3.3.
Таблиця 3.3 - Порівняння значень функції f(x) з лінійним, квадратичним і кубічним наближеннями Лагранжа P1(x), P2(x), P3(x)
| xk | 
| E1(xk)= f(xk)-P1(xk) | E2(xk)= f(xk)-P2(xk) | E3(xk)= f(xk)-P3(xk) |
| 0.0 | 0.0000000 | 0.0000000 | 0.0000000 | 0.0000000 |
| 0.1 | 0.0540938 | 0.0438848 | -0.1516448 | -0.0027889 |
| 0.2 | 0.2131139 | 0.1926959 | -0.1848785 | -0.0000855 |
| 0.3 | 0.4672867 | 0.4366597 | -0.1094747 | -0.0000476 |
| Продовження таблиці 3.3 | ||||
| 0.4 | 0.8004001 | 0.7595641 | 0.0583545 | -0.0000000 |
| 0.5 | 1.1900519 | 1.1390069 | 0.2962069 | -0.0000361 |
| 0.6 | 1.6082353 | 1.5469813 | 0.5760757 | -0.0000890 |
| 0.7 | 2.0224256 | 1.9509626 | 0.8654362 | -0.0000351 |
| 0.8 | 2.3972999 | 2.3156279 | 1.1289655 | -0.0001267 |
| 0.9 | 2.6971343 | 2.6052533 | 1.3309397 | -0.0000438 |
| 1.0 | 2.8888131 | 2.7867231 | 1.4382431 | 0.0000000 |
| 1.1 | 2.9452484 | 2.8329494 | 1.4237878 | 0.0000724 |
| 1.2 | 2.8488819 | 2.7263739 | 1.2700155 | 0.0001743 |
| 1.3 | 2.5948387 | 2.4621217 | 0.9720513 | 0.0000941 |
| 1.4 | 2.1932433 | 2.0503173 | 0.5400197 | 0.0001052 |
| 1.5 | 1.6702106 | 1.5170756 | 0.0000000 | 0.0001376 |
| 1.6 | 1.0670929 | 0.9037489 | -0.6065487 | 0.0000789 |
| 1.7 | 0.4377035 | 0.2641505 | -1.2259199 | 0.0000888 |
| 1.8 | -0.156561 | -0.340323 | -1.7966814 | 0.0002412 |
| 1.9 | -0.6535095 | -0.8474805 | -2.2566421 | 0.0000933 |
| 2.0 | -0.9983487 | -1.2025287 | -2.5510087 | 0.0000000 |
| 2.1 | -1.1524237 | -1.3668127 | -2.6411263 | 0.0000356 |
| 2.2 | -1.1012893 | -1.3258873 | -2.5125497 | 0.0000772 |
| 2.3 | -0.8605865 | -1.0953935 | -2.1809199 | 0.0001284 |
| 2.4 | -0.4780164 | -0.7230324 | -1.693938 | 0.0000845 |
| 2.5 | -0.0297827 | -0.2850077 | -1.1278077 | 0.0000937 |
| 2.6 | 0.3896321 | 0.1241981 | -0.5770115 | 0.0000625 |
| 2.7 | 0.6844185 | 0.4087755 | -0.1373589 | 0.0000261 |
| 2.8 | 0.7794452 | 0.4935932 | 0.1160188 | 0.0000883 |
| 2.9 | 0.6433418 | 0.3472808 | 0.1517512 | 0.0000752 |
| 3.0 | 0.3062695 | 0.0000000 | 0.0000000 | 0.0000000 |
У таблиці 3.4 наведені оцінки середньоквадратичних відхилень помилок наближень поліномами Лагранжа P1(x), P2(x), P3(x), що розраховуються за формулою: 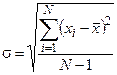 ,
,
де  - значення вибірки з N елементів;
- значення вибірки з N елементів;
 - математичне очікування чи середнє арифметичне вибірки.
- математичне очікування чи середнє арифметичне вибірки.
Таблиця 3.4 - Оцінки середньоквадратичних відхилень помилок наближень поліномами Лагранжа.
| Поліном | P1(x), k=1 | P2(x), k=2 | P3(x), k=3 |

| 0.034368 | 0.003796 | 0.000367 |
Наближення поліномом P3(x) до  має найкращу точність, оскільки має найменше значення середньоквадратичного відхилення помилки. З таблиці 3.4 видно, що зі збільшенням ступеня інтерполяційного поліному підвищується точність наближення до функції
має найкращу точність, оскільки має найменше значення середньоквадратичного відхилення помилки. З таблиці 3.4 видно, що зі збільшенням ступеня інтерполяційного поліному підвищується точність наближення до функції  .
.
Графіки наближення функції  лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа наведені на рисунку 3.1, де чорними точками позначені вузли інтерполяції.
лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа наведені на рисунку 3.1, де чорними точками позначені вузли інтерполяції.

Рисунок 3.1 - Графіки наближення функції  лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа на інтервалі [0; 3]
лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа на інтервалі [0; 3]
Графіки помилок наближень  ,
,  ,
,  відповідно лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа зображені на рисунку 3.2, де чорними точками позначені вузли інтерполяції.
відповідно лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа зображені на рисунку 3.2, де чорними точками позначені вузли інтерполяції.

Рисунок 3.2 - Графіки помилок наближень функції  лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа на інтервалі [0; 3]
лінійним P1(x), квадратичним P2(x) і кубічним P3(x) поліномами Лагранжа на інтервалі [0; 3]
РОЗРАХУНОК ЗАВДАННЯ № 3.2
Наступна модель обчислень показує, як знайти коефіцієнт a2 через різницеві відношення:

Значення різницевих відношень наведені в таблиці 3.5.
Таблиця 3.5 - Таблиця різницевих відношень для функції 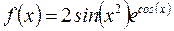

| 
| 
| 
| 
| 
|

| 0. 0000000 | ||||

| 2. 8881 | 2. 88881 | |||

| -0. 99835 | -3. 88716 | -3. 387985 | ||

| 0. 30627 | 1. 30462 | 2. 59589 | 1. 994625 | |

| -0. 299506 | -0. 60583 | -0. 955225 | -1. 183705 | -0. 7945825 |
Використаємо таблицю 3.5, щоб знайти коефіцієнти ak і чотири інтерполяційні поліноми Ньютона Pk(x) для k=1, 2, 3, 4.
Запишемо поліноми Ньютона з використанням формули  за вузлами
за вузлами  і елементами
і елементами  (коефіцієнтам поліномів Ньютона), які знаходяться на діагоналі таблиці 3.5:
(коефіцієнтам поліномів Ньютона), які знаходяться на діагоналі таблиці 3.5:

Значення помилок наближень E1(x), E2(x), E3(x), E4(x) для поліномів Ньютона P1(x), P2(x), P3(x), P4(x) відповідно наведені в таблиці 3.6.
Таблиця 3.6 - Порівняння f(x) з наближеннями Ньютона P1(x), P2(x), P3(x), P4(x)
| xk | f(xk) | E1(xk) | E2(xk) | E3(xk) | E4(xk) |
| 0.0 | 0.0000000 | 0.000000 | 0.0000000 | 0.000000 | 0.000000 |
| 0.1 | 0.0540938 | -0.2347872 | -0.5397058 | -0.068752 | -1.2748202 |
| 0.2 | 0.2131139 | -0.3646481 | -0.9067257 | -0.296410 | -2.1219291 |
| 0.3 | 0.4672867 | -0.3993563 | -1.1108332 | -0.879301 | -2.5888124 |
| 0.4 | 0.8004001 | -0.3551239 | -1.1682403 | -1.274638 | -2.7274875 |
| 0.5 | 1.1900519 | -0.2543531 | -1.1013493 | -1.849229 | -2.5942548 |
| 0.6 | 1.6082353 | -0.1250507 | -0.9381671 | -1.380627 | -2.2491125 |
| 0.7 | 2.0224256 | 0.0002586 | -0.7112183 | -0.764390 | -1.7546692 |
| 0.8 | 2.3972999 | 0.0862519 | -0.4558257 | -0.196388 | -1.1744254 |
| 0.9 | 2.6971343 | 0.0972053 | -0.2077134 | -0.038764 | -0.5703749 |
| 1.0 | 2.8888131 | 0.0000000 | 0.0000000 | 0.000000 | 0.000000 |
| 1.1 | 2.9452484 | -0.2324426 | 0.1402358 | 0.3377036 | 0.4871646 |
| 1.2 | 2.8488819 | -0.6176901 | 0.1954263 | 0.5783943 | 0.853002 |
| 1.3 | 2.5948387 | -1.1606143 | 0.1606999 | 0.7052325 | 1.0739982 |
| 1.4 | 2.1932433 | -1.8510907 | 0.0461809 | 0.7163749 | 1.1435425 |
| 1.5 | 1.6702106 | -2.6630044 | -0.1220157 | 0.6259687 | 1.0729213 |
| 1.6 | 1.0670929 | -3.5550031 | -0.3025375 | 0.4633985 | 0.8905661 |
| 1.7 | 0.4377035 | -4.4732735 | -0.4415713 | 0.2705098 | 0.6392756 |
| 1.8 | -0.156561 | -5.356419 | -0.4777206 | 0.0967314 | 0.3713391 |
| 1.9 | -0.6535095 | -6.1422485 | -0.3487942 | 0.0007643 | 0.1417477 |
| 2.0 | -0.9983487 | -6.7759687 | 0.0000000 | 0.0000000 | 0.0000000 |
| 2.1 | -1.1524237 | -7.2189247 | 0.6073206 | 0.1465623 | -0.0186314 |
| 2.2 | -1.1012893 | -7.4566713 | 1.4876091 | 0.4344471 | 0.0988155 |
| 2.3 | -0.8605865 | -7.5048495 | 2.6252256 | 0.836047 | 0.3371287 |
| 2.4 | -0.4780164 | -7.4111604 | 3.9724692 | 1.2916932 | 0.6509419 |
| 2.5 | -0.0297827 | -7.2518077 | 5.4531361 | 1.7132142 | 0.9682931 |
| 2.6 | 0.3896321 | -7.1212739 | 6.9727437 | 1.9941597 | 1.2008485 |
| 2.7 | 0.6844185 | -7.1153685 | 8.4354826 | 2.0267525 | 1.2608544 |
| 2.8 | 0.7794452 | -7.3092228 | 9.7662216 | 1.7238936 | 1.0831423 |
| 2.9 | 0.6433418 | -7.7342072 | 10.9335901 | 1.0422448 | 0.6482113 |
| 3.0 | 0.3062695 | -8.3601605 | 11.9677495 | 0.0000000 | 0.0000000 |
У таблиці 3.7 наведені оцінки середньоквадратичних відхилень помилок наближень поліномами Ньютона P1(x), P2(x), P3(x), P4(x).
Таблиця 3.7 - Оцінки середньоквадратичних відхилень помилок наближень поліномами Ньютона
| Поліном | P1(x), k=1 | P2(x), k=2 | P3(x), k=3 | P4(x), k=4 |

| 1.253984 | 0.729846 | 0.081063 | 0.285676 |
Аналіз таблиці 3.7 показує, що поліном Ньютона з найвищим ступенем P4(x) не є найкращим наближенням функції 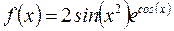 . Для наближення
. Для наближення 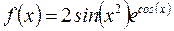 на відрізку [0; 3] краще використовувати поліном P3(x), оскільки він має найменше значення оцінки середньоквадратичного відхилення помилки наближення.
на відрізку [0; 3] краще використовувати поліном P3(x), оскільки він має найменше значення оцінки середньоквадратичного відхилення помилки наближення.
Графіки наближення функції 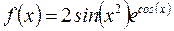 поліномами Ньютона різного ступеня P1(x), P2(x), P3(x), P4(x)наведені на рисунку 3.3, де чорними точками позначені вузли інтерполяції.
поліномами Ньютона різного ступеня P1(x), P2(x), P3(x), P4(x)наведені на рисунку 3.3, де чорними точками позначені вузли інтерполяції.
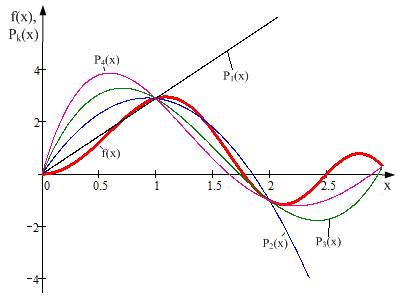
Рисунок 3.3 - Графіки наближення функції 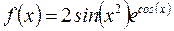 поліномами Ньютона різного ступеня на інтервалі [0; 3]
поліномами Ньютона різного ступеня на інтервалі [0; 3]
Графіки помилок наближень  ,
,  ,
,  ,
,  відповідними поліномами Ньютона P1(x), P2(x), P3(x), P4(x) зображені на рисунку 3.4, де чорними точками позначені вузли інтерполяції.
відповідними поліномами Ньютона P1(x), P2(x), P3(x), P4(x) зображені на рисунку 3.4, де чорними точками позначені вузли інтерполяції.

Рисунок 3.4 - Графіки помилок наближень функції 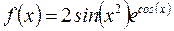 поліномами Ньютона різного ступеня на інтервалі [0; 3]
поліномами Ньютона різного ступеня на інтервалі [0; 3]
З таблиць 3.4 і 3.7 видно, що поліноми Лагранжа в порівнянні з поліномами Ньютона того ж ступеня дають меншу помилку наближення до функції 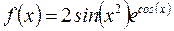 на інтервалі [0; 3]. У зв’язку з цим, при вирішенні різних задач для інтерполяції
на інтервалі [0; 3]. У зв’язку з цим, при вирішенні різних задач для інтерполяції 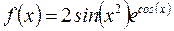 функції на інтервалі [0; 3] краще використовувати поліноми Лагранжа.
функції на інтервалі [0; 3] краще використовувати поліноми Лагранжа.
РОЗРАХУНОК ЗАВДАННЯ № 3.3
Виконаємо розклад функції  у ряд Маклорена:
у ряд Маклорена:

З урахуванням розкладання Маклорена рівняння 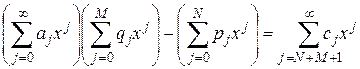 приймає вигляд:
приймає вигляд:

Виконавши перетворення та дорівнявши коефіцієнти при перших шести ступенях x у лівій і правій частинах, отримаємо дві системи з дев’яти лінійних рівнянь:
 ;
;  .
.
Розв’язок спочатку другої, а потім першої з отриманих систем лінійних рівнянь дозволяє знайти значення невідомих коефіцієнтів наближення Паде: 


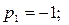
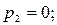
 .
.
Тоді раціональне наближення Паде R3,2(x) для функції  :
:
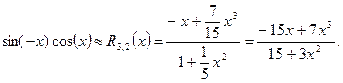
На рисунку 3.5 представлені графіки функції  і її наближення за допомогою рядів Паде R3,2(x). Графік помилки ЕR(x) наближення Паде R3,2(x) зображений на рисунку 3.6.
і її наближення за допомогою рядів Паде R3,2(x). Графік помилки ЕR(x) наближення Паде R3,2(x) зображений на рисунку 3.6.

Рисунок 3.5 - Наближення Паде R3,2(x) для функції 

Рисунок 3.6 - Графік помилки наближення Паде R3,2(x) для функції 
Завдання № 4
|
Просмотров 655 |
|
|
