Количественные и качественные характеристики информации

Информационные меры, как правило, рассматриваются в трех аспектах: структурном, статис-тическом и семантическом.

В структурном аспекте рассматривается строение массивов информации и их измерение простым подсчетом информационных элементов или комбинаторным методом. Структурный подход применяется для оценки возможностей информационных систем вне зависимости от условий их применения.

При статистическом подходе используется понятие энтропии как меры неопределенности, учитывающей вероятность появления и информативность того или иного сообщения. Статистический подход учитывает конкретные условия применения информационных систем.

Семантический подход позволяет выделить полезность или ценность информационного сообщения.

Структурная мера информации

Информация всегда представляется в виде сообщения. Элементарная единица сообщений – символ. Символы, собранные в группы, – слова. Сообщение, оформленное в виде слов или отдельных символов, всегда передается в материально-энергетической форме (электрический, световой, звуковой сигналы).

Различают информацию непрерывную и дискретную (рис. 2.4).

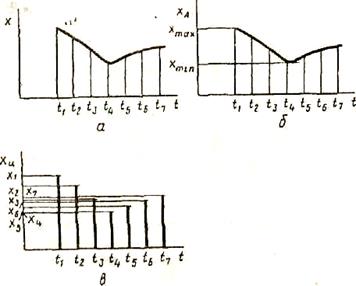
Рис. 2.4. Способы представления информации

Функция x(t), изображенная на рис. 2.4 а, может быть представлена в непрерывном (рис. 2.4 б) и дискретном (рис. 2.4 в) видах. В непрерывном виде эта функция может принимать любые вещественные значения в данном диапазоне изменения аргумента t, т.е. множество значений непрерывной функции бесконечно. В дискретном виде функция x(t) может принимать вещест-венные значения только при определенных значениях аргумента. Какой бы малый интервал дискретности (т.е. расстояние между соседними значениями аргумента) ни выбирался, множество значений дискретной функции для заданного диапазона изменений аргумента (если он не бесконечный) будет конечно (ограничено).

При использовании структурных мер информации учитывается только дискретное строение сообщения, количество содержащихся в нем информационных элементов, связей между ними. При структурном подходе различаются геометрическая, комбинаторная и аддитивная меры информации.

Геометрическая мера предполагает измерение параметра геометрической модели информа-ционного сообщения (длины, площади, объема) в дискретных единицах. Например, геометричес-кой моделью информации может быть линия единичной длины (рис 2.5 а – одноразрядное слово, принимающее значение 0 или 1), квадрат (рис. 2.5 б – двухразрядное слово) или куб (рис 2.5 в – трехразрядное слово). Максимально возможное количество информации в заданных структурах определяет информационную емкость модели (системы), которая определяется как сумма дискретных значений по всем измерениям (координатам).

Рис. 2.5.Геометрическая модель информации

В комбинаторной мере количество информации определяется как число комбинаций элементов (символов). Возможное количество информации совпадает с числом возможных сочетаний, перестановок и размещений элементов. Комбинирование символов в словах, состоящих только из 0 и 1, меняет значения слов. Рассмотрим две пары слов 100110 и 001101, 011101 и 111010. В них проведена перестановка крайних разрядов (изменено местоположение знакового разряда в числе – разряд перенесен слева направо).

Аддитивная мера (мера Хартли),в соответствии с которой количество информации измеряется в двоичных единицах (битах), наиболее распространена. Вводятся понятия глубины и длины числа.

Глубина числа (q)–количество символов (элементов), принятых для представления инфор-мации. В каждый момент времени реализуется только один какой-либо символ. Глубина числа соответствует основанию системы счисления.

Длина числа (n)–количество позиций, необходимых и достаточных для представления чисел заданной величины. Длина числа соответствует разрядности системы счисления.

При заданных глубине и длине числа количество чисел, которое можно представить, будет
N = qⁿ. Величина N неудобна для оценки информационной емкости. Хартли ввел аддитивную двоичную логарифмическую меру, позволяющую вычислять количество информации в двоичных единицах – битах:

I = log₂N = nlog₂q.

При n = 1, q = 2

I = log₂2=1 бит.

Это и есть единица информации по Хартли.

Следовательно, 1 бит информации соответствует одному элементарному событию, которое может произойти или не произойти. Такая мера количества информации удобна тем, что она обеспечивает возможность оперировать мерой как числом. Количество информации при этом эквивалентно количеству двоичных символов 0 или 1. При наличии нескольких источников информации общее количество информации

I(q₁, q₂, …, q_k) = I (q₁) + I (q₂) + …. + I (q_k),

где I(q_k) – количество информации от источника k. Логарифмическая мера информации позволяет измерять количество информации и используется на практике.

Статистическая мера информации

В статистической теории информации вводится мера количества информации, в соответствии с которой рассматривается не само событие, а информация о нем. Этот вопрос проработан
К. Шенноном в работе "Избранные труды по теории информации". Если появляется сообщение
о часто встречающемся событии, вероятность появления которого близка к единице, то такое сообщение для получателя малоинформативно. Столь же малоинформативны сообщения о собы-тиях, вероятность появления которых близка к нулю.

События можно рассматривать как возможные исходы некоторого опыта, причем все исходы этого опыта составляют полную группу событий. К. Шеннон ввел понятие неопределенности ситуации, возникающей в процессе опыта, назвав ее энтропией.

Энтропияполной группы событий есть количественная мера ее неопределенности и, следова-тельно, информативности, количественно выражаемая как средняя функция множества вероят-ностей каждого из возможных исходов опыта. Количество информации, получаемое в результате проведения опыта, равно неопределенности, снятой во время этого опыта.

Вероятностный подход проще всего объяснить на примере, связанном с бросанием правиль-ной игральной кости, имеющей N граней (наиболее распространенным является случай шестигранной кости: N = 6). Результатом данного опыта может быть выпадение грани с одним из следующих знаков: 1, 2, ... , N.

Введем в рассмотрение численную величину, измеряющую неопределенность – энтропию (обозначим ее Н). Величины N и Н связаны между собой некоторой функциональной зависимостью:

H = f(N),

а сама функция f является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N = 1, 2, ..., 6.

Процедура бросания кости:

- готовимся бросить кость. Исход опыта неизвестен, т.е. имеется некоторая неопределенность, обозначим ее Н1;

- кость брошена. Информация об исходе данного опыта получена, обозначим количество этой информации через I;

- обозначим неопределенность данного опыта после его осуществления через Н2.

За количество информации, которое получено в ходе осуществления опыта, примем разность неопределенностей "до" и "после" опыта:

I = H1–H2.

Очевидно, что в случае, когда получен конкретный результат, имевшаяся неопределенность снята (Н2=0). Количество полученной информации совпадает с первоначальной энтропией. Иначе говоря, неопределенность, заключенная в опыте, совпадает с информацией об исходе этого опыта. Значение Н2 могло быть и не равным нулю, например, в случае, когда в ходе опыта следующей выпала грань со значением, большим трех.

Следующим важным моментом является определение вида функции f. Если варьировать число граней N и число бросаний кости (обозначим эту величину через М). Общее число исходов (векторов длины М, состоящих из знаков 1, 2, ..., N) будет равно N в степени М:

X = N^m.

Так, в случае двух бросаний кости с шестью гранями имеем: Х = 6² = 36. Фактически каждый исход X есть некоторая пара (Х1, Х2), где Х1 и Х2 – соответственно исходы первого и второго бросаний (общее число таких пар – X).

Ситуацию с бросанием М раз кости можно рассматривать как некую сложную систему, состоящую из независимых друг от друга подсистем – "однократных бросаний кости". Энтропия такой системы в М раз больше, чем энтропия одной системы (так называемый "принцип аддитивности энтропии"):

f(N^m) = M * f(N),

где * – знак умножения.

Из приведенных формул выводится мера Хартли:

Н = log₂ N.

Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Н будет равно единице при N = 2. Иначе говоря, в качестве единицы измерения информации принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты при котором возможны два исхода: "орел", "решка").

В случае, когда вероятности различных исходов опыта не равновероятны (а имеют вероятности Р_i), меру энтропии вычисляют по формуле Шеннона:

.

В качестве примера определим количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке. Будем считать, что русский алфавит состоит из 33 букв и знака "пробел" для разделения слов. По формуле получаем: Н > 5 бит.