Ветвления и циклы в вычислительных алгоритмах

Составим алгоритм решения квадратного уравнения:

Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты а, b, с. Решением в общем случае будут два корня x₁ и х₂, которые вычисляются по формуле:

Все используемые в этой программе величины вещественного типа.

Слабость такого алгоритма – он не обладает важнейшим свойством, предъявляемым
к качественным алгоритмам, универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату
и завершать работу. Результатом может быть число, но может быть и сообщение о том, что при определенных данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Упомянутое свойство называют результатив-ностью алгоритма (в любом случае должен быть получен какой-то результат).

Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.

Решение уравнения зависит от значений коэффициентов a, b, с. Вот анализ рассмотренной выше задачи (ограничиваемся только поиском вещественных корней):

если a = 0, b = 0, с = 0, то любое х – решение уравнения;

если а = 0,b = 0, с ≠ 0,то уравнение действительных решений не имеет;

если а = 0, b ≠ 0, то это линейное уравнение, которое имеет одно решение х = -с/b;

если a ≠ 0 и d = b²- 4ас ≥ 0, то уравнение имеет два вещественных корня (формулы приведены выше);

если а ≠ 0 и d < 0, то уравнение не имеет вещественных корней.

Блок-схема алгоритма приведена на рис. 3.22.

Рис. 3.22. Блок-схема алгоритма решения квадратного уравнения

Этот же алгоритм на алгоритмическом языке:

В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий (рис. 3.23):

Рис. 3.23. Общий вид команды ветвления

Вначале проверяется условие (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется серия 1 – последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется серия 2 (отрицательная ветвь). В алгоритмических языках условие записывается после служебного словаесли, положительная ветвь – после словато, отрицательная – после словаиначе. Буквыкв обозначают конец ветвления.

Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений.

Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал):

На рис. 3.24 приведена блок-схема алгоритма. В нем используются три переменные целого типа: n – аргумент; i – промежуточная переменная; F – результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая n = 3.

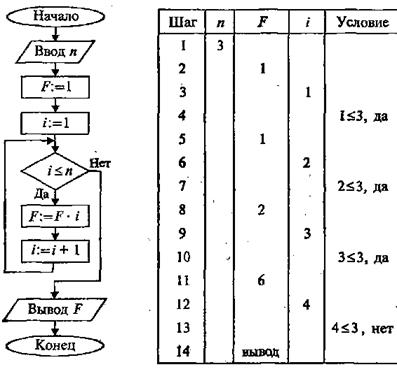
Рис. 3.24. Блок-схема алгоритма вычисления факториала

Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на алгоритмическом языке.

Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная командацикл-пока, или цикл с предусловием. Общий вид командыцикл-пока в блок-схемах и в алгорит-мических языках следующий (рис. 3.25):

Рис. 3.25. Общий вид командыцикл-пока

Запись алгоритма на алгоритмическом языке:

пока условие, повторять

нц

серия

кц

Выполнение серии команд (тела цикла) повторяется, пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение. Служебные слованц и кц обозначают начало цикла и конец цикла соответственно.

Цикл с предусловием (рис. 3.26) – это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции: если а = 0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных, и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля – еще один признак хорошего качества программы.

Рис. 3.26. Цикл с предусловием

В общем виде структурная командацикл с постусловием или цикл-до (рис. 3.27) представляется так:

Рис. 3.27. Структурная командацикл с постусловием

Здесь используется условие окончания цикла. Когда оно становится истинным, цикл закан-чивает работу.

Составим алгоритм решения следующей задачи: даны два натуральных числа М и N. Требует-ся вычислить их наибольший общий делитель – НОД(М, N).

Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M > N, то НОД(М, N) = НОД(М – N,N). Попробуйте самостоятельно доказать это свойство. Другой факт, лежащий в основе алгоритма, тривиален – НОД(М, M) = М. Для «ручного» выполнения этот алгоритм можно описать в форме следующей инструкции.

1. Если числа равны, то взять их общее значение в качестве ответа; в противном случае продолжить выполнение алгоритма.

2. Определить большее из чисел.

3. Заменить большее число разностью большего и меньшего значений.

4. Вернуться к выполнению пункта 1.

Блок-схема и алгоритм на алгоритмическом языке (рис. 3.28) будут следующими:

Рис. 3.28. Блок-схема и алгоритм Евклида

Алгоритм имеет структуру цикла с вложенным ветвлением.