Принцип причинности в квантовой механике

Из соотношения неопределенностей часто делают идеалистический вывод о непри­менимости принципа причинности к явле­ниям, происходящим в микромире. При этом основываются на следующих сообра­жениях. В классической механике, соглас­но принципу причинности — принципу классического детерминизма,по известно­му состоянию системы в некоторый момент времени (полностью определяется значе­ниями координат и импульсов всех частиц

системы) и силам, приложенным к ней, можно абсолютно точно задать ее состоя­ние в любой последующий момент. Следо­вательно, классическая физика основыва­ется на следующем понимании причинно­сти: состояние механической системы в начальный момент времени с известным законом взаимодействия частиц есть при­чина, а ее состояние в последующий мо­мент — следствие.

С другой стороны, микрообъекты не могут иметь одновременно и определенную координату, и определенную соответству­ющую проекцию импульса (задаются со­отношением неопределенностей (215.1)), поэтому и делается вывод о том, что в на­чальный момент времени состояние систе­мы точно не определяется. Если же со­стояние системы не определено в началь­ный момент времени, то не могут быть предсказаны и последующие состоя­ния, т. е. нарушается принцип причин­ности.

Необходимо, однако, отдавать себе отчет в том, что никакого нарушения принципа причинности применительно к микрообъектам не наблюдается, по­скольку в квантовой механике понятие состояния микрообъекта приобретает со­вершенно иной смысл, чем в классической механике. В квантовой механике состоя­ние микрообъекта полностью определяет­ся волновой функцией y(х, у, z, t), квад­рат модуля которой ½y(x, у, z, t)½² задает плотность вероятности нахождения части­цы в точке с координатами х, у, z.

В свою очередь, волновая функция y(х, у, z, t) удовлетворяет уравнению Шредингера (217.1), содержащему пер­вую производную функции y по времени. Это же означает, что задание функции y₀ (для момента времени to) определяет ее значение в последующие моменты. Следо­вательно, в квантовой механике начальное состояние y₀ есть причина, а состояние y в последующий момент — следствие. Это и есть форма принципа причинности в квантовой механике, т. е. задание функ­ции y₀ предопределяет ее значения для любых последующих моментов. Таким об­разом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествующего со­стояния, как того требует принцип при­чинности.

Движение свободной частицы

При движении свободной частицы (U(x)=0) ее полная энергия совпадает с кине­тической. Для свободной частицы, движу­щейся вдоль оси х, уравнение Шрединге­ра (217.5) для стационарных состояний примет вид

Прямой подстановкой можно убедиться в том, что частным решением уравнения (219.1) является функция y(х)=Ае^ikx, где А=const и k=const, с собственным зна­чением энергии

E=h²k²/(2m). (219.2)

Функция y(x)=Ae^ikx=Aе^(i/h)Ö2mEx представляет собой только координатную часть волновой функции y(х, t). Поэтому зависящая от времени волновая функция, согласно (217.4),

(здесь w=Е/h и k=p_x/h). Функция (219.3) представляет собой плоскую мо­нохроматическую волну де Бройля (см. 217.2)).

Из выражения (219.2) следует, что зависимость энергии от импульса

E=h²k²/(2m)=p²_x/(2m)

оказывается обычной для нерелятивист­ских частиц. Следовательно, энергия сво­бодной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значе­ния), т. е. ее энергетический спектр явля­ется непрерывным.

Таким образом, свободная квантовая частица описывается плоской монохрома­тической волной де Бройля. Этому соот­ветствует не зависящая от времени плот­ность вероятности обнаружения частицы

в данной точке пространства |y|² =yy**=|A|²,

причем одинаковая в любой его точке.

§ 220. Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками»

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высо­кими «стенками». Такая «яма» описывает­ся потенциальной энергией вида (для про­стоты принимаем, что частица движется вдоль оси х)

где l— ширина «ямы», а энергия отсчиты­вается от ее дна (рис. 296).

Уравнение Шредингера (217.5) для стационарных состояний в случае одно­мерной задачи запишется в виде

По условию задачи (бесконечно высокие «стенки»), частица не проникает за преде­лы «ямы», поэтому вероятность ее обнару­жения (а следовательно, и волновая фун­кция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0и х=l)непре­рывная волновая функция также должна обращаться в нуль. Следовательно, гра­ничные условия в данном случае имеют вид

y(0) =y(l)=0. (220.2)

В пределах «ямы» (0£x£l) уравне­ние Шредингера (220.1) сведется к урав­нению

Общее решение дифференциального уравнения (220.3):

y(х)=Аsinkx+Bcoskx.

Так как по (220.2) y(0)=0, то В=0. Тогда y(x)=Asinkx. (220.5)

Условие y(l)=Asinkl=0 (220.2) выпол­няется только при kl = np, где p — целые числа, т. е. необходимо, чтобы

k= np/l. (220.6)

Из выражений (220.4) и (220.6) следу­ет, что

Е_n=n²p²h²/2ml²(n=1,2,3,...), (220.7)

т. е. стационарное уравнение Шредингера, описывающее движение частицы в «по­тенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях E_n, зависящих от целого числа п. Следовательно, энергия E_n частицы в «потенциальной яме» с бес­конечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется.Квантованные значения энергии E_n называются уровнями энергии,а число n, определяющее энергетические уровни частицы, называется главным кван­товым числом.Таким образом, микрочасти­ца в «потенциальной яме» с бесконечно вы­сокими «стенками» может находиться толь­ко на определенном энергетическом уровне £„, или, как говорят, частица находится в квантовом состоянии п.

Подставив в (220.5) значение k из (220.6), найдем собственные функции:

Постоянную интегрирования А найдем из условия нормировки (216.3), которое для данного случая запишется в виде

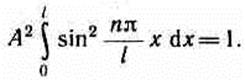
В результате интегрирования получим А=Ö2/1, а собственные функции будут иметь вид

Графики собственных функций (220.8), соответствующие уровням энер­гии (220.7) при n=1,2,3, приведены на рис. 297, а. На рис. 297, б изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная |y_n(x)|² = y_n(x) y*_n(x) для n=1, 2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n=2 частица не может находиться в сере­дине «ямы», в то время как одинаково часто может пребывать в ее левой и пра­вой частях. Такое поведение частицы ука­зывает на то, что представления о тра­екториях частицы в квантовой механике несостоятельны.

Из выражения (220.7) вытекает, что энергетический интервал между двумя со­седними уровнями равен

Например, для электрона при размерах ямы l=10^-1 м (свободные электроны

в металле) DEn»10^-35n Дж»10^-16n эВ, т.е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атом­ными (l»10^-10 м), то для электрона DEn»10^-17n Дж»10²n эВ, т.е. получа­ются явно дискретные значения энергии (линейчатый спектр). Таким образом, при­менение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высо­кими «стенками» приводит к квантован­ным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не наклады­вает.

Кроме того, квантово-механическое рассмотрение данной задачи приводит к выводу, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная p²h²/(2ml²). Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотно­шения неопределенностей. Неопределен­ность координаты Dx частицы в «яме» шириной l равна Dx=l. Тогда, согласно соотношению неопределенностей (215.1), импульс не может иметь точное, в данном случае нулевое, значение. Неопределен­ность импульса Dp»h/l. Такому разбросу значений импульса соответствует кинети­ческая энергия Emin»(Dp)²/(2m)=h²/(2ml²). Все остальные уровни (n>1) имеют энергию, превышающую это мини­мальное значение.

Из формул (220.9) и (220.7) следует, что при больших квантовых числах (n>>1) DE_n/E_n»2/n<<1, т.е. соседние уровни расположены тесно: тем теснее, чем боль­ше п. Если n очень велико, то можно говорить о практически непрерывной по­следовательности уровней и характерная особенность квантовых процессов — дискретность — сглаживается. Этот ре­зультат является частным случаем прин­ципа соответствия Бора(1923), согласно которому законы квантовой механики до­лжны при больших значениях квантовых чисел переходить в законы классической физики.

Более общая трактовка принципа со­ответствия,имеющего огромную роль в со­временной физике, заключается в следую­щем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения, причем в определенных предельных случаях новая теория перехо­дит в старую. Так, формулы кинематики и динамики специальной теории относи­тельности переходят при v<<c в формулы механики Ньютона. Например, хотя гипо­теза де Бройля приписывает волновые свойства всем телам, но в тех случаях, когда мы имеем дело с макроскопическими телами, их волновыми свойствами можно пренебречь, т. е. применять классическую механику Ньютона.