
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Необходимое и достаточное условие сходимости последовательности (через бесконечно малую последовательность)
|
|
Множество действительных чисел. Модуль действительного числа и его свойства.
Определение 1.Множеством действительных чисел называется совокупность всех рациональных и иррациональных чисел:  .
.
Определение 2.Действительным числом называется любая бесконечная периодическая или непериодическая дробь.
Действительные числа изображаются точками на числовой прямой и заполняют всю прямую без "дыр". Множество 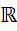 непрерывно.
непрерывно.
Свойство непрерывности R.Пусть  – произвольные множества из
– произвольные множества из 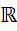 и
и  и
и 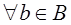 выполняется
выполняется  . Тогда
. Тогда 
 и
и 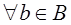 выполняется
выполняется  .
.
1. Модуль действительного числа и его свойства
Определение.Модулем действительного числа а называется неотрицательное число, обозначаемое |а|, определяемое формулой:

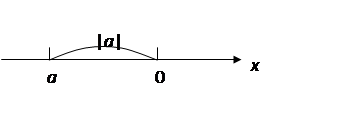 Геометрический смысл модуля: |
Геометрический смысл модуля: |  | –расстояние от точки 0 до точки а на числовой оси.
| –расстояние от точки 0 до точки а на числовой оси.
Из определения модуля вытекают его свойства.
Cвойства модуля:
1  . |a|=|-a|.
. |a|=|-a|.
2  . -|а|
. -|а| 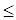 а
а 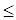 |а|.
|а|.
3  .
.  b
b  0 неравенство |х|
0 неравенство |х| 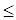 b равносильно -b
b равносильно -b 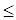 х
х 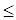 b (при b<0 неравенство |х|
b (при b<0 неравенство |х| 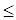 bне верно ни при каком х).
bне верно ни при каком х).
4  .
.  b
b  0 |х|³bÛ
0 |х|³bÛ  (если b<0, то неравенство верно для любого х).
(если b<0, то неравенство верно для любого х).
5  . (Неравенство треугольника) |а+b|
. (Неравенство треугольника) |а+b| 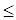 |а|+|b|
|а|+|b|
6  . |а-b|
. |а-b| 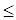 |а|+|b|
|а|+|b|
7  . |а-b|³|а|-|b|
. |а-b|³|а|-|b|
8  .|а+b|³|а|-|b|
.|а+b|³|а|-|b|
9  .
. 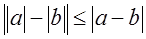
10 
 .
.
 .
.
11  .
. 
12  . 1)
. 1) 
2) 

2.Числовое множество. Примеры числовых множеств. Окрестности. Ограниченные и неограниченные числовые множества. Верхняя и нижняя грани числового множества. Достаточное условие существования верхней (нижней) грани множества.
Определение.
Числовое множество – множество, элементами которого являются действительные числа.
Примеры числовых множеств. 
1) Отрезок (сегмент, замкнутый промежуток)  .
.
2) Интервал (открытый промежуток)  .
.
3) Полуинтервалы 
1)-3) называются промежутками и обозначаются  .
.
4) Бесконечные промежутки:
 ,
,  ,
,
 ,
, 
 вся числовая прямая.
вся числовая прямая.
4. Окрестность точки
Пусть  .
.
Определение 1.Окрестностью точки а называется произвольный интервал, содержащий точку а. Обозначается V(a).
Определение 2.  -окрестностью точкиа называется интервал с центром в точке а ирадиусом
-окрестностью точкиа называется интервал с центром в точке а ирадиусом  . Обозначается V(a;e).
. Обозначается V(a;e).

V(a;e)=(a-e;a+e) или V(a;e)=  , V(a;e)=
, V(a;e)=  .
.
У каждой точки  существует бесконечно много
существует бесконечно много  -окрестностей.
-окрестностей.
Определение 3.Проколотой  -окрестностью точки а называется
-окрестностью точки а называется
 -окрестность без точки а. Обозначается
-окрестность без точки а. Обозначается 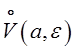
 .
. 
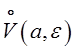

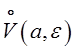 =
=  .
.
Определение 4.
 –
–  -окрестность точки +
-окрестность точки +  ,
,
 –
–  -окрестность точки -
-окрестность точки -  ,
,

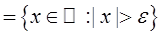 -
-  -окрестность точки
-окрестность точки  .
.
Определение 5.Односторонние окрестности точки а:
 –левая проколотая
–левая проколотая  -окрестностьточкиа,
-окрестностьточкиа,
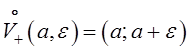 –праваяпроколотая
–праваяпроколотая  -окрестностьточки а.
-окрестностьточки а.

В дальнейшем будем рассматривать только  -окрестности. Будем называть их просто окрестностями.
-окрестности. Будем называть их просто окрестностями.
Ограниченные и неограниченные множества. Верхние и нижние грани числовых множеств
ПустьЕ – произвольное числовое множество,  .
.
Определение 1. Число  называется наименьшим (наибольшим) элементом множестваЕ, если
называется наименьшим (наибольшим) элементом множестваЕ, если  выполняется
выполняется  . Если Е имеет наибольший (наименьший) элемент, то он принадлежит множеству
. Если Е имеет наибольший (наименьший) элемент, то он принадлежит множеству  .
.
Определение 2.МножествоЕ называется ограниченным сверху, если  выполнено
выполнено 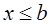 .
.
Определение 3.Число b называется верхней границей множества Е, если 
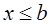 .
.
Очевидно, что если b – верхняя граница множестваЕ, то любое число, большее b, также будет верхней границей множества Е. Таким образом, ограниченное сверху множество имеет  множество верхних границ.
множество верхних границ.
Пример 1.  ограничено сверху. Одна из верхних границ – число 3. И любое число большее, чем 3 является верхней границей. Например,
ограничено сверху. Одна из верхних границ – число 3. И любое число большее, чем 3 является верхней границей. Например,  выполнено
выполнено  .
.
Определение 4.МножествоЕ называется ограниченным снизу, если  выполнено
выполнено  .
.
Определение 4.1.Число а называется нижней границей множества Е, если 
 .
.
Определение 5.МножествоЕнеограниченно сверху, если 
 .
.
Определение 6.Множество Енеограниченно снизу, если  :
:  .
.
Определение 7.МножествоЕ называется ограниченным, если оно ограничено и сверху, и снизу, то есть  выполнено
выполнено  .
.
Определение 7  .МножествоЕ называется ограниченным, если
.МножествоЕ называется ограниченным, если  выполнено
выполнено  .
.
Замечание.Определения 7 и 7  эквивалентны (равны).
эквивалентны (равны).
8.Множество  называется неограниченным, если
называется неограниченным, если  :
:  .
.
Определение 9.Верхней гранью множестваЕ (или точной верхней границей множества Е) называется наименьшая из всех верхних границ множества Е. Обозначается  (супремум) или
(супремум) или  .
.
Определение 9  .
.  1)
1)  выполнено
выполнено  ,
,
2)  .
.

Условие 2) можно заменить:  .
.
Определение 10.Нижней гранью множества Е (или точной нижней границей множества Е) называется наибольшая из всех нижних границ множества Е.
Обозначается m=infE (инфимум) или  .
.
infEможет как принадлежать так и не принадлежатьмножеству E.
Определение 10  .
.  1)
1)  выполнено
выполнено  ,
,
2)  .
.

Условие 2) можно заменить:  .
.
Условие 1) означает, что число mявляется нижней границей.
Условие 2) означает, что число m является наибольшей из нижних границ (то есть её нельзя увеличить).
Теорема. Всякое ограниченное сверху непустое множество имеет верхнюю грань. Всякое ограниченное снизу непустое множество имеет нижнюю грань.
Определение 11. Если множествоЕ не ограничено сверху, то  . Если множество Е не ограничено снизу, то
. Если множество Е не ограничено снизу, то 
3.Понятие числовой последовательности. Ограниченные и неограниченные последовательности. Возрастающие, убывающие, невозрастающие, неубывающие последовательности.
Определение 1.Если каждому натуральному числу nпо некоторому правилу поставить в соответствие некоторое число xn, то говорят, что определена числовая последовательность  Её обозначают:
Её обозначают:  или
или  .
.
Определение 2.Последовательность  называется ограниченнойсверху(снизу), если
называется ограниченнойсверху(снизу), если  выполняется
выполняется  .
.
Определение 3.Последовательность  называется неограниченной сверху (снизу), если
называется неограниченной сверху (снизу), если  >k (
>k (  <k).
<k).
Определение 4.Последовательность  называется ограниченной, если
называется ограниченной, если  выполнено
выполнено  .
.
Определение 5.Последовательность  называется неограниченной, если
называется неограниченной, если  :
:  .
.
Определение 6.Последовательность  называется возрастающей (убывающей), если
называется возрастающей (убывающей), если  выполнено
выполнено  (
(  ).
).
Определение 7.Последовательность  называется невозрастающей (неубывающей), если
называется невозрастающей (неубывающей), если  выполнено
выполнено  (
(  ).
).
Определение 8.Возрастающие и убывающие последовательности называются монотонными последовательностями.
4.Предел числовой последовательности, его геометрический смысл. Стационарная последовательность и ее предел. Единственность предела последовательности.
Пусть дана последовательность  :
:  (1)
(1)
Определение 1.Числоа называется пределом последовательности  , если
, если  выполнено
выполнено  . (2)
. (2)
Обозначается:  или
или  или
или  .
.
Если последовательность  имеет предел а, то она называется сходящейсяка.
имеет предел а, то она называется сходящейсяка.
Если последовательность  не имеет предела, то она называется расходящейся.
не имеет предела, то она называется расходящейся.
Определение 2. Последовательность  называется сходящейся, если
называется сходящейся, если  выполнено
выполнено  .
.
Геометрический смысл предела последовательности
Числоа является пределом последовательности  , если в любой e – окрестности точки а находятся все члены последовательности, начиная с некоторого (не принадлежит этой окрестности лишь конечное число членов).
, если в любой e – окрестности точки а находятся все члены последовательности, начиная с некоторого (не принадлежит этой окрестности лишь конечное число членов).

Стационарная последовательность - пос-ть, у которой все ее члены равны одному и тому же числу. ЕЕ предел равен этому числу.
Теорема 1.Любая сходящаяся последовательность  имеет только один предел.
имеет только один предел.
Доказательство.
 (От противного)Пусть
(От противного)Пусть 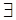 последовательность
последовательность  , которая имеет 2 предела:
, которая имеет 2 предела:  Тогда по определению предела
Тогда по определению предела

 ,
, 
 .
.
Обозначим  . Тогда
. Тогда  выполнено
выполнено  и
и  . Тогда
. Тогда  .
.
Получили, что положительное фиксированное число  меньше любого положительного числа
меньше любого положительного числа  (его можно брать сколь угодно малым), следовательноb-а=0 и значит, а=b.
(его можно брать сколь угодно малым), следовательноb-а=0 и значит, а=b.
Полученное противоречие доказывает теорему. 
5.Необходимое условие сходимости последовательности. Теорема о связях между последовательностями и их пределами (предельный переход в неравенствах, теорема о пределе промежуточной последовательности).
Теорема 2. (Необходимое условие сходимости) Всякая сходящаяся последовательность ограничена.
Пусть  сходящаяся последовательность, то есть
сходящаяся последовательность, то есть 
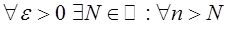 выполнено
выполнено  .
.
Доказательство.
 Пусть
Пусть  сходящаяся последовательность, то есть
сходящаяся последовательность, то есть 
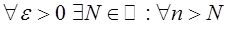 выполнено
выполнено  .
.

 .
.
Значит,  выполнено
выполнено  .
.
Обозначим М=  . Тогда "n
. Тогда "n 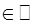 выполнено
выполнено  , то есть (по определению) последовательность
, то есть (по определению) последовательность  ограничена.
ограничена. 
Теорема 4.(предельный переход в неравенствах) Если  ,
,  и "n>N выполняется
и "n>N выполняется  , то
, то  .
.
Отметим, что из строгого неравенства не следует строгое, а следует нестрогое:  .
.
Теорема 5. (О пределе промежуточной последовательности)
Пусть  ,
,  ,
,  – последовательности, удовлетворяющие условию
– последовательности, удовлетворяющие условию
 "n>N0. (1)
"n>N0. (1)
Если  , то
, то  .
.
6.Понятие бесконечно малой последовательности, геометрический смысл. Свойства бесконечно малой последовательности.
Определение 1.Последовательность  называется бесконечно малой (БМП), если
называется бесконечно малой (БМП), если  .
.
Это означает, что  выполнено
выполнено  .
.
Геометрический смысл. Геометрически это означает, что в любой (сколь угодно малой) окрестности нуля находятся все члены последовательности  , начиная с некоторого номера
, начиная с некоторого номера  .
.
Теорема 1.Сумма любого конечного числа БМП есть БМП.
Теорема 2.Произведение БМП на ограниченную последовательность есть БМП.
Из теоремы 1 и 2 вытекают следствия.
Следствие 1.Если  БМП,
БМП,  , то
, то  – БМП.
– БМП.
Следствие 2.Разность двух БМП есть БМП.
Следствие 3. Произведение двух БМП есть БМП.
Следствие 4.Произведение БМП и сходящейся последовательности есть БМП.
Замечание 1. Случай произведения 2-х БМП последовательностей можно обобщить для любого конечного числа БМП.
Замечание 2. Для частного двух БМП аналогичное утверждение не верно, то есть если  ,
,  – БМП, то
– БМП, то  может и не быть БМП.
может и не быть БМП.
Необходимое и достаточное условие сходимости последовательности (через бесконечно малую последовательность).
Теорема 3.(Необходимое и достаточное условие сходимости последовательности) 
 , где
, где  – БМП, то есть
– БМП, то есть  .
.
Доказательство.
 1) Необходимость.
1) Необходимость.
Пусть  . Рассмотрим последовательность
. Рассмотрим последовательность  .
.
По определению предела  выполнено
выполнено  .
.
Следовательно, для последовательности 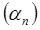 имеем:
имеем:  выполнено
выполнено  . Значит,
. Значит, 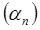 - БМП Þ
- БМП Þ  , где
, где  - БМП.
- БМП.
2) Достаточность. 
Пусть  , где
, где  .
.
По определению предела  выполнено
выполнено  . Так как
. Так как
 , то
, то  "n>NÞ
"n>NÞ  .
. 
8.Понятие бесконечно большой последовательности. Связь между бесконечно малой и бесконечно большой последовательностями.
Определение 1.Последовательность  называется бесконечно большой, если
называется бесконечно большой, если  выполняется
выполняется 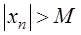 .
.
Для обозначения ББП используется запись  .
.
Теорема 1. 1) Если  – ББП, причем
– ББП, причем  то
то  – БМП;
– БМП;
2) если 
 – БМП и
– БМП и  то
то  – ББП.
– ББП.
9.Теоремы о пределе суммы, разности, произведения и частного сходящихся последовательностей.  . Неопределенности вида
. Неопределенности вида  ,
,  ,
,  ,
, 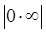 . Примеры.
. Примеры.
1. Частное  . 1)
. 1)  ,
,  .
.
2)  ,
,  .
.
3)  ,
,  .
.
4)  ,
,  (аналогично).
(аналогично).
5) 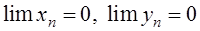 .
.
Отношение двух БМП. Это отношение может иметь предел (конечный или бесконечный), а может и не иметь предела в зависимости от конкретного способа задания последовательностей  и
и  . Поэтому отношение двух БМП называется неопределенностью вида
. Поэтому отношение двух БМП называется неопределенностью вида 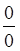 .
.
Если предел отношения найден или доказано, что он не существует, то говорят, что неопределенность раскрыта.
6) 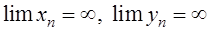
 – отношение двух ББП – неопределенность вида
– отношение двух ББП – неопределенность вида  .
.
2. Сумма  .
.
1)  ,
, 
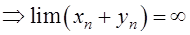 ,
,
2)  ,
, 
 ,
,
3)  ,
, 
 – неопределенность вида
– неопределенность вида  .
.
3. Произведение  .
.
1)  ,
, 
 ,
,
2)  ,
, 
 ,
,
3)  ,
,  – неопределенность вида
– неопределенность вида  .
.
1. 
2.  , где a>0.
, где a>0.
3. 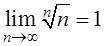 .
.
10.Понятие невозрастающей и неубывающей последовательности. Верхняя и нижняя грани последовательности. Теорема о пределе монотонной последовательности.
Определение 1.Верхней гранью последовательности  называется верхняя грань множества значений элементов этой последовательности.
называется верхняя грань множества значений элементов этой последовательности.
Обозначается
 .
.
Если множество значений элементов последовательности  ограничено сверху, то
ограничено сверху, то  есть число:
есть число:  Если множество значений неограниченно сверху, то
Если множество значений неограниченно сверху, то  .
.
Определение 2.Нижней гранью последовательности  называется нижняя грань множества значений этой последовательности.
называется нижняя грань множества значений этой последовательности.
Обозначается infxn.
Если множество значений элементов последовательности  ограничено снизу, то
ограничено снизу, то  . Если множество значений не ограничено снизу, то
. Если множество значений не ограничено снизу, то 
Теорема 1. 1) Любая неубывающая, ограниченная сверху последовательность имеет конечный предел.
2) Любая невозрастающая, ограниченная снизу последовательность имеет конечный предел.
Доказательство.
 1)
1)  - ограниченная сверху
- ограниченная сверху  .
.
Докажем, что  .
.
Выберем  . Тогда по определению 1' для этого e выполняется два условия:
. Тогда по определению 1' для этого e выполняется два условия:
1)  ,
,
2) 
Так как  - неубывающая, то
- неубывающая, то  .
.
Следовательно,  выполнены условия 1) и 2), значит,
выполнены условия 1) и 2), значит,  выполнено
выполнено  . Т. е.
. Т. е.  Þ
Þ 
 .
.
Итак, 
 :
:  выполняется
выполняется 
 .
.
Заметим, что из условия 1) следует, что  .
.
2) Доказывается аналогично.
Устанавливается, что  и, следовательно,
и, следовательно,  .
. 
11.Определение предела функции по Гейне и по Коши, их эквивалентность. Геометрический смысл предела функции.
Определение 1(по Гейне). ЧислоА называется пределом функции f(x) в точке а (или при х®а), если для любой последовательности (хn) точек из  , сходящейся к а, соответствующая последовательность значений функции (f(xn)) сходится к числу А.
, сходящейся к а, соответствующая последовательность значений функции (f(xn)) сходится к числу А.
Обозначается  или
или  .
.
Таким образом, 


 ,
,  выполнено (f(xn))
выполнено (f(xn))  A. Второе определение предела функции (по Коши).2. ЧислоА называется пределом функции f в точке а, если
A. Второе определение предела функции (по Коши).2. ЧислоА называется пределом функции f в точке а, если  >0
>0  >0:
>0:  : 0<
: 0<  <
<  выполнено
выполнено  .
.
Это определение называют определением предела “на языке 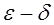 ”.
”.
Так как неравенство 0<  <
<  означает, что
означает, что 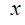
 , а неравенство
, а неравенство  - что
- что 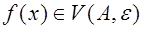 , то получаем определение “на языке окрестностей”.
, то получаем определение “на языке окрестностей”.
Теорема. Определения предела по Гейне и по Коши эквивалентны.
Итак, геометрический смысл предела функции состоит в следующем. ЧислоА является пределом функции f в точке а, если для любой, сколь угодно малой, e- окрестности точки А найдется d - окрестность точки а, такая что для всех х  соответствующие значения функции
соответствующие значения функции 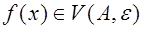 .
.
12.Односторонние пределы функции в точке. Необходимое и достаточное условие существования предела функции в точке (через односторонние пределы).
Односторонние пределы
Рассмотрим понятие предела функции  при стремлении
при стремлении 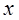 к точке
к точке  справа или слева. При этом
справа или слева. При этом  заменяется на
заменяется на  или на
или на  .
.
Обозначим через  левую окрестность точки а,
левую окрестность точки а,  – правую окрестность точки а.
– правую окрестность точки а.
Определение 1. (по Гейне) Число A называется левым (правым) пределомфункцииf(x) в точкеa, если  , соответствующая последовательность значений функции (f(xn)) сходится к A.Определение 2. (по Коши) ЧислоА называется левым (правым) пределом функции f(x) в точкеа, если
, соответствующая последовательность значений функции (f(xn)) сходится к A.Определение 2. (по Коши) ЧислоА называется левым (правым) пределом функции f(x) в точкеа, если 
 :
:  : a-d<x<a (a<x<a+d)выполняется неравенство
: a-d<x<a (a<x<a+d)выполняется неравенство  .
.
Обозначается  – левый предел,
– левый предел,  – правый предел.
– правый предел.
Определение 1 и определение 2 эквивалентны.Правый и левый предел функции в точке называются односторонними пределами в точке.
Теорема. Для того, чтобы функция f имела предел в точке aнеобходимо и достаточно, чтобы в этой точке существовали равные между собой односторонние пределы. При этом общее значение односторонних пределов равно пределу функции в точке а:

Доказательство.
 1) Необходимость.
1) Необходимость.
 и
и  . Это следует из определения предела и определения односторонних пределов.
. Это следует из определения предела и определения односторонних пределов.
2)Достаточность.
Пусть существуют односторонние пределы, равные А. Возьмем  . Тогда согласно определению 2
. Тогда согласно определению 2
 :
:  :
:  выполняется
выполняется  ,
,
 :
:  :
:  выполняется
выполняется  .
.
Выберем 
 :
:  :
:  выполняется
выполняется  .
.



 выполняется определение предела
выполняется определение предела  в точке а.
в точке а. 
13.Теорема о единственности предела функции. Теорема об ограниченности функции, имеющей предел в точке.
Теорема 1. (Единственность предела). Любая функция в точке может иметь только один предел.
Доказательство.
 Пусть
Пусть  ,
,  и
и  .
.
Возьмем (xn): xn  a. Рассмотрим (f(xn)). По определению предела функции по Гейне
a. Рассмотрим (f(xn)). По определению предела функции по Гейне  и
и  . Но по теореме о единственности предела последовательности отсюда следует, чтоА=В.
. Но по теореме о единственности предела последовательности отсюда следует, чтоА=В.
Полученное противоречие доказывает теорему. 
Теорема 2. Если  , то
, то  ограничена в некоторой проколотой окрестности точки а.
ограничена в некоторой проколотой окрестности точки а.
14.Теоремы о предельном переходе в неравенствах. Теоремы о пределе суммы, разности, произведения и частного функции.
Теорема 4. Пусть 1) 
 ;
;
2) 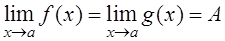 .
.
Тогда  .
.
Теорема 5. Пусть  ,
,  иА<B (A>B).
иА<B (A>B).
Тогда  :
:  :
:  выполняется
выполняется  (
(  ).
).
Теорема 6. Если 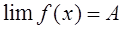 и А<B (A>B), то
и А<B (A>B), то  :
:  :
:  выполняется
выполняется  (
(  ).
).
Теорема 7. (Предельный переход в неравенствах)
Пусть 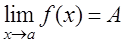 ,
,  и
и  :
:  :
:  выполняется
выполняется 
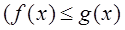 ). Тогда
). Тогда 
 .
.
Теоремы, связанные с арифметическими операциями над пределами
Теорема 8. Пусть  и
и  определены в некоторой проколотой окрестности точки а
определены в некоторой проколотой окрестности точки а  и
и 
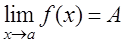 ,
,  . Тогда в точкеа существуют пределы суммы, разности, произведения и частного (при условии, что
. Тогда в точкеа существуют пределы суммы, разности, произведения и частного (при условии, что  и
и  в
в  ), причем
), причем
 ,
,
 ,
,
 ,
,
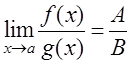 при
при  и
и  в
в  .
.
Доказательство.
 Докажем для суммы, остальное – аналогично.
Докажем для суммы, остальное – аналогично.
Возьмём  :
:  . Так как
. Так как 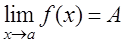 и
и  , то по определению предела функции по Гейне
, то по определению предела функции по Гейне  ,
,  . По теореме о пределе суммы последовательностей последовательность
. По теореме о пределе суммы последовательностей последовательность  также имеет предел, причем
также имеет предел, причем  .
.
Получили, что  :
:  последовательность
последовательность  сходится к числу А+В (
сходится к числу А+В (  )
) 
 .
. 
15.Виды неопределенностей. Примеры. Теорема о пределе сложной функции.
Бесконечные пределы и неопределенности
(дополнения к теореме 8 §6)
1.  ,
, 


2.  ,
, 


3. 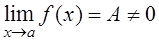 ,
, 


4.  ,
, 


5.  ,
, 

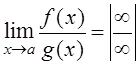
6.  ,
, 


7.  ,
, 


8.  ,
, 


9.  ,
, 

|
Просмотров 6348 |
|
|
