Решение системы дифференциальных уравнений 1-го порядка

Решение дифференциального уравнения n-го порядка.

7. Краевые задачи и методы их решения. Методы «стрельбы». Нелинейное уравнение краевой задачи и его решение методами половинного деления, Ньютона, секущих-хорд. Решение краевой задачи методом конечных разностей.

Общие сведения.

Многие задачи механики, физики, электротехники при математическом моделировании сводятся к решению дифференциальных уравнений. В дисциплине «Вычислительные методы» рассматриваются методы решения дифференциальных уравнений, которые особенно эффективны в сочетании с вычислительной техникой.

Рассмотрим основные понятия.

В зависимости от числа независимых переменных дифференциальные уравнения делятся на две категории:

‑ обыкновенные дифференциальные уравнения, содержащие одну независимую переменную;

‑ уравнения с частными производными, содержащие несколько независимых переменных.

Обыкновенные дифференциальные уравнения содержат одну или несколько производных от искомой функции

(*),

где ‑ независимая переменная.

Наивысший порядок входящей в уравнение производной называется порядком дифференциального уравнения.

‑ обыкновенное дифференциальное уравнение первого порядка;

‑ обыкновенное дифференциальное уравнение второго порядка.

Из общей записи дифференциального уравнения можно выразить старшую производную в явном виде: , .

Такая форма записи называется уравнением, разрешенным относительно старшей производной.

Линейным дифференциальным уравнением называется уравнение, линейное относительно искомой функции и ее производных. Например, ‑ линейное уравнение первого порядка.

Решением дифференциального уравнения называется всякая функция , которая при подстановке в уравнение превращает последнее в тождество.

Общее решение обыкновенного дифференциального уравнения -го порядка содержит произвольных постоянных , и имеет вид

.

Частное решение дифференциального уравнения получается из общего, если произвольным постоянным придать определенные значения.

Для уравнения первого порядка общее решение зависит от одной произвольной постоянной:

(**).

Если постоянная принимает определенное значение , то получим частное решение

.

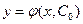Обозначим геометрический смысл дифференциального уравнения первого порядка. Поскольку производная характеризует наклон касательной к интегральной кривой в данной точке, то при из (*) получим ‑ уравнение линии постоянного наклона, называемой изоклиной. Меняя значение , получаем семейство изоклин.

Приведем геометрическую интерпретацию общего решения (**). Это решение описывает бесконечное семейство интегральных кривых с параметром , а частному решению соответствует одна кривая из этого семейства.

Для уравнений высших порядков геометрическая интерпретация более сложная. При через каждую точку проходит не одна кривая. Поэтому, для выделения частного решения из общего нужно задавать столько дополнительных условий, сколько произвольных постоянных в общем решении, т.е. каков порядок уравнения. Для уравнения второго порядка необходимо задать два дополнительных условия, благодаря которым можно найти значения двух произвольных постоянных.

В зависимости от способа задания дополнительных условий для получения частного решения дифференциального уравнения существуют два типа задач:

‑ задача Коши;

‑ краевая задача.

При этом в качестве дополнительных условий могут задаваться значения искомой функции и ее производных в некоторых точках.

В задаче Коши дополнительные условия называются начальными условиями и задаются в одной точке 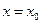(начальная точка).

Если же дополнительные условия задаются более чем в одной точке, то такая задача называется краевой. Сами дополнительные условия при этом называются граничными (или краевыми) условиями.

На практике обычно граничные условия задаются в двух точках и , которые являются границами решения дифференциального уравнения.

Методы решения задачи Коши.

Методы решения обыкновенных дифференциальных уравнений можно разбить на следующие группы: графические, аналитические, приближенные и численные.

Графические методы подразумевают геометрические построения. В частности метод изоклин применяется для решения дифференциальных уравнений первого порядка и основан на геометрическом определении интегральных кривых по заранее построенному полю направлений, определенному изоклинами.

Аналитические методы подразумевают получение решения в виде формул путем аналитических преобразований.

Приближенные методы используют различные упрощения самих уравнений путем обоснованного отбрасывания некоторых содержащихся в них членов.

Нас интересуют численные методы. Наиболее распространенным и универсальным численным методом решения дифференциальных уравнений является метод конечных разностей. Сущность его состоит в следующем. Область непрерывного изменения аргумента заменяется дискретным множеством точек, называемых узлами. Эти узлы составляют разностную сетку. Искомая функция непрерывного аргумента приближенно заменяется функцией дискретного аргумента на заданной сетке. Эта функция называется сеточной. Исходное дифференциальное уравнение заменяется разностным уравнением относительно сеточной функции. Такая замена дифференциального уравнения разностным называется его аппроксимацией на сетке (или разностной аппроксимацией). Таким образом, решение дифференциального уравнения сводится к отысканию значений сеточной функции в узлах сетки.

Важнейшие вопросы при решении дифференциального уравнения численным методом (при выборе того или иного метода):

1. Обоснованность замены дифференциального уравнения разностным.

2. Точность получаемых решений.

3. Устойчивость метода.

3. Одношаговые методы: Эйлера и его модификации, метод Рунге-Кутта.

Метод Эйлера.

Задача Коши: найти решение дифференциального уравнения

, (1)

удовлетворяющее начальному условию

. (2)

Геометрически: найти интегральную кривую, проходящую через заданную точку (рис. )

При решении задачи Коши на интервале , выбрав достаточно малый шаг , построим систему равноотстоящих точек:

. (3)

Для вычисления значения функции в точке разложим функцию в окрестности точки в ряд Тейлора:

. (4)

При достаточном малом значении членами выше второго порядка можно пренебречь, и с учетом получим следующую формулу для вычисления приближенного значения функции в точке :

. (5)

Рассматривая найденную точку как начальное условие задачи Коши, запишем аналогичную формулу для нахождения значения функции в точке

.

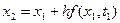Повторяя этот процесс, сформируем последовательность значений в точках 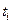по формуле:

. (6)

Процесс нахождения значений функции в узловых точках по формуле (6) называется методом Эйлера. Геометрическая интерпретация метода Эйлера состоит в замене интегральной кривой ломаной 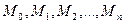с вершинами . Звенья ломаной Эйлера в каждой вершине имеют направление , совпадающее с направлением интегральной кривой уравнения (1), проходящей через точку (рис.). Последовательность ломаных Эйлера при 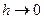на достаточно малом отрезке стремится к искомой интегральной кривой.

Рис. 7.2 Геометрическая интерпретация метода Эйлера

На каждом шаге решение определяется с ошибкой за счет отбрасывания членов ряда Тейлора выше первой степени, что в случае быстроменяющейся функции может привести к быстрому накапливанию ошибки. В методе Эйлера следует выбирать достаточной малый шаг .

Метод Эйлера является очень простым методом решения задачи Коши, но недостаточно точным: для его использования нужно выбирать достаточно маленький шаг интегрирования .

В связи с недостаточной точностью метода Эйлера для повышения точности используется его модификация.

При модифицированном методе Эйлера сначала вычисляют промежуточные значения

. (7)

после чего находят значение по формуле:

. (8)

Метод Рунге-Кутта.

Рассмотренные выше методы Эйлера (как обычный, так и модифицированный) являются частными случаями явного метода Рунге-Кутта -ro порядка. В общем случае формула вычисления очередного приближения методом Рунге-Кутта имеет вид:

. (9)

Функция приближает отрезок ряда Тейлора до -ro порядка и не содержит частных производных .