Основные типы и виды дифференциальных уравнений в частных производных

Ранее рассматривались обыкновенные дифференциальные уравнения. Их решения зависят лишь от одной переменной: , и т. д. Во многих практических задачах искомые функции зависят от нескольких переменных, и описывающие такие задачи уравнения могут содержать частные производные искомых функций. Они называются уравнениями с частными производными.

К решению дифференциальных уравнений с частными производными приводят, например, многие задачи механики сплошных сред. Здесь в качестве искомых функций обычно служат плотность, температура, напряжение и др., аргументами которых являются координаты рассматриваемой точки пространства, а также время.

Полная математическая постановка задачи наряду с дифференциальными уравнениями содержит также некоторые дополнительные условия. Если решение ищется в ограниченной области, то задаются условия на ее границе, называемые граничными (краевыми) условиями. Такие задачи называются краевыми задачами для уравнений с частными производными.

Если одной из независимых переменных в рассматриваемой задаче является время t, то задаются некоторые условия (например, значения искомых параметров) в начальный момент , называемые начальными условиями. Задача, которая состоит в решении уравнения при заданных начальных условиях, называется задачей Коши для уравнения с частными производными. При этом задача решается в неограниченном пространстве и граничные условия не задаются.

Задачи, при формулировке которых ставятся граничные и начальные условия, называются нестационарными (или смешанными) краевыми задачами. Получающиеся при этом решения меняются с течением времени.

Таким образом, математические модели физических и иных процессов описываются с помощью дифференциальных уравнений в частных производных. Аргументами функций этих уравнений являются пространственные координаты и время .

Уравнения первого порядка. Уравнения первого порядка называются также уравнениями переноса. Это объясняется тем, что такие уравнения описывают процессы переноса частиц в средах, распространения возмущений и т. п.

Его решение представляет интерес не только с практической точки зрения; в еще большей степени это уравнение полезно при разработке и исследовании разностных схем.

Будем считать, что искомая функция зависит от времени и одной пространственной переменной х. Тогда линейное уравнение переноса может быть записано в виде

.

Здесь ‑ скорость переноса.

Уравнения второго порядка. Линейным уравнением в частных производных второго порядка называется соотношение между функцией или и ее частными производными вида.

(1)

Если переменная функция зависит от и , то уравнение может быть записано следующим образом:

(2)

В случае если , то уравнения 1-2 называются однородными, иначе ‑ неоднородными.

Если , то уравнение (2) относится к классу эллиптических уравнений;

если , то ‑ это гиперболическое уравнение;

если ‑ параболическое уравнение.

Когда не имеет постоянного знака, получается уравнение смешанного типа.

К классическим эллиптическим уравнениям относятся:

- уравнение Лапласа , которое используется для описания магнитных и стационарных тепловых полей;

- уравнение Пуассона , которое применяется в электростатике, теории упругости и других науках;

- уравнение Гельмголъца , описывающее установившиеся колебательные процессы.

Оператор Лапласа:

в одномерном случае ;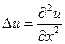

в двумерном случае ;

в трехмерном случае .

Среди гиперболических уравнений можно выделить:

Волновые уравнения:

одномерное 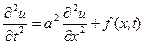, которое описывает вынужденные колебания струны;

двумерное , которое описывает колебания мембраны.

Телеграфное уравнение , которое описывает изменение потенциала в линиях электропередачи. Здесь 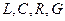- коэффициент самоиндукции, емкость, сопротивление, характеристика потерь на единицу длины линии.

К классическим параболическим уравнениям относится уравнение теплопроводности .

Для нахождения единственного решения дифференциального уравнения в частных производных необходимо задать начальные и граничные условия. Начальными условиями принято называть условия, заданные в начальный момент времени . Граничные условия задаются при различных значениях пространственных переменных. Для эллиптических уравнений задаются только граничные условия, которые можно разделить на три класса:

- условие Дирихле 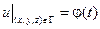- в этом случае на границе области Г, в которой ищется решение, задана некая непрерывная функция 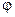. В одномерном случае это условие принимает вид: 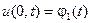и где - интервал, на котором ищется решение одномерной задачи;

- условие Неймана - в этом случае на границе области Г задана производная по направлению внешней нормали;

- смешанное условие .

Для параболических уравнений, кроме граничных условий, необходимо определить одно начальное, которое может быть таким: .

В случае гиперболических уравнений начальные условия могут быть следующими и .

Решение ряда дифференциальных уравнений в частных производных может быть получено аналитически. Одним из наиболее часто используемых методов является метод разделения переменных (метод Фурье). Рассмотрим этот метод подробнее.