Метод Рунге-Кутта четвертого порядка

Наиболее известным является метод Рунге-Kyттa четвертого порядка, расчетные формулы которого можно записать в виде:

(13)

4. Многошаговые методы: метод прогноза-коррекции Адамса, метод Милна.

Метод Адамса.

Многошаговые методы построены на том, что для вычисления значения применяются несколько предыдущих точек. При этом предыдущие несколько точек должны быть вычислены одношаговым методом (Эйлера, Рунге-Кутта).

Рассмотрим решение дифференциального уравнения

(14)

на интервале . Будем считать, что решение в точках уже найдено, и значения в этих точках будем использовать для нахождения значения .

Проинтегрируем уравнение (14) на интервале и получим соотношение:

(15)

При вычислении интеграла, входящего в (15), вместо функции будем использовать интерполяционный полином Лагранжа, построенный по точкам 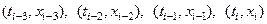. Подставив полином Лагранжа в (15), получаем первое приближение (прогноз) для значения функции в точке

. (16)

Как только вычислено, его можно использовать. Следующий полином Лагранжа для функции построим по точкам и новой точке 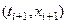, после чего подставляем его в (15) и получаем второе приближение (корректор):

. (17)

Таким образом, для вычисления значения 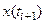методом Адамса необходимо последовательно применять формулы (16), (17), а первые четыре точки можно получить методом Рунге-Кутта.

Метод Милна.

Отличие метода Милна от метода Адамса состоит в том, что в качестве интерполяционного полинома используется полином Ньютона.

Подставив в (15) вместо функции интерполяционный полином Ньютона, построенный по точкам получаем первое приближение ‑ прогноз Милна для значения функции в точке :

. (18)

Следующий полином Ньютона для функции построим по точкам и новой точке , после чего подставляем его в (15) и получаем второе приближение ‑ корректор Милна:

. (19)

В методе Милна для вычисления значения необходимо последовательно применять формулы (18), (19), а первые четыре точки можно получить методом Рунге-Кутта.

Существует модифицированный метод Милна. В нем сначала вычисляется первое приближение по формуле (18), затем вычисляется управляющий параметр:

(20)

после чего вычисляется значение второго приближения ‑ корректор Милна ‑ по формуле:

(21)

В модифицированном методе Милна первые четыре точки можно получить методом Рунге-Кутта, а для вычисления значения необходимо последовательно применять формулы (18), (20), (21).

5. Решение системы дифференциальных уравнений 1-го порядка.

Ранее рассмотренные методы решения дифференциальных уравнений применимы и для систем дифференциальных уравнений. Рассмотрим метод Эйлера и Рунге-Кутта для решения систем.

Метод Эйлера.

Пусть требуется найти решение системы дифференциальных уравнений:

удовлетворяющее начальным условиям

Приближенные значения точного решения в точках вычисляются по формулам

Метод Рунге-Кутта.

Пусть дана система дифференциальных уравнений в матричном виде:

с начальным условием

.

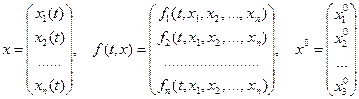Задавшись некоторым шагом и введя стандартные обозначения

, , , .

получим формулы для метода Рунге-Кутта для системы

6. Решение дифференциального уравнения n-го порядка.

7. Краевые задачи и методы их решения.

Ранее рассматривались задачи с начальными условиями, т. е. с условиями в одной (начальной) точке: при , . На практике приходится часто решать другого типа задачи, когда условия задаются при двух значениях независимой переменной (на концах рассматриваемого отрезка). Такие задачи, называемые краевыми, получаются при решении уравнений высших порядков или систем уравнений.

Методы решения краевых задач:

- точные аналитические методы;

- приближенные;

- численные.

Аналитические методы имеются лишь для решения узкого класса уравнений. В частности, хорошо развит этот аппарат для решения линейных дифференциальных уравнений второго порядка с постоянными коэффициентами, которые широко используются в исследовании различных физических процессов (например, в теории колебаний, динамике твердого тела и т. п.).

Приближенные методы разрабатывались еще задолго до появления вычислительных машин. Однако многие из них и до сих пор не утратили своего значения. Это методы коллокаций, наименьших квадратов и другие, основанные на минимизации невязок уравнений.

Нас интересуют численные методы. Численные методы можно разделить на две группы:

- сведение решения краевой задачи к последовательности решений задач Коши;

- непосредственное применение конечно-разностных методов.

8. Метод «стрельбы». Решение краевой задачи методами половинного деления, Ньютона.

Рассмотрим краевую задачу для уравнения второго порядка, разрешенного относительно второй производной:

(1)

Будем искать решение 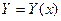этого уравнения на отрезке . Любой отрезок можно привести к этому отрезку с помощью замены переменной

.

Граничные условия на концах рассматриваемого отрезка

, . (2)

Сущность метода стрельбы заключается в сведении решения краевой задачи (1) с граничными условиями к решению задач Коши для того же уравнении (1) с начальными условиями

, . (3).

Здесь ‑ точка на оси ординат, в которой помещается начало искомой интегральной кривой; 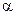угол наклона касательной к интегральной кривой в этой точке (рис.).

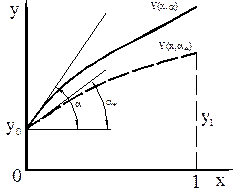
Считая решение задачи Коши зависящим от параметра , будем искать такую интегральную кривую которая выходит из точки и попадает в точку . Таким образом, если , то решение задачи Коши совпадает с решением краевой задачи. При учитывая второе граничное условие (2), получаем или

. (4)

Следовательно, получим уравнение вида , где . Это уравнение отличается от привычной записи тем, что функцию нельзя представить в виде некоторого аналитического выражения, поскольку она является решением задачи Коши (1), (3). Тем не менее для решения уравнения (4) может быть использован любой из рассмотренных ранее методов решения нелинейных уравнений.

Метод деления отрезка пополам.

Находим начальный отрезок , содержащий значение , на концах которого функция принимает значения разных знаков. Для этого решение задачи Коши должно при находиться ниже точки , a выше. Далее, полагая , снова решаем задачу Коши при и в соответствии с методом деления отрезка пополам отбрасываем один из отрезков: или , на котором функция не меняет знак, и т. д. Процесс поиска решения прекращается, если разность двух последовательно найденных значений 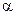меньше некоторого наперед заданного малого числа. В этом случае последнее решение задачи Коши и будет принято за искомое решение краевой задачи.

Описанный алгоритм называется методом «стрельбы», поскольку в нем как бы проводится «пристрелка» по углу наклона интегральной кривой в начальной точке. Следует отметить, что этот алгоритм хорошо работает в том случае, если решение 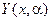не слишком чувствительно к изменениям 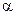; в противном случае мы можем столкнуться с неустойчивостью.

Одним из самых надежных является метод Ньютона. Он состоит в следующем. Пусть ‑ начальное приближение 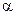, а ‑ искомое значение 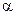. Решая задачу Коши при , находим . Тогда можем записать разложение в ряд с сохранением только линейных по членов:

.

Полагая 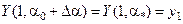, находим

. (5)

Производную в знаменателе этого выражения можно найти численно:

(6)

Здесь ‑ произвольное малое возмущение .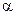

Для вычисления правой части (6) нужно решить задачу Коши при , в результате чего найдем значение . Вычисляя затем по формуле (5) поправку , находим следующее приближение параметра 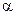: и т. д. Этот итерационный процесс продолжается до тех пор, пока очередное значение поправки по абсолютной величине не станет меньшим заданного малого числа .

Методы стрельбы могут также использоваться для решения системы уравнений.

10. Решение краевой задачи методом конечных разностей.

Достоинство этого метода состоит в том, что они сводят решение краевой задачи для дифференциального уравнения к решению системы алгебраических уравнений относительно значений искомой функции на заданном множестве точек. Это достигается путем замены производных, входящих в дифференциальное уравнение, их конечно-разностными аппроксимациями.

Рассмотрим сущность такого метода решения для дифференциального уравнения второго порядка (1) при заданных граничных условиях (2). Разобьем отрезок на равных частей точками . Решение краевой задачи (1), (2) сведем к вычислению значений сеточной функции , в узловых точках . Для этого напишем уравнение (1) для внутренних узлов:

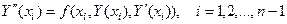(7)

Заменим производные, входящие в эти соотношения, их конечно-разностными аппроксимациями:

. (8)

Подставляя эти выражения в (7), получаем систему разностных уравнений

(9)

Выражение (9) является системой 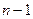алгебраических уравнений относительно значений сеточной функции . Входящие в данную систему (при ) и (при ) берутся из граничных условий.

Раздел. Дифференциальные уравнения в частных производных

Дифференциальные уравнения в частных производных

1. Основные типы и виды дифференциальных уравнений в частных производных. О методах решения дифференциальных уравнений в частных производных. Введение в сеточные методы. Понятия сетка, шаблон, слой. Построение разностных схем.

Решение дифференциальных уравнений с частными производными методом конечных разностей. Решение стационарных задач: уравнение Пуассона, уравнение Лапласа.

Уравнения в частных производных II-го порядка. Методы решения нестационарных задач. Вариационно-разностные методы решения уравнений в частных производных. Метод конечных элементов.