Классификация помехоустойчивых кодов

Коды Рида-Соломона (Reed-Solomon code, R-S code) — это недвоичные циклические коды, символы которых представляют собой m-битовые последовательности, где т — положительное целое число, большее 2. Код (n,к) определен на m-битовых символах при всех n и k, для которых

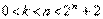(11.1)

где k - число информационных битов, подлежащих кодированию, а n - число кодовых символов в кодируемом блоке. Для большинства сверточных кодов Рида-Соломона (n, к)

(11.2)

где t - количество ошибочных битов в символе, которые может исправить код, а n-k = 2t- число контрольных символов. Расширенный код Рида-Соломона можно по­лучить при n = 2^m или n= 2^m+ 1, но не более того.

Код Рида-Соломона обладает наибольшим минимальным расстоянием, возмож­ным для линейного кода с одинаковой длиной входных и выходных блоков коде­ра. Для недвоичных кодов расстояние между двумя кодовыми словами определя­ется (по аналогии с расстоянием Хэмминга) как число символов, которыми отли­чаются последовательности. Для кодов Рила-Соломона минимальное расстояние определяется следующим образом.

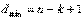(11.3)

Сверточные коды.Осо­бенностью линейного блочного кода, который описывается двумя целыми числами, n и k, и полиномиальным или матричным генератором является то, что каждый из n-кортежей кодо­вых слов однозначно определяется k-кортeжeм входного сообщения. Целое число к указывает на число бит данных, которые образуют вход блочного кодера. Целое число п - это суммар­ное количество разрядов в соответствующем кодовом слове на выходе кодера. Отношение k/n, называемое степенью кодирования кода (code rate), является мерой добавленной из­быточности. Сверточный код описывается тремя целыми числами n, k и К, где от­ношение k/n имеет такое же значение степени кодирования (информация, прихо­дящаяся на закодированный бит), как и для блочного кода; однако п не определяет длину блока или кодового слова, как это было в блочных кодах. Целое число К яв­ляется параметром, называемым длиной кодового ограничения (constrain! length); оно указывает число разрядов k-кортежа в кодирующем регистре сдвига. Важная осо­бенность сверточных кодов, в отличие от блочных, состоит в том, что кодер имеет память - n-кортежи, получаемые при сверточном кодировании, являются функци­ей не только одного входного k-кортежа, но и предыдущих К-1 входных k-кортежей. На практике nи к - это небольшие целые числа, а К изменяется с целью контроля мощности и сложности кода.

57. Границы Варшамова – Гильберта, Плоткина.

Нера́венство Ги́льберта — Варша́мова определяет предельные значения для параметров кодов (не обязательно линейных). Иногда употребляется название неравенство Гильберта — Шеннона — Варшамова, а в русскоязычной научной литературе — неравенство Варшамова — Гильберта.

Пусть

обозначает максимально возможную мощность q-чного кода C длины n и расстояния Хэмминга d (q-чным кодом является код с символами из поля , состоящего из q элементов).

Тогда

Когда q является степенью простого числа, можно упростить неравенство до , где k — наибольшее целое число, для которого .

Доказательство

Пусть C — код максимальной мощности при длине n и расстоянии Хэмминга d :

Тогда для любого существует по крайней мере одно кодовое слово , так что расстояние Хэмминга между x и cx удовлетворяет

потому как в противном случае мы могли бы расширить код с помощью слова x, оставив расстояние Хэмминга d неизменным, что противоречит предположению относительно максимальной мощности | C | .

Поэтому поле можно упаковать объединением множеств всех сфер радиуса d − 1 с центром в :

Объём каждого шара

потому что мы можем позволить (или выбрать) не более чем (d − 1)-му из n компонентов кодового слова принять одно из (q − 1) других возможных значений. Поэтому верно следующее неравенство

То есть

Грани́ца Пло́ткина — в теории кодирования определяет предел мощности двоичного кодa длины n и минимального расстояния d. Если существуют матрицы Адамара всех возможных порядков (что, однако, до сих пор ещё не доказано), то во всех частях теоремы выполняются равенства. Таким образом, граница Плоткина является точной в том смысле, что существуют коды, достигающие этой границы