
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Лемма Лоренца (запись в дифференциальной и интегральной формах). Теорема взаимности (получение из леммы Лоренца). Следствия, вытекающие из теоремы взаимности
|
|
Пусть в линейной изотропной среде имеются две независимые группы источников, одна из которых характеризуется сторонними электрическими токами 
Равенство (5.44) называют леммой Лоренца.
На основе леммы Лоренца доказывается теорема взаимности,. Предположим, что источники первой группы  сосредоточены в конечном объеме V1 а источники второй группы
сосредоточены в конечном объеме V1 а источники второй группы  -в конечном объеме V2. Области Vi и V2 пространственно разделены (не пересекаются
-в конечном объеме V2. Области Vi и V2 пространственно разделены (не пересекаются
друг с другом).
Интегрируя равенство (5.44) по произвольной области V, включающей в себя V1 и V2 (рис. 5.31), и применяя теорему Остроградского-Гаусса, получаем

где S - поверхность, ограничивающая объем V.
Соотношение (5.45) является интегральной формулировкой леммы Лоренца.

Распространим интегрирование в уравнении (5.45) на все пространство. При этом поверхность S уйдет в бесконечность. Не нарушая общностисти рассуждений, можно считать, что амплитуды векторов Ё1Н1, Ё2 и Н2 убывают с увеличением расстояния от источников быстрее, чем 1/r . Тогда при r→∞ левая часть уравнения (5.45) обратится в нуль. Кроме того, что по предположению вектор плотности сторонних токов  отличен от нуля только в объеме Vb а вектор
отличен от нуля только в объеме Vb а вектор  -только в объеме V2, получаем
-только в объеме V2, получаем 
В полученном выражении Ё1, - вектор напряженности электрического поля, создаваемого в точках объема V2 токами  распределенными в объеме V1 a E2- напряженность электрического поля, создаваемого в точках объема V1 токами, протекающими в объеме V2.
распределенными в объеме V1 a E2- напряженность электрического поля, создаваемого в точках объема V1 токами, протекающими в объеме V2.
Соотношение (5.46) является одной из формулировок теоремы взаимности.
Следствия, вытекающие из этой теоремы. Предположим, что объемы V1 и V2 и распределение токов 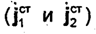 в них совершенно одинаковы. Из равенства (5.44) следует, что в этом случае векторы Ё1иЁ2 также будут одинаковыми. Например, пусть имеются две одинаковые антенны 1 и 2 с одинаковым, распределением токов. Тогда вне зависимости от того, является ли разделяющее антенны пространство однородным или нет, можно утверждать, что антенна 1 создает у антенны 2 такое же поле, какое антенна 2 создает у антенны 1. На основе теоремы взаимности можно также доказать, что диаграмма направленности приемной антенны имеет такую же форму, какую она имела бы, если бы антенна работала в качестве передающей. При доказательстве теоремы взаимности предполагалось, что среда, заполняющая рассматриваемое пространство, является линейной и изотропной. Предположим теперь, что среда, оставаясь линейной, является анизотропной. В этом случае параметры ε и μ (хотя бы один из них) будут тензорами.
в них совершенно одинаковы. Из равенства (5.44) следует, что в этом случае векторы Ё1иЁ2 также будут одинаковыми. Например, пусть имеются две одинаковые антенны 1 и 2 с одинаковым, распределением токов. Тогда вне зависимости от того, является ли разделяющее антенны пространство однородным или нет, можно утверждать, что антенна 1 создает у антенны 2 такое же поле, какое антенна 2 создает у антенны 1. На основе теоремы взаимности можно также доказать, что диаграмма направленности приемной антенны имеет такую же форму, какую она имела бы, если бы антенна работала в качестве передающей. При доказательстве теоремы взаимности предполагалось, что среда, заполняющая рассматриваемое пространство, является линейной и изотропной. Предположим теперь, что среда, оставаясь линейной, является анизотропной. В этом случае параметры ε и μ (хотя бы один из них) будут тензорами.
Тогда вместо уравнения (5.44) получаем

Переход от сферической волны к плоской. Свойства плоской волны в однородной изотропной среде (напряженность электрического поля плоской волны, действительная и мнимая части, параметра , их физический смысл).
Рассмотрим еще раз электромагнитное поле, создаваемое ЭЭВ в дальней зоне в безграничной однородной изотропной среде без потерь. Предположим, что векторы ЕиН требуется знать только в области V, размеры которой малы по сравнению с расстоянием до источника (r0). Введем дёкартову систему координат х, у, z, ось Z которой проведена .вдоль радиуса-вектора, соединяющего середину вибратора Q с точкой О, принятой за начало координат (рис.6.1). В пределах области V можно пренебречь изменением амплитуд векторов Ёт и Нт -и, кроме того, считать, что их фазы зависят только от координаты z, т.е. считать, что sin θ/r= = const, a exp(-ikr)=exp[-ik(ro+z)]. Вводя обозначение  (2λr0) =E0 перепишем формулы (5.20) в виде
(2λr0) =E0 перепишем формулы (5.20) в виде


В (6.1) учтено, что векторы Ёт и Нт перпендикулярны друг другу и направлению распространения волны (оси Z). Ориентация векторов Ёт и Нт относительно осей X и У зависит от ориентации вибратора, создающего поле. В общем случае эти векторы могут иметь как х-ю, так и у-ю составляющие, связанные соотношениями

Поверхности равных фаз (ПРФ) в данном случае определяются уравнением z = const, т.е. представляют собой плоскости, перпендикулярные оси Z. Волну, ПРФ которой образуют семейство параллельных плоскостей, называют плоской волной. Таким образом, сферическую волну, создаваемую ЭЭВ, в пределах области V можно рассматривать как плоскую волну.
Очевидно, аналогичный результат получится и в тех случаях, когда источником поля являются элементарный магнитный вибратор, элемент Гюйгенса, система таких излучателей и др. При этом в общем случае между составляющими вектора Ёо по осям X и У может иметь место фазовый сдвиг.
Свойства плоской волны в однородной изотропной среде
Исследуем основные свойства плоской волны, распространяющейся в безграничной однородной изотропной среде. Источники, создающие волну, находятся за пределами рассматриваемой области. Поэтому векторы Ёт и Нт удовлетворяют однородным уравнениям Гельмгольца (2.33) и (2.34) соответственно. Предположим, что поле не зависит от координат х и у. Тогда уравнения (2.33) и (2.34) принимают вид



Рассматривая таким же образом фазу напряженности электрического поля волны 2), придем к равенству ω∆t=-β∆z. В этом случае положительным ∆t соответствуют отрицательные значения ∆z, то есть волна 2) распространяется противоположно оси Z.
Предположим, что источник, создающий электромагнитное поле, расположен со стороны отрицательных значений z (рис. 6.1). Так как среда считается безграничной и однородной, в рассматриваемой области пространства должна существовать только волна, распространяющаяся в положительном направлении оси Z. Поэтому в первом слагаемом в формуле (6.4) в соответствии с выбором вида множителя exp(-i kz) следует положить

В среде без потерь  и формулы (6.13) переходят в (6.1).
и формулы (6.13) переходят в (6.1).
При изменении удельной проводимости от нуля до бесконечности угол ψсувеличивается от нуля до π/4, а модуль Zc убывает от 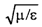 до нуля. Как видно, наличие потерь приводит к уменьшению абсолютной, величины характеристического сопротивления, т.е. к увеличению | Н | при заданном значении | Е |. Это обусловлено тем, что величина Нопределяется как током проводимости, так и током смещения. В среде без потерь существуют только токи смещения. В среде с потерями при тех же значениях Е и ε токи смещения остаются прежними, но к ним добавляются токи проводимости.
до нуля. Как видно, наличие потерь приводит к уменьшению абсолютной, величины характеристического сопротивления, т.е. к увеличению | Н | при заданном значении | Е |. Это обусловлено тем, что величина Нопределяется как током проводимости, так и током смещения. В среде без потерь существуют только токи смещения. В среде с потерями при тех же значениях Е и ε токи смещения остаются прежними, но к ним добавляются токи проводимости.
Проанализируем полученные результаты. Рассмотрим сначала случай, когда вектор. Ёm имеет лишь одну составляющую, например, Ёхт. Тогда вектор Нт также будет иметь одну составляющую, перпендикулярную Ет (в рассматриваемом примере Нут). Считая вектор Ёо вещественным (Ё0=х0Е0) и переходя к мгновенным значениям векторов Е и Н из (6:13) получаем

Из полученных формул видно, что поле плоской волны в однородной изотропной среде обладает следующими свойствами.
Волна является поперечной. Комплексные амплитуды (Ёт и Нт) векторов Е и Н всегда взаимно перпендикулярны, а в частном случае, когда вектор Ёо имеет одну составляющую (например, Ёо =хоEо), взаимно перпендикулярны и их мгновенные значения. Более подробно вопрос о перпендикулярности мгновенных значений векторов Е и Н рассмотрен в 6.2. Поверхности равных фаз определяются уравнением z = const и представляют собой семейство плоскостей, перпендикулярных оси Z. Амплитуды векторов Е и Н экспоненциально убывают вдоль оси Z. Постоянную а называют коэффициентом ослабления. В среде без потерь α= 0 и

амплитуды векторов Е и Н не зависят от координат. При σ≠0 поверхности равных амплитуд (ПРА) совпадают с ПРФ. Волны, обладающие таким свойством, как и волны, амплитуды векторов Е и Н которых не зависят от координат, называют однородными. При
σ≠0 между векторами Е и Н имеется фазовый сдвиг. Вектор Нопаздывает по фазе относительно вектора Е на угол  В среде без потерь векторы Е и Н изменяются синфазно. При изменении а от нуля до бесконечности фазовый сдвиг возрастает от нуля до π/4. На рис. 6.2 и 6.3 показаны зависимости мгновенных значений векторов Е и Н от времени tв некоторой фиксированной точке пространства (z = z0) в среде с σ≠0 (см. рис. 6.2) и в среде без потерь (см. рис.6.3). На рис.6.4 и 6.5 показаны зависимости тех же величин от координаты z в некоторый фиксированный момент
В среде без потерь векторы Е и Н изменяются синфазно. При изменении а от нуля до бесконечности фазовый сдвиг возрастает от нуля до π/4. На рис. 6.2 и 6.3 показаны зависимости мгновенных значений векторов Е и Н от времени tв некоторой фиксированной точке пространства (z = z0) в среде с σ≠0 (см. рис. 6.2) и в среде без потерь (см. рис.6.3). На рис.6.4 и 6.5 показаны зависимости тех же величин от координаты z в некоторый фиксированный момент
времени t=t0 для случаев σ≠0 (см.рис.6.4) и σ =0 (см. рис. 6.5).
Фазовая скорость vф плоской волны находится так же, как в случае сферической волны (см.5.3). Используя формулу (6.13), рассмотрим перемещение ∆z ПРФ за время ∆t. В результате придем к равенству 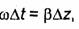 из которого следует, что при σ≠0
из которого следует, что при σ≠0


В среде без потерь  т.е. равна скорости света в среде с теми же параметрами ε и μ. Так как
т.е. равна скорости света в среде с теми же параметрами ε и μ. Так как  то vф в среде с потерями меньше уф в среде без потерь с теми же ε и μ.
то vф в среде с потерями меньше уф в среде без потерь с теми же ε и μ.
Параметр β, определяющий фазовую скорость, называют коэффициентом фазы. Как видно из (6.16), при σ≠0 фазовая скорость зависит от частоты (tg δ =σ/(ωε)): с увеличением последней она возрастает. Предельное значение vфпри ω→∞ равно
 Кроме того, величина vф зависит от проводимости среды: при одинаковой частоте она будет меньше в среде с большей проводимостью.
Кроме того, величина vф зависит от проводимости среды: при одинаковой частоте она будет меньше в среде с большей проводимостью.

Она меньше длины волны в среде без потерь с теми же ε и μ. Ее значение зависит от проводимости среды. При фиксированной частоте длина волны λ убывает с увеличением σ; при σ = О длина волны 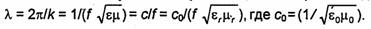
Распространение волны сопровождается переносом энергии. При σ≠0 комплексный вектор Пойнтинга

содержит как действительную, так и мнимую часть. Это означает, что имеется как активный, так и реактивный поток энергии. Средняя за период плотность потока энергии экспоненциально убывает вдоль оси Z:

При σ≠0 комплексный вектор Пойнтинга является чисто действительным и не зависит от координат:

Как видно, в этом случае имеется только активный поток энергии.
Возникновение реактивного потока энергии в среде с σ≠0 может быть объяснено следующим образом. При распространении электромагнитной волны в среде возникают электрические токи с плотностью j = σЕ, на поддержание которых расходуется часть энергии волны. В свою очередь, возникшие в среде электрические токи, излучают электромагнитное поле: создают вторичную плоскую волну, которая складывается с первичной, происходит непрерывный обмен энергией между волной и средой, что и приводит к возникновению реактивного потока энергии.
Скороcть распространения энергии вычисляется по формуле (1.162) и равна фазовой скорости:

Как видно, при σ≠0 скорость распространения энергии зависит от частоты. В среде без потерь  одинакова при любой частоте.
одинакова при любой частоте.
Характеристическое сопротивление волны Zc при σ≠0 также
зависит от частоты. Модуль Zc возрастает с увеличением f. Его
предельное значение при f→∞ совпадает с характеристическим сопротивлением волны, распространяющейся в среде без потерь с теми же ε и μ, т.е. равно  Аргумент характеристического сопротивления ψс изменяется от π/4 (при f→0 ) до нуля (при f→∞).
Аргумент характеристического сопротивления ψс изменяется от π/4 (при f→0 ) до нуля (при f→∞).
Из изложенного следует, что свойства плоской волны, распространяющейся в среде с проводимостью и в среде без потерь, различны. Основное отличие состоит в том, что в среде без потерь параметры плоской волны (vф, v3, a, Zc и др.) одинаковы при любых частотах, а в среде с проводимостью они зависят от частоты. Зависимость свойств волны от частоты называется дисперсией, а соответствующие среды - диспергирующими. Отметим, что среда может быть диспергирующей и при σ = 0, если характеризующие ее параметры е и ц зависят от частоты.
В общем случае вектор Ёт имеет две составляющие Ёхт и Ёут, между которыми возможен фазовый сдвиг. При этом вектор Нт также будет иметь две составляющие Нхт и Нут. Если составляющие вектора E по осям X и Y (Ех и Eу) изменяются синфазно, то поворотом осей координат X и У вокруг оси Z этот случай сводится к уже рассмотренному, когда вектор Ёт имеет одну составляющую. При наличии между составляющими Ёхт и Ёут фазового сдвига, не равного nπ, где п - целое число, волна имеет некоторые особенности, например при f→0 мгновенные значения векторов Е и Н не являются взаимно перпендикулярными (см.6.2). Перечисленные выше остальные свойства плоской волны имеют место и в этом случае.
Рассмотрим два частных случая реальных сред: диэлектрики и проводники.
22. Свойства плоской волны в однородной изотропной среде (волновое сопротивление, форма незатухающей и затухающей плоской волны, комплексный вектор Пойнтинга). Плоские волны в проводниках. Глубина проникновения.
Волны в диэлектриках
В диэлектриках tgδ<<1, поэтому можно приближенно положить  Применяя дважды это приближенное равенство к выражению (6.7), получаем
Применяя дважды это приближенное равенство к выражению (6.7), получаем

Из полученных результатов следует, что параметры волны (β,λ,vф,vэ,Zc), распространяющейся в реальном диэлектрике, мало отличаются от ее параметров в среде без потерь с теми же ε и μ. Коэффициент ослабления α является малой величиной и в первом приближении не зависит от частоты. Дисперсионные свойства проявляются незначительно.
6.1.4. Волны в проводниках
В проводниках (например, в металлах) tg 5>> 1. Поэтому в выражениях для α и β можно пренебречь единицей по сравнению с tg 5. В результате получим

6.1.5. Затухание волн
Коэффициент ослабления α волны, распространяющейся в проводнике, большая величина. Поэтому амплитуды векторов поля резко уменьшаются вдоль направления распространения: волна быстро затухает. Пусть амплитуда напряженности электрического поля в точке с координатой z равна Ет (z), а амплитуда в точке с координатой z + l равна Em(z + I). Отношение
Em(z)/Em(z +l )= ехр(αl) (6.30)
показывает, во сколько раз уменьшилась амплитуда волны при прохождении ею расстояния l.
Затухание измеряют в неперах (Нп) и децибелах (дБ). Затухание в неперах определяют как натуральный логарифм отношения (6.30) In [Em (z)IEm (z + l)]= αl Затухание в децибелах определяют как двадцать десятичных логарифмов того же отношения:  Коэффициент α, таким образом, определяет затухание волны при прохождении ею пути в один метр и измеряется в неперах на метр (Нп/м).
Коэффициент α, таким образом, определяет затухание волны при прохождении ею пути в один метр и измеряется в неперах на метр (Нп/м).
Вычислим затухание волны, распространяющейся в меди, при частоте в 1 Мгц. Коэффициент ослабления 
 Это означает, например,
Это означает, например,
что при прохождении волной расстояния в один миллиметр ее амплитуда уменьшается в е14,8 раз, т.е. примерно в 2,67 миллиона раз. Приведенный пример показывает, что переменное электромагнитное поле на частотах радиотехнического диапазона практически не проникает в глубь проводника.
6.1.6. Глубина проникновения
Расстояние ∆°, при прохождении которого электромагнитное поле ослабевает в е раз, называют глубиной проникновения поля в среду. На расстоянии ∆° ослабление составляет 1 Нп, т.е. α∆° = 1 и, следовательно,

Как видно из формулы (6.32), глубина проникновения зависит от частоты: чем больше частота, тем меньше ∆°.
23. Падение нормально поляризованной плоской волны на границу раздела двух сред (преломление, отражение волн, законы Снеллиуса, коэффициенты отражения и прохождения световой волны).
Пусть линейно поляризованная плоская электромагнитная волна падает на плоскую бесконечно протяженную границу раздела двух однородных изотропных сред, характеризуемых параметрами 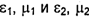 соответственно. Введем прямоугольную систему координат х, у, zтак, чтобы плоскость YOZсовпадала с поверхностью раздела, а плоскость падения - с плоскостью XOZ. Угол φ между направлением распространения волны и нормалью к поверхности раздела будем называть углом падения (рис. 7.2).
соответственно. Введем прямоугольную систему координат х, у, zтак, чтобы плоскость YOZсовпадала с поверхностью раздела, а плоскость падения - с плоскостью XOZ. Угол φ между направлением распространения волны и нормалью к поверхности раздела будем называть углом падения (рис. 7.2).
В выбранной системе координат направляющие косинусы, определяющие направление распространения волны,


Отметим, что постоянная Ёо равна значению комплексной амплитуды у-й составляющей напряженности электрического поля в начале координат (при x = z=0). Соответственно векторная постоянная Ёо = у0Ёоравна значению комплексной амплитуды вектора Е в начале координат.
Из физических соображений очевидно, что падающая волна может частично (или полностью) отразиться от границы раздела (х = 0) и частично (или полностью) пройти во вторую среду. Естественно предположить, что отраженная и преломленная волны будут плоскими.
Если, исходя из этого предположения, удастся найти поле, удовлетворяющее граничным условиям

где  - касательные составляющие векторов Ё и Н в первой и во второй средах соответственно, то это поле будет решением рассматриваемой задачи.
- касательные составляющие векторов Ё и Н в первой и во второй средах соответственно, то это поле будет решением рассматриваемой задачи.
Граничные условия (7.7) должны выполняться на всей плоскости х = 0, т.е. при любых значениях переменных у и z. Так как поле падающей волны (7.6) не зависит от переменной у, то необходимо предположить, что поле отраженной и преломленной волн также не зависит от координаты у. Это означает, что векторы, определяющие направление распространения отраженной и преломленной волн, параллельны плоскости XOZ. Можно также предположить, что отраженная и преломленная волны являются нормально поляризованными (рис.7.3). С учетом сделанных предположений выражения для векторов поля отраженной волны  могут быть получены из формул (7.6), если в последних заменить
могут быть получены из формул (7.6), если в последних заменить  -угол между осью Xи направлением распространения отраженной волны (см. рис.7.2 и 7.3), a
-угол между осью Xи направлением распространения отраженной волны (см. рис.7.2 и 7.3), a  - некоторая, пока неизвестная постоянная, равная значению комплексной амплитуды у-й составляющей напряженности электрического поля отраженной волны. Обычно вместо угла φ' рассматривают угол φ1=π-φ’, называемый
- некоторая, пока неизвестная постоянная, равная значению комплексной амплитуды у-й составляющей напряженности электрического поля отраженной волны. Обычно вместо угла φ' рассматривают угол φ1=π-φ’, называемый
углом отражения. Так как  При этом
При этом 
характеристическое сопротивление волны во второй среде, а  -некоторая, постоянная, равная значению комплексной амплитуды у-й составляющей напряженности электрического поля преломленной волны. Ориентация векторов Ёт и Нт падающей, отраженной и преломленной волн показана на рис.7.3. Углы φ1и θ так же, как и постоянные
-некоторая, постоянная, равная значению комплексной амплитуды у-й составляющей напряженности электрического поля преломленной волны. Ориентация векторов Ёт и Нт падающей, отраженной и преломленной волн показана на рис.7.3. Углы φ1и θ так же, как и постоянные  подлежат определению.
подлежат определению.
Граничные условия (7.7) должны выполняться при всех значениях координаты г. Это возможно только, в том случае, если зависимость векторов Ё и Н от переменной z во всех трех волнах будет одинаковой. Поэтому необходимо, чтобы

Так как углы φ и φ1заключены в интервале [0, π/2], то из
равенства (7.10) следует первый закон Снеллиуса φ = φ1("Угол
падения равен углу отражения"). Из равенства (7.11) вытекает
соотношение sin θ/sinφ = k1/k2, которое в случае идеальных
однородных изотропных сред выражает второй закон Снеллиуса
("Отношение синуса угла преломления к синусу угла падения равно относительному показателю преломления сред n12"). Действительно, коэффициент преломления среды п = c0 /c, где с0 =

Для определения постоянных А и В используем граничные условия (7.7). Так как поле в первой среде складывается из полей падающей и отраженной волн, а поле во второй среде совпадает с полем преломленной волны, то формулы (7.7) принимают вид
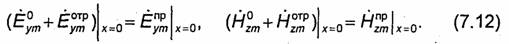
Подставляя в эти выражения значения соответствующих составляющих комплексных амплитуд напряженности электрического и магнитного полей и учитывая равенства (7.10) и (7.11), приходим к соотношениям

где  - коэффициенты отражения и прохождения соответственно. Их также часто называют коэффициентами Френеля
- коэффициенты отражения и прохождения соответственно. Их также часто называют коэффициентами Френеля
-Падение плоской волны на границу поглощающей среды. Действительный угол преломления.
Падение плоской волны на границу поглощающей оптически более плотной среды.
Пусть плоская волна падает под углом φ на плоскую границу раздела двух сред, из которых первая - идеальный диэлектрик, а вторая обладает проводимостью. Общие формулы, определяющие поля падающей, отраженной и преломленной волн, можно использовать и в этом случае, если считать в них параметры k2и Zc2 комплексными величинами. Из второго закона Снеллиуса (7.11) следует, что при этом sin 8 становится комплексным, так как k1и sinφ - действительные числа, а k2 = k2комплексная величина.
Это означает, что параметр θ нельзя рассматривать как геометрический угол, под которым распространяется преломленная волна. Введем обозначения

и х = const соответственно. Следовательно, волна (7.46) является неоднородной плоской волной. Направление распространения этой волны образует некоторый угол θД с осью X, который называют истинным (или действительным) углом преломления (рис.7.7). Поверхности равных фаз представляют собой параллельные плоскости, нормаль к которым образует с осями X и Zуглы θд и π/2-θд соответственно. Уравнение,

определяющее такие плоскости, может быть также записано в виде х cosθД+ zsinθД = const. Сравнивая это равенство с уравнением (7.47), находим, что
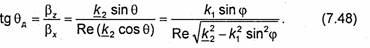
Отметим, что в рассматриваемом случае ПРФ повернуты относительно ПРА на угол θД (см. рис.7.7).
Амплитуды векторов Е и Н экспоненциально убывают в направлении нормали к поверхности раздела (вдоль оси X). Имеется продольная по отношению к направлению распространения преломленной волны составляющая вектора Н(в случае нормальной поляризации) или продольная составляющая вектора Е (в случае параллельной поляризации).
Поле в первой среде складывается из падающей и отраженной волн и не имеет принципиальных отличий от поля, возникающего при отражении волны от границы раздела двух диэлектриков.
Аналогичные результаты можно получить, анализируя случай параллельной поляризации.
Практически важным является случай, когда вторая среда оптически намного плотнее первой:

Это означает, что при любом угле падения ср на поверхность хорошо проводящей среды преломленная волна распространяется практически вдоль нормали к поверхности раздела. Поверхности равных фаз и поверхности равных амплитуд при этом практически совпадают, и волну можно считать однородной. Продольная по отношению к направлению распространения составляющая вектора Н (или, в случае параллельной поляризации, вектора Ё)будет пренебрежимо мала по сравнению с поперечной составляющей. Можно считать, таким образом, что волна является поперечной, причем векторы Е и Н, в ней сдвинуты по фазе друг относительно друга на угол  Иными словами, при анализе плоской волны, возникающей в результате преломления на поверхности хорошо проводящей среды, можно использовать все основные соотношения, полученные в 6.1.4 при исследовании свойств плоской волны, свободно распространяющейся в хорошо проводящей безграничной однородной изотропной среде.
Иными словами, при анализе плоской волны, возникающей в результате преломления на поверхности хорошо проводящей среды, можно использовать все основные соотношения, полученные в 6.1.4 при исследовании свойств плоской волны, свободно распространяющейся в хорошо проводящей безграничной однородной изотропной среде.
Подчеркнем, что амплитуды векторов Е и Н преломленной волны в металле быстро убывают с удалением от границы раздела и волна фактически существует лишь в тонком слое вблизи поверхности раздела.
24 Приближенные граничные условия Леонтовича-Щукина (вывод и запись условия).
Задача определения поля в присутствии металлических тел с конечной проводимостью имеет большое значение. Ее решение часто можно упростить введением приближенных граничных условий Леонтовича-Щукина. В отличие от обычных граничных условий, связывающих значения составляющих поля на границе раздела в разных средах, граничные условия Леонтовича-Щукина
выражают связь между составляющими векторов Ё и Н в одной среде.
В 7.6 было показано, что при выполнении условия (7.49) плоская волна, падающая под любым углом ср на границу раздела двух сред, возбуждает во второй среде плоскую волну, распространяющуюся практически вдоль нормали к поверхности раздела. Так как ПРФ и ПРА такой волны практически совпадают, то ее можно считать однородной. При этом должны выполняться соотношения

где п0-единичная нормаль, внешняя к плотной среде.

Соотношение (7.52) называют приближенным граничным условием Леонтовича-Щукина. Из него следует, что на поверхности реального проводника касательная составляющая напряженности электрического поля отлична от нуля. Отметим, что граничное условие Леонтовича-Щукина в предельном случае σ2→∞совпадает с обычным условием Е1τ=0, которое должно выполняться на поверхности идеального проводника.
Так как характеристическое сопротивление в случае хорошо проводящей среды мало, то и касательная составляющая вектора Е на поверхности такой среды будет мала. Однако она определяет нормальную к поверхности проводника компоненту вектора Пойнтинга, т.е. уходящий в металл поток энергии. В инженерных расчетах касательную составляющую вектора Е на поверхности реального проводника обычно не учитывают, кроме тех случаев, когда требуется определить потери в проводнике, т.е. считают, что структура поля над реальным проводником такая же, как и над идеальным проводником той же конфигурации.
Граничное условие (7.52) является приближенным. Это следует непосредственно из его вывода, при котором предполагалось, что образующиеся во второй среде волны распространяются строго по нормали к поверхности раздела. В действительности направление распространения образует некоторый (в случае металлов очень малый) угол с нормалью к поверхности раздела.
Условие (7.52) было получено в предположении, что граница раздела является плоской. При произвольной форме поверхности раздела условием (7.52) можно пользоваться только в тех случаях, если минимальный радиус кривизны поверхности Rminзначительно превышает глубину проникновения Δ0 (см. 6.1.6):

25 . Явление поверхностного эффекта
Выше (см.6.1.5) было показано, что напряженность переменного электрического поля внутри металла, а следовательно, и плотность тока (j = оЕ) экспоненциально убывают по мере удаления от поверхности раздела. На высоких частотах весь ток фактически сосредоточен возле поверхности проводника. Это явление называют поверхностным эффектомили скин-эффектом.
В результате поверхностного эффекта как бы уменьшается сечение провода: эффективное сечение оказывается меньше геометрического. Это приводит к увеличению активного сопротивления провода. На высоких частотах оно может во много раз превысить сопротивление провода при постоянном токе. Кроме того, поверхностный эффект уменьшает магнитную энергию, сосредоточенную внутри проводника, что вызывает уменьшение внутренней индуктивности провода. Очевидно, что поверхностный эффект тем заметнее, чем больше радиус провода. Так как вследствие поверхностного эффекта центральная часть провода, по существу, не используется, то на высоких частотах для экономии металла и уменьшения веса часто сплошные провода заменяют полыми.
Явление поверхностного эффекта позволяет использовать металлические экраны для защиты различных элементов электрических цепей от влияния на них переменного электрического поля. Если экран полностью охватывает объект, а его толщина составляет несколько глубин проникновения (Д°),то внешнее электромагнитное поле практически сквозь него не проникает.
Очевидно также, что при этих условиях существующее внутри экрана поле, в свою очередь, не сможет проникнуть в окружающее пространство. Если защищаемый объект неполностью охватывается экраном, то электромагнитное поле будет частично проникать за экран в результате дифракции волн.
Следует отметить, что в случае постоянных и низкочастотных полей металлический экран не пропускает электрическое поле, но пропускает магнитное, если он выполнен из парамагнитного или диамагнитного металла.
Потери энергии в проводнике
Пусть металлический объект, размеры и минимальный радиус кривизны поверхности которого велики по сравнению с глубиной проникновения, находится в монохроматическом электромагнитном поле. Под воздействием этого поля в металле наводятся электрические токи, на поддержание которых расходуется электромагнитная энергия. Вычислим соответствующую этому процессу среднюю за период мощность джоулевых потерь. Запишем
уравнение баланса средних за период значений мощности для объема V, занимаемого рассматриваемым объектом. Учитывая, что внутри объема V нет сторонних источников, приходим к равенству 0 = Рпср + Рюр,из которого следует, что
 (7.54)
(7.54)
где По-орт внешней нормали к поверхности рассматриваемого объекта S. Как видно, для определения мощности Ргсрнет необходимости вычислять поле внутри объекта, достаточно проинтегрировать по S перпендикулярную к ней составляющую комплексного вектора Пойнтинга. Знак минус в формуле (7.54) объясняется тем, что джоулевы потери определяются потоком энергии, направленным внутрь проводника, а орт п0направлен из объема V в окружающее пространство. Нормальная составляющая вектора
Пойнтинга определяется касательными составляющими векторов
 Испольуя приближенное граничное условие Леонтовича-Щукина, получаем :
Испольуя приближенное граничное условие Леонтовича-Щукина, получаем :

Для сокращения записи введем обоначение 
Раскрывая двойное векторное произведение по формуле получаем

(7.55)
где ц2 и <з2 - абсолютная магнитная проницаемость и удельная проводимость проводника.
Таким образом, средняя за период мощность джоулевых потерь в проводнике

|
Как уже отмечалось, структура поля у поверхности реального проводника близка к структуре поля у такой же поверхности идеального проводника. Поэтому при вычислении потерь обычно предполагают, что H°m = Н° |. Это предположение существенно
упрощает расчеты, обеспечивая достаточную для инженерной практики точность результатов.
Поверхностное сопротивление проводника
Касательная составляющая напряженности электрического поля на поверхности металла Ёч и плотность эквивалентного поверхностного тока js направлены одинаково. Следовательно,
можно записать

Козфффициент пропорциональности Zs принято называть поверхностным сопротивлением проводника. Учитывая формулу (7.50) и граничное условие Леонтовича-Щукина (7.52), получаем, что поверхностное сопротивление

Активная часть поверхностного сопротивления

Из этого выражения следует, что проводник, заполняющий все полупространство, имеет в результате поверхностного эффекта такое же сопротивление, как и слой проводника толщиной Д°без учета поверхностного эффекта (отсюда и термин "глубина проникновения").
Отметим, что среднюю за период мощность потерь в проводнике [формула (7.57)] можно выразить также через эквивалентный поверхностный ток и активную часть поверхностного сопротивления:

26. НАПРАВЛЯЮЩИЕ СИСТЕМЫ ,ВИДЫ НАПРАВЛЯЮЩИХ СИСТЕМ. ВИДЫ Э-М ВОЛН В НАПРАВЛЯЮЩАХ СИСТЕМАХ.
Кроме свободно распространяющихся волн, рассмотренных в предыдущих главах, существуют волны, распространение которых возможно только при наличии каких-либо направляющих элементов (границы раздела сред, металлических, диэлектрических или
пол у проводящих трубок, стержней и др.). Такие волны называют направляемыми. Совокупность направляемых элементов образует направляющую систему. Направляющие системы служат для передачи энергии электромагнитной волны от источника (генератора) к потребителю например от передатчика к антенне, от прием-
ной антенны ко входу приемника и т.д. В связи с этим направляющие системы называют также линиями передачи энергии или, более коротко, линиями передачи. Направляющую систему, у которой поперечное сечение и другие параметры не меняются в продольном направлении, называют однородной. На рис.9.1 изображены поперечнью сечения некоторых используемых на практике однородных направляющих систем: двухпроводной (а), коаксиальной (б), экранированной двухпроводной (в), симметричной (г) и несимметричной (д) полоскоаых линий, диэлектрического волновода (е), световода (ж) и полых металлических волноводов: прямоугольного (з), круглого (и) и эллиптического (к).
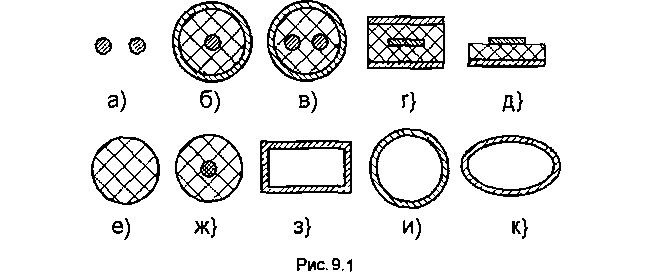
Все линии передачи можно разделить на два класса: линии открытого типа (см., например, рис. 9.1, а, г, д, е, ж) и линии закрытого типа (см., например, pnc.9.1,6,s,3,u,K).В линиях передачи закрытого типа вся передаваемая энергия сосредоточена в области,
экранированной от внешней среды металлической оболочкой той или иной формы. В линиях открытого типа электромагнитное поле, строго говоря, распределено во всем пространстве, окружающем линию. Линии открытого типа обычно выполняют таким образом, чтобы подавляющая часть передаваемой энергии была сосредоточена в непосредственной близости к линии. Тем не менее линии открытого типа подвержены влиянию внешних воздействий. На волны в таких линиях влияют электромагнитные лоля, созданные другими источниками, и внешние условия (например, метеорологические: дождь, снег, обледенение).
По структуре поля направляемые волны делятся на поперечные, электрические, магнитные и гибридные.
Поперечными воинами, или ТЕМ-волнами (Т- первая буква английского слова transvers, что означает поперечный), называют волны, у хоторых векторы Е и Нперпендикулярны направлению распространения волны, т.е. не имеют продольных составляющих.
Отметим, что в соответствии с ГОСТ 18238-72 (Линии передачи сверхвысоких частот. Термины и определения) эти волны полагается называть Г-волнами. Однако это название практически не используется ни в зарубежной, ни в отечественной литературе.
Поэтому в книге сохранен общепринятый термин ТЕIW-волны.
Электрическими волнами, или Е-волнами, называют волны, у которых вектор Еимеет как поперечные, так и продольную составляющие, а продольная состааляющая вектора Нравна нулю. Е-вопны иногда называют поперечными магнитными волнами или Ш-волнами.
Магнитными волнами, или Н-волнами, называют волны, у которых вектор Нимеет как поперечные, так и продольную составляющую, а продольная составляющая вектора Еравна нулю. Н-волны иногда называют поперечными электрическими волнами
или ГЕ-волнами.
Гибридными, или смешанными волнами называют волны, у которых и вектор Е,и вектор Ннаряду с поперечными составляющими имеют и продольные составляющие.
27. Свойства электромагнитных волн различного типа (критическая частота, условие распространения волн, длина направленной волны, фазовая скорость, групповая скорость, дисперсия волн, зависимость волнового сопротивления от частоты). Затухание электромагнитной волны в линиях передачи (причины возникновения затухания)
В случае электрических (Emz≠0, Нтг = 0), магнитных (Hmz≠ 0, Emz= 0) и гибридных (Еmz≠ 0 и Hmz≠0) волн постоянная γ┴ отлична от нуля. Это следует, в частности, из равенств (9.8) и (9.9). Для каждой конкретной линии передачи она может быть определена в результате решения уравнений (9.10) и учета краевых условий, соответствующих этой линии. Постоянная γ┴зависит от формы и размеров поперечного сечения линии передачи и от типа распространяющейся волны, но не зависит от частоты.
Выражая коэффициент фазы β из (9.3), получаем

Так как  то в зависимости от частоты подкоренное
то в зависимости от частоты подкоренное
выражение в (9.11) может быть положительным (при k> γ┴), равным нулю (при k= γ┴) или отрицательным (при k<γ┴).
В первом случае параметр β -действительное число и фазы составляющих векторов поля в фиксированный момент t= to= const линейно зависят от координаты z, что является признаком распространения волны вдоль оси Z с постоянной скоростью vф = ω/β. Как будет видно из дальнейшего, распространение волны в этом случае сопровождается переносом энергии вдоль оси Z.
В третьем случае к< γ┴. Подкоренное выражение в (9.11) оказывается отрицательным, и  Знак в правой части последнего равенства выбран из физических соображений: при этом множитель ехр
Знак в правой части последнего равенства выбран из физических соображений: при этом множитель ехр  и амплитуды составляющих векторов Ёт и Нт экспоненциально убывают вдоль оси
и амплитуды составляющих векторов Ёт и Нт экспоненциально убывают вдоль оси
Z. Если принять β= i | β|, то амплитуды векторов поля будут возрастать с удалением от источников, что в рассматриваемой задаче физически невозможно. Фазы составляющих векторов поля в данном случае не зависят от координат: поле имеет характер стоячей волны и экспоненциально уменьшается вдоль оси Z. Переноса энергии вдоль линии передачи в этом случае не происходит. Подчеркнем, что экспоненциальное убывание поля вдоль линии передачи не связано с потерями энергии: рассматривается идеальная направляющая система, в которой потери отсутствуют.
Во втором случае параметр β = 0. Такой режим называют критическим. Частота f= fкp, определяемая из условия к = γ┴, называется критической частотой:

Соответствующая этой частоте критическая длина волны

Выражая γ┴из (9.13) и подставляя в (9.11), получаем

Как видно, параметр β является действительной величиной, т.е. поле (9.1) представляет собой распространяющуюся волну, только при выполнении условия

Неравенство (9.15) можно переписать в виде

Таким образом, Е-, Н- и гибридные волны в идеальной линии передачи могут распространяться только на частотах, превышающих некоторую критическую частоту, определяемую формулой (9.12). Отметим, что значение fкpзависит от формы и размеров поперечного сечения линии и типа волны.
Неравенство (9.15), а также (9.16) часто называют условием распространения волны в линии передачи.
По аналогии с обычным определением назовем длиной направляемой волны Λ, распространяющейся в линии передачи, расстояние между двумя поперечными сечениями, в которых в один и тот же момент времени фазы составляющих вектора Е(или Н) отличаются на 2π. Очевидно также, что длина волны Λ равна расстоянию, на которое поверхность равной фазы перемещается за период. Так как зависимость всех составляющих векторов поля от координаты zопределяется множителем ехр (- iβz), то

а фазовая скорость вычисляется по формуле

Как видно, при λ< λкрдлина волны в линии и фазовая скорость Е-, Н- и гибридных волн больше соответственно длины волны λ = c/fи фазовой скорости vф=с волны, свободно распространяющейся в безграничной однородной среде без потерь с параметрами ε и μ .
Отметим, что у Е-, Н- и гибридных волн фазовая скорость зависит от частоты. Это явление называют дисперсией волн. При f= fкp(λ = λкр) фазовая скорость равна бесконечности, при увеличении частоты vф приближается к скорости света (рис. 9.2).

Общие выражения для критической длины волны (9.13), критической частоты (9.12), коэффициента фазы (9.14), длины волны в линии (9.17) и фазовой скорости (9.18) одинаковы для Е-, Н- и гибридных волн. Однако из этого не следует, что значения перечисленных параметров будут одинаковыми для этих волн. Критическая длина волны зависит от поперечного волнового числа (λкр= 2π/ γ┴). В свою очередь, значение γ┴ зависит от формы и размеров поперечного сечения линии передачи и от структуры поля распространяющейся волны. Структура поля Е-, Н- и гибридных волн различна, поэтому в общем случае соответствующие данным волнам значения γ┴могут не совпадать. При этом для указанных волн не будут совпадать и значения параметров λкр, frp, β, \/ф и Λ.
Перейдем к вычислению характеристических сопротивлений рассматриваемых волн. По определению характеристическое сопротивление волны равно отношению поперечных к направлению распространения составляющих векторов Ёт и Нт.
В случае Е-волн поперечные составляющие векторов Ёт и Нm определяются формулами

перпендикулярны. Из полученного соотношения вытекает следующее выражение для характеристического сопротивления Е-волн:

Как видно, в случае Н-волн векторы Ёт┴и Нт┴ (и соответствующие им векторы  , как и аналогичные им векторы в случае Е-волн, взаимно перпендикулярны. Характеристическое сопротивление Н-волн зависит от частоты. При λ< λ кроно всегда больше Zc. При увеличении частоты от критической до бесконечности
, как и аналогичные им векторы в случае Е-волн, взаимно перпендикулярны. Характеристическое сопротивление Н-волн зависит от частоты. При λ< λ кроно всегда больше Zc. При увеличении частоты от критической до бесконечности  убывает от бесконечности доZc (см. рис. 9.3).
убывает от бесконечности доZc (см. рис. 9.3).

В области волн длиннее критической (λ > λкР) характеристические сопротивления Е- и Н-волн являются чисто мнимыми величинами. Это означает, что при λ>λкрпоперечные составляющие векторов напряженностей электрического и магнитного полей Ёт┴и Нт┴сдвинуты по фазе на 90°. Очевидно, что при этом комплексный вектор Пойнтинга принимает чисто мнимые значения, т.е. вдоль линии не происходит переноса энергии. Поле в линии при λ > λкР является чисто реактивным. Напомним, что все формулы данного раздела получены в предположении, что линия является идеальной (не вносит потерь).
В случае гибридных волн (Emz≠0 и Нmz # 0) поперечные составляющие векторов Ёт и Нтопределяются общими формулами (9.8) и (9.9). Поэтому получить единое простое выражение для характеристического сопротивления не удается: его величина зависит и от линии передачи, и от структуры поля распространяющейся волны и при λ < λкР может быть как больше, так и меньше Zc. На частотах, меньших критической (λ > λкР), характеристическое сопротивление гибридных волн также принимает чисто мнимые значения.
Свойства TEM - волн
Так как в случае ТЕМ-волн γ┴= 0, то коэффициент фазы, фазовая скорость и длина волны будут совпадать с аналогичными параметрами волны, свободно распространяющейся в безграничной однородной изотропной среде:

Характеристическое сопротивление ТЕМ-волны легко находится из уравнений (9.4). Полагая в этих уравнениях Еmz = 0 и Hmz= 0, приходим к соотношениям, которые можно записать в виде векторного равенства

Как видно, ZCTEMсовпадает с характеристическим сопротивлением волны, свободно распространяющейся в безграничной однородной среде с параметрами εи μ.
Отметим, что равенства (9.22), (9.25) и (9.30) однотипны и отличаются только значениями характеристических сопротивлений. Эти равенства можно объединить в одну формулу:

Поле, удовлетворяющее таким уравнениям, является потенциальным. Это означает, что решения уравнений (9.33) могут быть представлены в виде градиентов от некоторых скалярных функций, например:
E0=-gradu0, (9.34)
где функция и° зависит только от поперечных координат и удовлетворяет уравнению Лапласа ∆┴2u°=0. Аналогичное представление для вектора Й°т┴можно не выписывать, так как векторы Ё°и Н°связаны соотношением, аналогичным (9.30): H°=(1/Zc)x
x[zo,E°].
В уравнения (9.33) не входит частота. Из этого следует, что функции Ё° и Н°, определяющие структуру поля в поперечных сечениях линии, не зависят от частоты и могут быть найдены на основе решения рассматриваемой задачи при f→0. Для определения вектора Ё° достаточно решить двумерную электростатическую задачу для такой же линии. При этом во многих случаях целесообразно вначале определить функцию и0, которую можно трактовать как электростатический потенциал указанной электростатической задачи, а затем воспользоваться формулой (9.34).
Функция Н° совпадает с напряженностью магнитного поля, создаваемого постоянными токами, текущими по рассматриваемой линии при f→0. Поэтому она может быть найдена либо непосредственно, если известно распределение токов, либо по
формуле, аналогичной (9.30), после определения вектора Ё°.
|
Просмотров 1151 |
|
|
