
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

ІІІ. Умови невід’ємності змінних
|
|
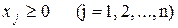
На базі наведеного математичного опису можна проілюструвати суть цієї моделі так: необхідно визначити значення n невід’ємних змінних  , які задовольняють обмеженням 2.2та забезпечують екстремальне значення (максимальне або мінімальне) цільової функції, яка виражена рівнянням 2.1.
, які задовольняють обмеженням 2.2та забезпечують екстремальне значення (максимальне або мінімальне) цільової функції, яка виражена рівнянням 2.1.
До методів вирішення задач ЛП відносяться симплекс-метод, графічний метод.
Симплекс-метод є аналітичним методом знаходження рішення задач ЛП.
Як правило, задачу зводять до канонічної форми. Вважають, що задача лінійного програмування записана в канонічній формі, якщо вона має вигляд
 (2.3)
(2.3)
Щоб перевести задачу лінійного програмування з загальної форми (2.1–2.2) до канонічної форми (2.3) необхідно зробити такі кроки.
1-й крок.До кожної лівої частини нерівностей (2.2) додаємо нову невід'ємну невідому змінну хп+і (i= 1,2,...,l–k), яка дорівнює:

або:

Тоді група нерівностей(2.2)перетвориться на рівняння.
Введені нові змінні, хп+і, ... , хт–k будемо вважати базовими, а змінні
x1, ... , хп – вільними.
Дістаємо однорідну систему основних обмежень задачі:

2-й крокполягає у зведенні до однорідної системи обмежень на знак. Умови недодатності легко перетворюються в умови невід'ємності за допомогою заміни змінних

Змінну, на знак якої не накладено обмежень, подають у вигляді різниці двох невід'ємних змінних:

Ранг сумісної системи обмежень (1.3) r можна вважати таким, що дорівнює т, оскільки в іншому разі частину, а саме т – r = k рівнянь треба було б відкинути, бо вони були б лінійними комбінаціями r базових рівнянь. Однак на практиці інколи такі зайві рівняння можуть включати в систему обмежень на стадії формування реальної задачі. Такі обмеження називають неістотними і їх відкидають, що звичайно відбувається при побудові довільного базового розв'язку системи рівнянь. Отже, знайти множину планів задачі – означає знайти множину невід'ємних розв'язків системи лінійних рівнянь.
Означення. Задачу лінійного програмування вважають записаною у канонічній формі, якщо вона задовольняє такі умови:
1. Система обмежень зведена до системи рівнянь виду (2.3).
2. Система рівнянь зображена в такому вигляді, де кожна базова невідома входить тільки в одне рівняння системи з коефіцієнтом рівним одиниці, при чому немає рівнянь, в які не входила хоча б одна базова невідома. Якщо деякі рівняння системи поміняти місцями так, щоб нумерація базових невідомих була строго зростаючою, то базовий мінор в цьому випадку складає одиничну матрицю.
3. Вільні члени системи обмежень невід'ємні;
4. Оптимізуюча форма залежить тільки від вільних невідомих.
Отже, для того, щоб задачу лінійного програмування можна було розв'язувати симплексним методом потрібно загальну форму(2.1–2.2)звести до канонічної форми. Іншими словами її потрібно певним способом записати в такій формі, щоб система рівнянь була з базисом.
 (2.4)
(2.4)
 (2.5)
(2.5)
Для того, щоби базовий план системи обмежень (2.4)був опорним, необхідно і достатньо, щоб всі вільні члени (2.5) були невід'ємні. Отже, для зведення задачі до канонічної форми потрібно так підібрати базові невідомі, щоб у загальному розв'язку системи обмежень не було від'ємних вільних членів.
Приклад.
Для виготовлення двох видів продукції А і В використовують три види сировини: I, II та III.
На виробництво одинці продукції А знадобиться витратити:
сировини I виду – 15 кг,
сировини II виду – 12 кг,
сировини III виду – 3 кг.
На виробництво одинці продукції В знадобиться витратити:
сировини I виду – 2 кг,
сировини II виду – 6 кг,
сировини III виду – 12 кг.
Запаси сировини:
I виду – 300 кг,
II виду – 306 кг,
III виду – 360 кг
Прибуток від реалізації одиниці продукції виду А становить 9 грн.,
виду В– 6 грн.
Скласти план виробництва продукції, який забезпечить максимальний прибуток від реалізації при наявності даних запасів сировини.
Розв'язування
Позначимо кількість виготовленої продукції першого виду Ачерез х1, другого – х2. Враховуючи витрати сировини I, II та III виду на виготовлення одиниці продукції видів АтаВ, а також обмежені запаси сировини, запишемо систему обмежень (6.1). Прибуток, одержаний з виготовлення продукції у вигляді функції мети (6.2).
 (2.6)
(2.6)
 (2.7)
(2.7)
Зведемо задачу лінійного програмування (2.6, 2.7) до канонічної форми додавши невідомі х3, х4 та х5 до лівої сторони двох нерівностей відповідно:
 (2.8)
(2.8)
 ;
;
 .
.
Розв'яжемо систему рівнянь методом Гаусса-Джордана, тому запишемо систему обмежень (2.8) у вигляді початкової розрахункової таблиці, яку назвемо ітерацією 1.
Для знаходження початкового базового плану розділимо змінні на дві групи – базові і вільні. Для вибору базових змінних доцільно скористатися таким правилом: в якості базових змінних ітерації симплекс-таблиці необхідно вибрати такі змінні (їх кількість визначається числом основних обмежень), кожна з яких тільки раз входить у рівняння основних обмежень. Решту змінних будемо вважати вільними.
Запишемо цільову форму f у вигляді рівняння

Таблиця заповнюється формально за вибраною канонічною формою.
1. Заповнюємо базові стовпчики: на перетині однойменних рядків і стовпчиків ставимо 1, а в усіх інших клітинках будуть нулі.
2. В інших рядках виписуємо коефіцієнти, що стоять біля відповідних невідомих. Нульовий рядок відповідає оптимізуючій формі і служить для визначення ступеня оптимальності опорного плану.

Ітерація 1
| f 0 | –9 | –6 | |||||
| Базові невідомі | № рядка | План (опорний розв'язок) | x1 | x2 | x3 | x4 | x5 |
| x3 | 15 | ||||||
| x4 | |||||||
| x5 |
Критерій оптимальності. Якщо задача максимізується і в нульовому рядку відсутні від'ємні числа (за винятком хіба що стовпчика "опорний розв'язок (план)"), то опорний план є оптимальним (при мінімізації задачі для оптимальності плану достатньо відсутності додатних чисел у нульовому рядку, за винятком, можливо, опорного розв'язку).
Коефіцієнт рядка "0" можна інтерпретувати як приріст функції f при збільшенні вільної невідомої на одиницю. Приріст буде додатним, якщо коефіцієнт від'ємний, і від'ємним – якщо коефіцієнт додатний.
В нашому випадку є два від'ємні числа (–9), (–6), беремо найбільше за модулем від'ємне число (–9) (при мінімізації задачі – найбільше додатне), тоді стовпчик "х1"будемо називати ключовим стовпчиком.
Для вибору ключового елемента складаємо відношення вільних членів (чисел стовпчика "опорний розв'язок") до відповідних додатних чисел ключового стовпчика (усі інші відношення будемо вважати рівними нескінченності):
 .
.
Перше відношення менше, тому число (15) першого рядка буде ключовим елементом. Ключовий елемент в таблиці позначаємо рамкою і переходимо до другої ітерації.
Ітерація 2
| f 0 | 
| 
| |||||
| Базові невідомі | № рядка | План (опорний розв'язок) | x1 | x2 | x3 | x4 | x5 |
| х1 | 
| 
| |||||
| x4 | 
| 
| |||||
| x5 | 
| 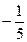
|
Послідовність заповнення другої та наступних ітерацій така (використовуємо метод Гаусса-Жордана):
1. Замість базової невідомої х3 (ключовий рядок), вводимо
нову базову невідому х1 (невідому ключового стовпчика),
2. Формально заповнюємо базові стовпчики (пункт 1 ітерації 1).
3. Ключовий рядок одержуємо від ділення його елементів
попередньої ітерації на ключовий елемент.
4. Усі інші комірки ітерації заповнюємо за правилом прямокутника:

 (2.9)
(2.9)
де aij', bi ' відповідно шукані елементи нової ітерації, а аij, bi – попередньої,
аqs – ключовий елемент.
Рядок 0:  ;
; 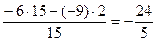 ;
;  .
.
Рядок 2:  ;
;  ;
;  ;
;  .
.
Рядок 3:  ;
;  ;
;  ;
;
 .
.
Після заповнення таблиці 2-ої ітерації перевіряємо її опорний план на оптимальність. Бачимо, що потрібно перейти до наступного опорного плану, оскільки в нульовому рядку стовпчика "х2" знаходиться від'ємне число (  ).
).
 .
.
За ключовий елемент слід взяти число "  ".
".
Ітерація 3
| f 0 | 
| 
| |||||
| Базові невідомі | № рядка | План (опорний розв'язок) | x1 | x2 | x3 | x4 | x5 |
| х1 | 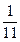
| 
| |||||
| х2 | 
| 
| |||||
| x5 | 
| 
|
В ітерації 3 замість базової змінної х4 тепер буде нова базова х2, ключовим буде рядок 2. Над таблицею виконуємо ті ж операції, що й під час другої ітерації.
Після III-ої ітерації перевіряємо опорний план на оптимальність. Бачимо, що потрібно перейти до наступного опорного плану, оскільки в нульовому рядку стовпчика "х3" знаходиться від'ємне число (  ).
).
 .
.
За ключовий елемент слід взяти число "  ".
".
Ітерація 4
| f 0 | 
| 
| |||||
| Базові невідомі | № рядка | План (опорний розв'язок) | x1 | x2 | x3 | x4 | x5 |
| х1 | 
| 
| |||||
| х2 | 
| 
| |||||
| х3 | 
| 
|
В рядку 0 вже немає від'ємних чисел, тому опорний план останньої таблиці оптимальний і виписуємо його із стовпчика "опорний розв'язок"





 .
.
*Зауваження 1. Кожній таблиці відповідає своя канонічна форма стандартного запису. Так, наприклад, за останньою таблицею можна записати таку канонічну форму:


*Зауваження 2. Контролювати правильність обчислення опорних планів і оптимального значення можна за значенням функції мети:

*Зауваження 3. При розв'язуванні задачі для зручності ітерації послідовно записують одну під одною.
|
Просмотров 500 |
|
|
