Диференціальні рівняння першого порядку

Конспект лекцій з вищої математики

Р о з д і л : „Диференціальні рівняння”

Звичайні диференціальні рівняння

Основні означення

Різноманітні геометричні, фізичні, технічні та іншого характеру задачі часто приводять до рівнянь, які крім незалежних змінних і невідомих функцій містять ще й похідні цих функцій.

Означення.Нетотожне співвідношення між змінними та їх похідними (або диференціалами) зветься диференціальним рівнянням.

Якщо шукана функція залежить від одного аргументу, то диференціальне рівняння зветься звичайним. Лише такі рівняння і будемо вивчати у першому розділі.

Символічно звичайне диференціальне рівняння можна записати у вигляді

(1)

В (1) х − незалежна змінна, 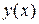− шукана функція, − звичайні похідні від функції 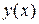першого, другого і п-го порядку відповідно.

Порядок найвищої похідної, яку містить дане диференціальне рівняння, звуть порядкомцього рівняння.

Отже,

є звичайне диференціальне рівняння першого порядку, а

є теж звичайне диференціальне рівняння, але другого порядку.

Означення. Розв’язком диференціального рівняння(1) зветься кожна функція , яка, будучи підставлена в рівняння, перетворює його на тотожність.

Процес відшукання таких функцій зветься інтегруванням диференціальних рівнянь.

Диференціальні рівняння першого порядку

Загальний вигляд диференціального рівняння першого порядку

Якщо його розв’язати відносно , то воно матиме вигляд

(2)

Тільки такі рівняння, тобто рівняння у вигляді (2), ми і будемо вивчати у цьому підрозділі.

Приклад 1.Показати, що функція є розв’язком диференціального рівняння

(3)

Справді, , отже підставлення функції дає тотожність

Легко перевірити також, що функція , де С − довільна стала, також є розв’язком рівняння (3). Цей розв’язок називається загальним розв’язкомрівняння (3). При С = 0 з нього можна отримати розв’язок 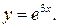Більше того, залежно від значення С ми отримуємо з загального розв’язку цілий набір частинних розв’язків.

Задаючи, наприклад, таку початкову умову

, (4 )

де і 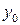− задані числа, можна отримати будь-який частинний розв’язок диференціального рівняння (3). Для цього знайдемо довільну сталу С у загальному розв’язку :

У результаті отримуємо частинний розв’язок рівняння (3)

який задовольняє умову (4).

Знайти єдиний розв’язок рівняння (2), який задовольняє початкову умову (4), − це одна з найважливіших задач теорії диференціальних рівнянь. Ця задача називається задачею Коші. Доведено, що задача (2), (4) має єдиний розв’язок, коли функція неперервна в області розв’язання задачі і має обмежену похідну в цій області (теорема Коші).

Функцію завжди можна подати у вигляді частки двох відомих функцій

і записати рівняння (2) у такий спосіб

або

Ця форма запису дає співвідношення між змінними х, у та їх диференціалами. Вона зручна тим, що тут х та у рівноправні, тобто кожну з них можна розглядати як функцію другої.

Далі розглянемо деякі типи рівнянь першого порядку і для кожного з них викладемо притаманні способи їх інтегрування.