Лінійні диференціальні рівняння першого порядку

Диференціальне рівняння першого порядку звуть лінійним, якщо шукана функція та її похідна входять у рівняння у першому степені (лінійно) і не перемножуються. Лінійне рівняння має вигляд

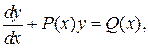(9)

де і − дані неперервні функції від х, або сталі величини. Коли , то рівняння

(10)

зветься лінійним однорідним рівнянням. У зв’язку з цим рівняння (9) звуть лінійним неоднорідним рівнянням. Лінійне однорідне рівняння (10), ліва частина якого ідентична з лівою частиною неоднорідного рівняння (9), звуть відповідним цьому неоднорідному рівнянню.

У рівнянні (10) змінні відокремлюються і його легко зінтегрувати. Маємо

Звідси

або

(11)

Це загальний розв’язок лінійного однорідного рівняння (10). В ньому С − довільна стала. Для відшукання загального розв’язку лінійного неоднорідного рівняння (9) існує кілька способів. Викладемо один з них.

Спосіб варіації довільної сталої. Інтегруємо спочатку відповідне лінійне однорідне рівняння (10). Дістанемо його розв’язок у вигляді

(11)

Розглядаючи далі у цьому розв’язку С як функцію від х, тобто , спробуємо підібрати функцію так, щоб функція

(12)

була розв’язком неоднорідного рівняння (9). По суті цим самим робиться заміна змінної, де - нова невідома функція.

Обчислимо похідну функції (12). Маємо

.

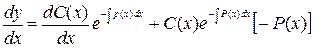Підставлення у рівняння (9) дає

,

або, після скорочення,

.

Звідси, інтегруючи, знаходимо невідому функцію

.

Отже,

є шуканий загальний розв’язок лінійного неоднорідного рівняння (9).

Приклад 5.Зінтегрувати рівняння

.

Це рівняння є лінійне 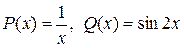. Перепишемо його, враховуючи, що . Отримаємо

. (13)

На першому етапі розв’язання шукаємо розв’язок відповідного однорідного рівняння

. (14)

Відокремлюючи у ньому змінні, матимемо

.

Інтегруючи останнє рівняння почленно, знайдемо загальний розв’язок диференціального рівняння (14):

, де .

Потенціювання останньої рівності дає , або , де С – нова довільна стала. З загального інтегралу рівняння (14) отримаємо нарешті загальний розв’язок цього рівняння у вигляді

(15)

На другому етапі розв’язання шукаємо загальний розв’язок лінійного неоднорідного рівняння (13) у вигляді

, (16)

замінюючи довільну сталу С розв’язку (15) відповідного однорідного рівняння (14) на функцію .

Для знаходження функції підставимо (16) у рівняння (13). Матимемо

,

або, після скорочень,

,

звідки

.

Почленне інтегрування останнього рівняння дозволяє отримати :

Підставлення одержаного виразу для у (16) дозволяє отримати загальний розв’язок лінійного неоднорідного рівняння (13)

.

Приклад 6. Зінтегрувати рівняння

. (17)

Знайти також частинний розв’язок при . Це рівняння теж лінійне .

Шукаємо розв’язок відповідного однорідного рівняння

. (18)

Маємо

.

Покладаючи в одержаному загальному інтегралі рівняння (18) , де - нова довільна стала, отримаємо

. (19)

Такий вигляд загального інтегралу рівняння (18) дозволяє знайти у, як явну функцію х. Після потенціювання у (19) матимемо

, (20)

де С – нова довільна стала.

На другому етапі розв’язання шукаємо загальний розв’язок лінійного неоднорідного рівняння (17) у вигляді

, (21)

замінюючи сталу С розв’язку (20) на функцію .

Для знаходження функції підставимо (21) у рівняння (17)

.

Після очевидних скорочень отримаємо

.

Звідки і . Отже, загальний розв’язок рівняння (17) буде

.

Щоб знайти потрібний частинний розв’язок, покладемо , тоді , отже, і шуканий частинний розв’язок рівняння (17) буде

.