Багатовимірні випадкові величини

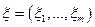Випадкові вектори, їх розподіли. Нехай на ймовірнісному просторі задані випадкові величини . Вектор - називається -вимірним випадковим вектором або -вимірною випадковою величиною.

.

Ймовірність називають розподілом випадкового вектора .У частинному випадку, якщо , одержимо функцію, яку називають функцією розподілу випадкового вектора :

.

Подія розглядається як сумісне настання подій ,…, .

Очевидно,

.

,

.

Із останньої властивості випливає, що за функцією розподілу вектора можна знайти функцію розподілу вектора для довільного k=1,…,m, зокрема, можна знайти функцію розподілу кожної компоненти вектора.

Відзначимо також, що функція розподілу по кожній із змінних неспадна і неперервна зліва.

Розглянемо двовимірний випадковий вектор . Тоді для функції розподілу будуть справедливі рівності:

,

, ,

.

Якщо існує функція така, що

,

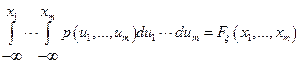то функцію 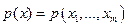називають щільністю розподілу випадкового вектора , а розподіл випадкового вектора називають абсолютно неперервним.

Із даного означення випливає:

1) ;

2) якщо – точка неперервності , то ;

3) ;

4) для довільної борелєвої множини

.

Знаючи щільність розподілу випадкового вектора, можна знайти щільності розподілу його компонент. Розглянемо, як частинний випадок, двовимірну випадкову величину зі щільністю . Тоді

,

звідки

,

а

.

Випадковий вектор називається дискретним, якщо множина його значень скінченна або зліченна. Розглянемо для спрощення двовимірну випадкову величину . Нехай 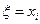, , , , тоді кожній парі можна поставити у відповідність ймовірність . Тут . Таку відповідність називають законом розподілу. Його можна подати у вигляді такої таблиці:

		.....
		.....
…	…	.....	…..	…..
		.....
		.....

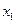
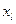
Якщо , то утворюють повну групу і , тому . Отже, за аксіомою адитивності . Так само . При цьому, .

Деякі розподіли функцій від нормально розподілених випадкових величин. Нехай випадкові величини – незалежні, . Тоді випадкова величина має розподіл Пірсона (або розподіл ) із ступенями вільності.

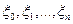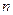Нехай – незалежні нормально розподілені з параметрами випадкові величини. Тоді величина має розподіл Стьюдента (або -розподіл) із ступенями вільності.

Нехай , – незалежні нормально розподілені з параметрами випадкові величини, . Тоді величина має розподіл Фішераіз ступенями вільності.

Нормальний розподіл, розподіли Пірсона, Стьюдента, Фішера мають дуже широке використання у математичній статистиці.

Числові характеристики випадкових величин

Математичне сподівання

Означення математичного сподівання. Приклади. Нехай випадкова величина – дискретна із можливими значеннями і відповідними ймовірностями . Сума добутків можливих значень випадкової величини на ймовірності, з якими ці значення приймаються, називається математичнимсподіваннямдискретної випадкової величини (якщо множина значень випадкової величини зліченна, то за умови збіжності ряду 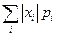) і позначається або :

. (1)

Нехай випадкова величина – неперервна із щільністю , тоді

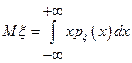, (2)

якщо інтеграл – збіжний.

Часто математичне сподівання називають середнім значенням випадкової величини. Для математичного сподівання використовують і таке позначення: .

Приклади.