
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Інтервальні оцінки невідомих параметрів розподілу
|
|
Поняття довірчого інтервалу. Довірчий інтервал для невідомої ймовірності у схемі Бернуллі. При реалізації вибірки в кожному конкретному випадку значення оцінки може відрізнятись від оцінюваного параметра, тому необхідно знати похибку, яку ми допускаємо при заміні невідомого параметра його оцінкою. Тобто, в багатьох випадках важливо знати не тільки оцінку невідомого параметра  , але знати і область
, але знати і область  , що містить в собі значення параметра
, що містить в собі значення параметра  . Така область будується за статистичними даними і змінюється від вибірки до вибірки, тому є випадковою. Отже можна говорити про ймовірність того, що дана область містить невідомий параметр. Якщо існує область
. Така область будується за статистичними даними і змінюється від вибірки до вибірки, тому є випадковою. Отже можна говорити про ймовірність того, що дана область містить невідомий параметр. Якщо існує область  , яка з ймовірністю, що не менше
, яка з ймовірністю, що не менше  , містить невідомий параметр
, містить невідомий параметр  , то область
, то область  називають довірчою областю, а число
називають довірчою областю, а число  називають надійністю (і воно має бути близьким до одиниці). Якщо параметр
називають надійністю (і воно має бути близьким до одиниці). Якщо параметр  одновимірний, то для параметра
одновимірний, то для параметра  знаходять довірчий інтервал, який задається двома статистичними оцінками, що є кінцями інтервалу. В цьому випадку говорять про інтервальне оцінювання.
знаходять довірчий інтервал, який задається двома статистичними оцінками, що є кінцями інтервалу. В цьому випадку говорять про інтервальне оцінювання.
Розглянемо дві оцінки  і
і  невідомого параметра
невідомого параметра  і розглянемо інтервал
і розглянемо інтервал  , де
, де  . Нехай
. Нехай  , тобто
, тобто  , тоді
, тоді  називається надійністюоцінки, а інтервал
називається надійністюоцінки, а інтервал  – надійнимабо довірчимінтервалом, який з надійністю
– надійнимабо довірчимінтервалом, який з надійністю  оцінює невідомий параметр
оцінює невідомий параметр  (
(  -довірчим інтервалом).
-довірчим інтервалом).
Для забезпечення однозначності визначення довірчого інтервалу  , межі інтервалу
, межі інтервалу  і
і  вибирають так, щоб виконувались умови
вибирають так, щоб виконувались умови 
 .
.
Якщо  , то в цьому випадку
, то в цьому випадку  називається точністю оцінки. Виберемо
називається точністю оцінки. Виберемо  так, щоб
так, щоб  . Тоді інтервал
. Тоді інтервал

буде довірчим інтервалом, який із надійністю  оцінює невідомий параметр
оцінює невідомий параметр  . Точність оцінки
. Точність оцінки  залежить від надійності
залежить від надійності  і обсягу вибірки
і обсягу вибірки 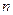 .
.
Розглянемо один із методів знаходження інтервальних оцінок за допомогою емпіричної функції розподілу. Нехай досліджувана величина  має функцію розподілу
має функцію розподілу  і існує
і існує  . Покладемо
. Покладемо
 .
.
Тоді оцінка (5)


є незміщеною і сильно спроможною оцінкою параметра  . Із (7) випливає, що величина
. Із (7) випливає, що величина
 ,
,
де 
 , асимптотично нормальна (0,1). Тому
, асимптотично нормальна (0,1). Тому
 ,
,
де  – функція Лапласа.
– функція Лапласа.
По надійності  можна знайти таке число
можна знайти таке число  , щоб
, щоб  . Тоді при великих
. Тоді при великих 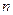 приблизно з ймовірністю
приблизно з ймовірністю  буде виконуватись нерівність
буде виконуватись нерівність  або
або
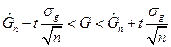 . (12)
. (12)
Побудована інтервальна оцінка параметра  є незручною, бо містить величину
є незручною, бо містить величину  , яка може бути невідомою. Але при великих
, яка може бути невідомою. Але при великих 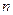
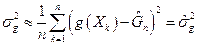 .
.
Замінимо в (12)  на
на  . Тоді знову при великих
. Тоді знову при великих 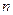 приблизно з ймовірністю
приблизно з ймовірністю  буде виконуватись нерівність
буде виконуватись нерівність
 . (13)
. (13)
Подібний метод ми уже використовували при оцінці ймовірності в схемі Бернуллі (розділ 2). Знайдемо тепер довірчий інтервал для невідомої ймовірності  у схемі Бернуллі. Із теореми Бореля випливає, що оцінка
у схемі Бернуллі. Із теореми Бореля випливає, що оцінка  (відносна частота події
(відносна частота події  , а
, а  , де
, де  – число появ події в
– число появ події в  му експерименті) є сильно спроможною і незміщеною оцінкою параметра
му експерименті) є сильно спроможною і незміщеною оцінкою параметра  . Оскільки
. Оскільки  , а
, а  , то величина
, то величина  за ценральною граничною теоремою при великих
за ценральною граничною теоремою при великих 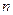 має розподіл близький до стандартного нормального закону, тобто
має розподіл близький до стандартного нормального закону, тобто  . Задамо надійність
. Задамо надійність  близьку до 1 і знайдемо
близьку до 1 і знайдемо  із рівняння
із рівняння  . Тоді при великих
. Тоді при великих 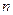 із надійністю, що близька до
із надійністю, що близька до  , виконується нерівність
, виконується нерівність 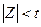 або
або
 . (14)
. (14)
Якщо розв’яжемо нерівність (14) відносно  , то одержимо
, то одержимо
 .
.
Якщо, аналогічно переходу від (12) до (13), у лівій і правій частинах нерівності (14)  замінити на
замінити на  , то одержимо більш простий вигляд довірчого інтервалу для невідомої ймовірності:
, то одержимо більш простий вигляд довірчого інтервалу для невідомої ймовірності:
 . (15)
. (15)
Якщо врахувати, що  , то із ймовірністю, що близька до
, то із ймовірністю, що близька до  , при великих
, при великих 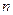 виконується нерівність
виконується нерівність
 .
.
Але остання оцінка є досить грубою. Частіше використовують інтервал у вигляді (15). У цьому інтервалі величина  є точність оцінки невідомої ймовірності із надійністю
є точність оцінки невідомої ймовірності із надійністю  .
.
Довірчі інтервали для параметрів нормального розподілу. Щільність нормального розподілу з параметрами  і
і  має вигляд:
має вигляд:  , де
, де 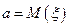 ,
,  .
.
Розглянемо окремі випадки знаходження довірчих інтервалів для параметрів  і
і  . Для цього використаємо наступну теорему, яку ми приймемо без доведення.
. Для цього використаємо наступну теорему, яку ми приймемо без доведення.
Теорема. Нехай випадкові величини 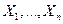 – незалежні і нормально розподілені з параметрами
– незалежні і нормально розподілені з параметрами  . Тоді вибіркова середня
. Тоді вибіркова середня 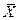 і вибіркова дисперсія
і вибіркова дисперсія  незалежні і величини
незалежні і величини  мають розподіл
мають розподіл  з (
з (  ) ступенями вільності.
) ступенями вільності.
а) Знайдемо довірчі інтервали для невідомого метематичного сподівання 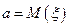 , коли
, коли  – відоме. За оцінку невідомого математичного сподівання виберемо
– відоме. За оцінку невідомого математичного сподівання виберемо  . Оскільки
. Оскільки  , де
, де  – нормально розподілені випадкові величини, то
– нормально розподілені випадкові величини, то  є також номально розподіленою величиною із параметрами
є також номально розподіленою величиною із параметрами  і
і  . Тому величина
. Тому величина  буде мати стандартний нормальний розподіл і
буде мати стандартний нормальний розподіл і 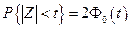 . За надійністю
. За надійністю  можна знайти
можна знайти  як розв’язок рівняння
як розв’язок рівняння  . Тоді із надійністю
. Тоді із надійністю  буде виконуватись нерівність
буде виконуватись нерівність  або
або
 ,
,
де величина

є точністю оцінки.
Тобто, довірчий інтервал, який із надійністю  оцінює невідоме метематичне сподівання
оцінює невідоме метематичне сподівання 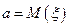 , коли
, коли  – відоме, має вигляд
– відоме, має вигляд
 ,
,
де число  знаходиться із рівняння
знаходиться із рівняння  .
.
б) Нехай  – невідоме. Величина
– невідоме. Величина  є незміщеною і спроможною оцінкою для
є незміщеною і спроможною оцінкою для  . Тоді величина
. Тоді величина  має стандартний нормальний розподіл, а за наведеною теоремою, величина
має стандартний нормальний розподіл, а за наведеною теоремою, величина  буде мати розподіл
буде мати розподіл  із
із  ступенями вільності, при цьому, ці величини є незалежними. Тому величина
ступенями вільності, при цьому, ці величини є незалежними. Тому величина  буде мати розподіл Стьюдента із
буде мати розподіл Стьюдента із  ступенями вільності (
ступенями вільності (  – виправлене середнє квадратичне відхилення).
– виправлене середнє квадратичне відхилення).
Якщо надійність  задана, то за розподілом Стьюдента можна знайти таке число
задана, то за розподілом Стьюдента можна знайти таке число  , яке задовольняє умову
, яке задовольняє умову  . Тоді із надійністю
. Тоді із надійністю  буде виконуватись нерівність
буде виконуватись нерівність  або
або
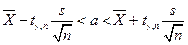 ,
,
де

– точність оцінки.
Тобто, довірчий інтервал, який із надійністю  оцінює невідоме метематичне сподівання
оцінює невідоме метематичне сподівання 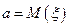 , коли
, коли  – невідоме, має вигляд
– невідоме, має вигляд
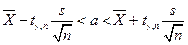 ,
,
де число  знаходиться за надійністю
знаходиться за надійністю  і числом ступенів вільності (
і числом ступенів вільності (  ) за розподілом Стьюдента із умови
) за розподілом Стьюдента із умови  .
.
в) Довірчі інтервали для невідомої дисперсії  . Якщо
. Якщо  відоме, то оцінкою дисперсії є величина
відоме, то оцінкою дисперсії є величина  . Оскільки величини
. Оскільки величини  мають стандартний нормальний розподіл, то величина
мають стандартний нормальний розподіл, то величина  має розподіл
має розподіл  з
з 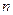 ступенями вільності (
ступенями вільності (  ). При заданій надійності
). При заданій надійності  за розподілом
за розподілом  можна знайти такі числа
можна знайти такі числа  і
і  , щоб виконувались умови
, щоб виконувались умови  і
і  . Тоді із надійністю
. Тоді із надійністю  буде виконуватись нерівність
буде виконуватись нерівність 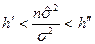 або
або  .
.
Отже, довірчий інтервал, який із надійністю  оцінює невідому дисперсію
оцінює невідому дисперсію  , коли
, коли  – відоме, має вигляд
– відоме, має вигляд
 ,
,
де числа  і
і  вибираються так, щоб виконувались умови
вибираються так, щоб виконувались умови  і
і  .
.
Нехай  – невідоме. Тоді величина
– невідоме. Тоді величина  є оцінкою для
є оцінкою для  . За теоремою (стор. 150), величина
. За теоремою (стор. 150), величина  має розподіл
має розподіл  . При заданій надійності
. При заданій надійності  за розподілом
за розподілом  можна знайти такі числа
можна знайти такі числа  і
і  , щоб виконувались умови
, щоб виконувались умови  і
і  . Тоді із надійністю
. Тоді із надійністю  буде виконуватись нерівність
буде виконуватись нерівність  або
або  .
.
Отже, довірчий інтервал, який із надійністю  оцінює невідому дисперсію
оцінює невідому дисперсію  , коли
, коли  – невідоме, має вигляд
– невідоме, має вигляд
 ,
,
де числа  і
і  вибираються так, щоб виконувались умови
вибираються так, щоб виконувались умови  і
і  .
.
|
Просмотров 1916 |
|
|
