Перевірка статистичних гіпотез

Поняття статистичної гіпотези і статистичного критерію. Критерій Неймана-Пірсона. Однією із важливіших задач математичної статистики є задача перевірки статистичних гіпотез на основі статистичних даних, перевірка відповідності результатів експериментів сформульованій гіпотезі. Статистичною гіпотезою (або просто гіпотезою) називають будь-яке твердження про вигляд або властивості розподілу досліджуваних в експерименті випадкових величин. Тобто гіпотези, у яких іде мова про невідомий розподіл або невідомі параметри розподілу, є статистичними. Наприклад, твердження, досліджувана величина має нормальний розподіл, є статистичною гіпотезою. Часто розподіл досліджуваної величини відомий, а необхідно перевірити гіпотези про значення параметрів цього розподілу. Такі гіпотези називають параметричними.

Висунуту гіпотезу, яка має піддаватися перевірці, позначають 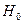і називають основноюабо нульовою гіпотезою. Поряд із основною розглядають гіпотезу, що протирічить основній, її називають альтернативною (альтернативою до гіпотези 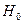) або конкурентною. Наприклад, нехай , . Гіпотеза буде альтернативною, якщо . Якщо при цьому множина точок складається лише із одного елемента, то гіпотеза називається простою. Тобто гіпотеза є простою, якщо їй відповідає один розподіл або одна точка в просторі параметрів, в іншому разі – складною.

Статистичні гіпотези перевіряються на основі статистичних даних. Для перевірки статистичних гіпотез вибирається деяка випадкова величина, яка залежить від результатів спостережень, тобто є статистикою. Статистики, які вибирають для перевірки гіпотез, називають статистиками критерію або критеріями. Нехай вибраний деякий критерій .

Множину значень критерію розбивають на дві області: область прийняття гіпотези – множина значень критерію, при яких гіпотеза приймається; критичну область S – множина значень критерію, при яких гіпотеза відкидається. Це рівносильно тому, що у вибірковому просторі виділяється дві множини: множина тих точок із , при яких критерій приймає значення із області прийняття гіпотези, і множина V тих точок із , при яких критерій приймає значення із критичної області.

Ймовірність того, що критерій прийме значення із критичної області, називається рівнем значущості критерію і позначається . Частіше всього задають близьким до 0 і покладають рівним 0,1; 0,05; 0,01; 0,005; 0,001.

Застосування процедури перевірки гіпотези пов’язано із такими помилками: відкинути гіпотезу 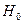, якщо вона правильна (помилка першого роду); прийняти гіпотезу 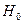, якщо вона неправильна (помилка другого роду). Тобто, у двох випадках ми приймаємо правильне рішення – правильна гіпотеза приймається або неправильна відкидається; і у двох випадках неправильне рішення – правильна гіпотеза відкидається або неправильна приймається. Ймовірність того, що правильна гіпотеза відкидається – це рівень значущості критерію. При побудові процедури перевірки гіпотези необхідно домагатися мінімальних значень ймовірностей помилок обох родів.

Якщо експериментальні дані не узгоджуються із гіпотезою за вибраним критерієм, то це означає, що критерій приймає значення із критичної області. Тоді з ймовірністю помилки першого роду спостерігається подія, яка протирічить гіпотезі. Якщо ймовірність такої події мала, то це означає, що спостерігається практично неможлива подія. В цьому випадку гіпотеза має бути відкинута з практичною достовірністю. Якщо експериментальні дані узгоджуються із висунутою гіпотезою, то це ще не означає, що вони не будуть узгоджуватися із іншою гіпотезою. При перевірці статистичних гіпотез за результатами спостережень неможливо довести справедливість гіпотези, можна лише стверджувати, що статистичні дані не протирічать висунутій гіпотезі. Отже, висновки, які приймаються на основі статистичних даних, формулюються у такому вигляді: експериментальні дані узгоджуються із даною гіпотезою, протирічать даній гіпотезі.

Із сказаного випливає, що перевірку статистичної гіпотези можна проводити за такою схемою: вияснення змісту гіпотези і вибір критерію для перевірки статистичної гіпотези; знаходження розподілу критерію, якщо розподіл спостережень співпадає з гіпотетичним; за заданим рівнем значущості виділяють область прийняття гіпотези і критичну область або знаходять критичні точки критерію, тобто точки, які відділяють критичну область і область прийняття гіпотези; за результатами спостережень знаходять спостережуване значення критерію , якщо спостережуване значення критерію попадає в область прийняття гіпотези, то гіпотезу приймають, у протилежному випадку – відкидають.

Критерієм називають також і правило, яке дозволяє за вибіркою (x₁,…,x_n) прийняти або основну гіпотезу H₀, або альтернативну H₁. Кожен критерій однозначно визначається заданням критичної множини V , де V – прообраз області S при відображенні K=K(x₁,…,x_n). Попадання вибіркової точки (x₁,…,x_n) у V свідчить про те, що статистичні дані не узгоджуються із гіпотезою H₀. Можна різними способами вибирати множину V, щоб виконувалась умова (ймовірність помилки першого роду дорівнювала )

.

Розглянемо тепер ймовірність помилки другого роду (прийняти гіпотезу H₀, якщо вона неправильна)

.

Оскільки

,

то

називають потужністю критерію. Отже, задача знаходження критерію (знаходження критичної множини V, множину V також називають критерієм), що має найменшу ймовірність помилки другого роду, є задачею знаходження критерію, що має найбільшу потужність (найбільш потужного критерію).

Критерій V називається найбільш потужним, якщо для довільної множини такої, що ,

.

Розглянемо задачу вибору із двох простих гіпотез. Нехай і . Множину V необхідно вибрати так, щоб ймовірність попадання вибіркової точки у V була малою, якщо H₀ правильна, і великою, в протилежному випадку. Задамо .

Множину V необхідно вибрати так, щоб потужність критерію була максимальною для довільного допустимого значення .

Нехай – щільність розподілу (або розподіл у дискретному випадку) досліджуваної випадкової величини у випадку справедливості гіпотези H_i (i=0;1). Розглянемо множину X тих точок (x₁,…,x_n), для яких

, (16)

де – довільна стала.

Щільність називається функцією вірогідності гіпотези H_i (i=0;1), а відношення 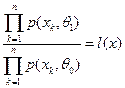називають відношенням вірогідності. Критерій із критичною множиною X називають критерієм відношення вірогідності. Множина X залежить від c, тому 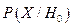= g(c) є функцією від с. Функція g(c) є незростаючою (при c₁<c₂ ), g(c) , g(0)=1. Оскільки

,

то . Отже при 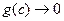. Будемо вважати, що існує таке с, для якого (ця умова не є необхідною). Ця умова виконується, якщо g(c) неперервна. Якщо ж g(c) має в точці с розрив, то визначення X змінюємо, виключаючи з неї ті точки (x₁,…,x_n), для яких в (16) виконується рівність. Для множини X, що відповідає вибраному с .

Теорема (Неймана – Пірсона). Серед всіх критеріїв із заданим рівнем значущості , що перевіряють дві прості гіпотези H₀ і H₁, критерій відношення вірогідності є найбільш потужним.

Розглянемо приклад застосування теореми. Нехай досліджується випадкова величина, що має нормальний розподіл із параметрами і ( – відома). Розглянемо гіпотези 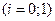, 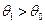. Тоді

і нерівність еквівалентна нерівності

,

яку можна подати у вигляді

.

При справедливості основної гіпотези, величина 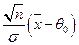має стандартний нормальний розподіл ( – відповідна функція розподілу), тому

.

При функція – неперервна, тому також неперервна і для заданого 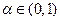однозначно визначається величина така, що , .

Отже, найбільш потужний критерій для перевірки гіпотези при альтернативній задається критичною областю

, .

Знайдемо потужність одержаного критерію

.

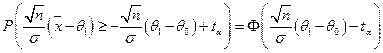Крім критеріїв перевірки гіпотез, що основані на вибірках фіксованого обсягу, існують послідовні критерії. При використанні цих критеріїв, випробування проводяться послідовно і після кожного випробування робиться висновок про прийняття однієї із гіпотез або продовження випробувань.

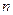Перевірка гіпотез про рівність ймовірностей. Нехай задано деяку сукупність однорідних об’єктів. Необхідно перевірити гіпотезу – доля об’єктів із заданою властивістю дорівнює заданому числу . У зв’язку з цим розглянемо просту гіпотезу при альтернативній гіпотезі . Нехай проведено експериментів, у яких подія настала разів. Ймовірність є невідомою, але відносна частота є незміщеною і спроможною оцінкою невідомої ймовірності , тому ми можемо порівняти відносну частоту з , де , – число появ події в -му експерименті. При справедливості висунутої гіпотези , , . Для перевірки гіпотези використаємо критерій – випадкову величину . При справедливості гіпотези 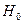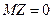, , 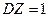тому при великих 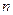велична є асимптотично нормальною (0,1).

Нехай задано рівень значущості . Виберемо критичну точку так, щоб виконувалась умова . Знайшовши із рівняння , ми поділяємо множину всіх значень на область прийняття гіпотези і критичну область. Критична область – це множина тих значень , для яких . За результатами спостережень знаходимо спостережуване значення критерію 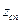. Якщо 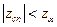, то гіпотезу приймають, у протилежному випадку – відкидають.

Розглянемо просту гіпотезу при альтернативній гіпотезі . В цьому випадку критична область буде односторонньою: це множина тих значень , для яких , а критична точка знаходиться із умови 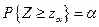. Оскільки , то критичну точку знаходимо із умови . За результатами спостережень знаходимо спостережуване значення критерію 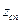. Якщо , то гіпотезу приймають, у протилежному випадку – відкидають.

Нехай розглядаються дві сукупності. Ймовірність настання події в першій сукупності дорівнює , а в другій – . Часто виникає необхідність перевіряти гіпотезу при альтернативі . Нехай в першій сукупності проведено експериментів, в яких подія настала разів, в другій сукупності проведено експерименти, в яких подія настала разів. Тоді оцінками невідомих ймовірностей і будуть відповідні відносні частоти і . Розглянемо різницю . , . При правильності основної гіпотези , 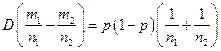. Тому величина 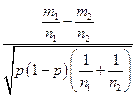буде асимптотично нормальною з параметрами 0 і 1. Якщо гіпотеза правильна, то ми можемо вважати, що проведено спостережень, в яких подія настала раз. Замінимо його оцінкою і для перевірки гіпотези використаємо критерій . Величина є асимптотично нормальною з параметрами 0 і 1. Тому за рівнем значущості можна знайти із умови . За результатами спостережень знаходимо спостережуване значення критерію 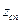. Якщо 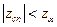, то гіпотезу приймають, у протилежному випадку – відкидають.

Перевірка статистичних гіпотез про рівність середніх двох нормально розподілених випадкових величин. Нехай 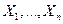і дві незалежні нормально розподілені вибірки із параметрами 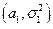і відповідно. Нехай параметри і 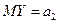невідомі. Часто на практиці виникає потреба встановити, чи суттєво відрізняються середні в цих вибірках. Тобто необхідно перевірити гіпотезу . Нехай альтернативна гіпотеза має вигляд . У цьому випадку критична область буде симетричною. Нехай дисперсії і 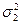відомі. Оскільки величини і незалежні і нормальні , , то при правильності основної гіпотези , а , тому величина

буде мати стандартний нормальний розподіл. За рівнем значущості із рівняння можна знайти (із рівняння ), а за вибірками і знаходимо спостережуване значення критерію 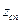. Якщо 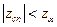, то гіпотеза приймається, інакше - відкидається.

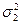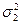
Розглянемо тепер випадок, коли дисперсії і невідомі, але рівні між собою, тобто = . Тоді величина має стандартний нормальний розподіл. Величини і є незміщеними та спроможними оцінками дисперсій і . Тоді величина буде мати розподіл , а величина буде мати розподіл . Тому величина буде мати розподіл . Звідси випливає, що величина

буде мати розподіл Стьюдента із ступенями вільності. Отже, для перевірки гіпотези одержуємо критерій

,

що має розподіл Стьюдента з ( ) ступенями вільності.

За рівнем значущості і числом ступенів вільності можна знайти таку точку 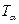, щоб 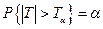. А за вибірками і знаходимо , , , і спостережуване значення критерію . Якщо , то гіпотеза приймається, в протилежному випадку – відкидається.

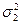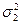
Перевірка гіпотез про рівність дисперсій двох нормально розподілених випадкових величин. У попередньому пункті ми робили припущення, що дисперсії і невідомі, але рівні між собою: = . Тому для застосування критерію Стьюдента необхідно спочатку перевірити гіпотезу про рівність дисперсій. Нехай знову 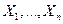і – дві незалежні нормально розподілені вибірки із параметрами 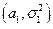і відповідно. Розглянемо гіпотезу при альтернативній гіпотезі . Незміщеними і спроможними оцінками для дисперсій є відповідні виправлені дисперсії і . Оскільки досліджувані величини і мають нормальний розподіл, то величини і мають розподіли відповідно з ( ) та ( ) ступенями вільності. Тоді величина буде мати розподіл Фішера з ступенями вільності. Тобто, для перевірки гіпотез про рівність дисперсій, використовуємо критерій Фішера

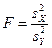
з ступенями вільності.

За результатами спостережень знаходимо і , якщо поділимо більшу із виправлених дисперсій на меншу, то одержимо спостережуване значення критерію . За рівнем значущості і ступенями вільності можна знайти критичну точку із умови , де 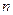- обсяг вибірки, за якою знайдена більша виправлена дисперсія, а – менша. У випадку гіпотеза приймається, інакше – відкидається.

Перевірка гіпотез про вигляд розподілу. Критерії перевірки гіпотез про вигляд розподілу називають критеріями згоди. Ми розглянемо критерій Колмогорова і критерій . Критерій Колмогорова оснований на теоремі Колмогорова.

Теорема. Нехай – неперервна функція розподілу, а – емпірична функція розподілу, що знайдена за вибіркою із розподілу . Позначимо . Тоді

де – функція Колмогорова.

Нехай перевіряється гіпотеза про те, що є вибіркою із розподілу . За вибіркою знаходимо емпіричну функцію розподілу . При великих 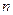граничну функцію можна використовувати для практичних розрахунків, тобто досить добре наближує ймовірність , тому для перевірки гіпотези можна використати статистику . Граничний розподіл не залежить від вигляду розподілу . Важливим є і те, що розподіл величини при великих 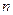(уже при ) практично не залежить від 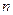. Оскільки емпірична функція розподілу збігається до відповідної теоретичної функції розподілу, то критична точка за рівнем значущості визначається із умови . Враховуючи наближену рівність , критичну точку можна знайти із рівняння (наприклад, , , 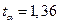). Для знаходження спостережуваного значення критерію за вибіркою , для кожної із точок знайдемо спочатку різниці , . Значення дорівнює найбільшій із цих різниць. Тоді спостережуване значення критерію . Якщо , то гіпотезу приймають, інакше – відкидають.

Досить широке використання в статистиці знайшов критерій (критерій Пірсона), що оснований на порівнянні емпіричних та теоретичних частот.

Нехай перевіряється гіпотеза про те, що є вибіркою із розподілу . Нехай множина значень досліджуваної величини розбита на підмножин: 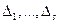. Позначимо через число результатів спостережень 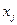, які попадають до , , тоді називають емпіричними частотами. Оскільки гіпотеза стверджує, що досліджувана величина має розподіл , то за розподілом можна знайти ймовірності . Тоді називають теоретичними частотами. Із закону великих чисел, теорема Бореля, випливає, що при справедливості основної гіпотези з ймовірністю одиниця. Тобто, при великих 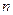, різниці будуть невеликими.

Розглянемо випадкову величину . Можна довести, що при розподіл величини збігається до розподілу з ( ) ступенями вільності. На практиці граничний розподіл можна використовувати із гарним наближенням уже при і .

Величина є невід’ємною. За рівнем значущості і числом ступенів вільності ( ) із рівняння знаходимо . За результатами спостережень знаходимо спостережуване значення критерію . Якщо , то гіпотеза приймається, інакше – відкидається.

Приклад. В експериментах з селекцією гороху Мендель спостерігав частоти різного вигляду насіння, що одержані при схрещуванні рослин з круглим жовтим і зморшкуватим зеленим насінням. Ці дані та значення теоретичних ймовірностей, що визначаються за теорією спадковості Менделя, наведені в таблиці:

Насіння	Частота	Ймовірність
Кругле жовте		9/16
Зморшкувате жовте		3/16
Кругле зелене		3/16
Зморшкувате зелене		1/16
Всього

При рівні значущості перевірити гіпотезу про узгодження експериментальних даних із теоретичними ймовірностями.

За результатами спостережень знаходимо спостережуване значення критерію

.

За рівнем значущості і числом ступенів вільності 4-1=3 за таблицею розподілу знаходимо . Оскільки , то можна зробити висновок, що експериментальні дані добре узгоджуються із теоретичними ймовірностями.

При великих значеннях , розподіл можна наближено замінити нормальним розподілом із середнім ( ) і дисперсією .

Нехай розподіл 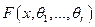залежить від параметрів. Тоді на основі результатів спостережень ми можемо замінити невідомі параметри їх відповідними оцінками і на основі функції знаходимо теоретичні частоти . Тоді при розподіл величини збігається до розподілу з ( ) ступенями вільності, де – число оцінюваних параметрів розподілу. А далі процедура перевірки гіпотези така ж сама.