
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Необходимые и достаточные условия
|
|
2.1.1. (Необходимое условие экстремума первого порядка) Пусть X*ÎRп - точка локального минимума (максимума) функции f(X) на множестве Rп и f(X) дифференцируема в точке X*. Тогда градиент функции f(X) в точке X* равен нулю:
Ñf(X*)=0, (2.1.1)
что равносильно системе
 =0, i=1, 2, …, n. (2.1.2)
=0, i=1, 2, …, n. (2.1.2)
2.1.2. (Необходимое условие экстремума второго порядка) Пусть X*ÎRп - точка локального минимума (максимума) функции f(X) на множестве Rп и f(X) дважды дифференцируема в точке X*. Тогда матрица Гессе, вычисленная в точке X*, является положительно (отрицательно) полуопределённой:
H(X*)³0 (2.1.3)
(H(X*)£0) (2.1.4)
Точки, удовлетворяющие условиям (2.1.1), (2.1.2), (2.1.3) или (2.1.4), называются стационарными.
Условия 2.1.1 и 2.1.2 являются необходимыми условиями экстремума, но не достаточными. Действительно, для функции f(X)=  -
-  точка X*=(0, 0) является стационарной точкой, так как
точка X*=(0, 0) является стационарной точкой, так как
 ,
,  =0 Û (3
=0 Û (3  , 3
, 3  )=0 Û (х1, х2)=0
)=0 Û (х1, х2)=0
(то есть выполняются условия (2.1.1) и (2.1.2)), а также
 =6х1,
=6х1,  =6х2,
=6х2,  =
=  =0, H(X*)=
=0, H(X*)=  .
.
(то есть выполняются условия (2.1.3) и (2.1.4)). Но эта точка не является точкой экстремума, так как существуют точки X1 и X2, в которых имеют место неравенства f(X1)<f(X*)<f(X2): достаточно взять X1=(0; e) и X2=(e; 0), где e>0 - сколь угодно малое число.
Для того, чтобы проверить, является ли стационарная точка точкой экстремума, используются следующие достаточные условия экстремума:
2.1.3. (Достаточные условия экстремума) Пусть функция f(X) в точке X* дважды дифференцируема, Ñf(X*)=0 и H(X*)>0 (H(X*)<0). Тогда точка X* является точкой локального минимума (максимума) функции f(X) на Rп.
Таким образом, для того, чтобы исследовать функцию на безусловный экстремум (то есть найти для функции точки экстремумов, определить их характер и вычислить значения функции в этих точках), достаточно:
1. Найти у функции частные производные первого порядка.
2. Решив систему (2.1.2), найти стационарные точки функции.
3. Найти у функции частные производные второго порядка и составить матрицу Гессе H(X).
4. Определить, какие из стационарных точек являются точками максимума, какие - точками минимума, какие - ни тем, ни другим. Для этого используем информацию о знакоопределённости матрицы Гессе в стационарных точках (критерии 1.6.1 или 1.6.2из Главы I).
5. Вычислить значения функции в точках экстремумов.
Пример I. Исследовать функцию f(X)=3x1x2-x1  -
-  x2 на безусловный экстремум.
x2 на безусловный экстремум.
Решение. Следуем вышеописанной схеме исследования функции на безусловный экстремум.
1. Найдём у функции частные производные первого порядка:  =3x2-
=3x2-  -2x1x2,
-2x1x2,  =3x1-2x1x2-
=3x1-2x1x2-  .
.
2. Решая систему (2.1.2), найдём стационарные точки функции:
 Û
Û 
Вычитая из первого уравнения системы второе, приходим к уравнению 3x2-3x1-  +
+  =0. Дальнейшие очевидные преобразования приводят к уравнению (x2-x1)(3-x2-x1)=0. Дальше рассмотрим отдельно два случая:
=0. Дальнейшие очевидные преобразования приводят к уравнению (x2-x1)(3-x2-x1)=0. Дальше рассмотрим отдельно два случая:
Случай 1. x2-x1=0, то есть x2=x1. Подставляя это равенство, например, в первое уравнение системы, получаем уравнение 3x1-3  =0, решениями которого являются x1=0 и x1=1. Тогда решениями системы являются Х1=(0, 0) и Х2=(1, 1).
=0, решениями которого являются x1=0 и x1=1. Тогда решениями системы являются Х1=(0, 0) и Х2=(1, 1).
Случай 2. 3-x2-x1=0, то есть x2=3-x1. Подставляя это равенство во второе уравнение системы, получаем уравнение -3x1+  =0, решениями которого являются x1=0 и x1=3. Тогда решениями системы являются Х3=(0, 3) и Х4=(3, 0).
=0, решениями которого являются x1=0 и x1=3. Тогда решениями системы являются Х3=(0, 3) и Х4=(3, 0).
3. Найдём у функции частные производные второго порядка и составим матрицу Гессе H(X):
 =-2х2,
=-2х2,  =-2х1,
=-2х1,  =
=  =3-2(x1+x2), H(X)=
=3-2(x1+x2), H(X)= 
4. Определим, какие из стационарных точек являются точками максимума, какие - точками минимума, какие - ни тем, ни другим. Для этого используем информацию о знакоопределённости матрицы Гессе в стационарных точках (критерии 1.6.1 или 1.6.2 из Главы I).
H(X1)=  .
.
Составим характеристическое уравнение и решим его:
 =0 Û
=0 Û  =0 Û (l2-9)=0 Û l1=3, l2=-3.
=0 Û (l2-9)=0 Û l1=3, l2=-3.
Так как собственные значения матрицы H(X1) имеют разные знаки, то матрица H(X1) - знаконеопределённая (см. 1.6.2 из Главы I и 1.1.2), а точка X1 не является точкой экстремума.
Для точки X2 имеем
H(X2)=  , D1=-2<0, D2=
, D1=-2<0, D2=  =3>0.
=3>0.
Так как угловые миноры матрицы Гессе знакочередуются, начиная с «-», то она является отрицательно определённой и по 2.1.3 точка X2 является точкой локального максимума.
Для точек X3 и X4 имеем H(X3)= 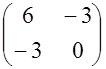 и H(X4)=
и H(X4)=  , и у них множества собственных значений {l1, l2}={3+
, и у них множества собственных значений {l1, l2}={3+  , 3-
, 3-  } совпадают, а сами значения имеют различные знаки. Поэтому матрицы Гессе для этих точек являются знаконеопределёнными, и точки не являются точками экстремума.
} совпадают, а сами значения имеют различные знаки. Поэтому матрицы Гессе для этих точек являются знаконеопределёнными, и точки не являются точками экстремума.
Таким образом, из стационарных точек только точка X2 является точкой экстремума - максимума.
5. Значение функции в этой точке - f(X2)=3×1×1-1×12-12×1=1.
Заметим, что f(X)=x1x2(3-x1-x2), и при отрицательных x1 и x2, достаточно больших по абсолютной величине, f(X)>1. Например, f(-2, -2)=(-2)(-2)(3-(-2)-(-2))=28>1. Найденная точка максимума имеет только локальный характер.
Ответ: (1, 1) - точка локального максимума, fmax(X)=1.
Пример II. Исследовать функцию f(X) на безусловный экстремум:
а) f(X)=-  -2
-2  -3
-3  -x1-2x2+x1x2;
-x1-2x2+x1x2;
б) f(X)=2  +2
+2  +3
+3  -2x1+3x2+2x1x3;
-2x1+3x2+2x1x3;
в) f(X)=  +2
+2  -
-  +4x1+x2-2x1x2.
+4x1+x2-2x1x2.
Решение. Действуем по схеме решения предыдущего примера.
а) 1. Найдём у функции частные производные первого порядка:  =-2x1-1+x2,
=-2x1-1+x2,  =-4x2-2+x1,
=-4x2-2+x1,  =-6x3.
=-6x3.
2. Решая систему (2.1.2), найдём стационарные точки функции:
 Û
Û  Û
Û 
Из последнего уравнения получаем x3=0, а первые два рассматриваем как отдельную систему из двух уравнений с двумя неизвестными, и решаем, например, правилом Крамера:
D=  =7,
=7,  =
=  =-6,
=-6,  =
=  =-5,
=-5,
x1=  =
= 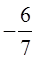 , x2=
, x2=  =
=  .
.
Таким образом, X0=  ,
,  - стационарная точка функции.
- стационарная точка функции.
3. Найдём у функции частные производные второго порядка и составим матрицу Гессе H(X):
 =-2,
=-2,  =-4,
=-4,  =-6,
=-6,  =
=  =1,
=1,
 =
=  =1,
=1,  =
=  =0,
=0,
H(X)= 
4. Определим, является ли стационарная точка точкой экстремума, и если да, то какой вид экстремума достигается в точке. Для этого исследуем на знакоопределённость матрицы Гессе, например, используя угловые миноры:
D1=-2<0, D2=  =7>0, D3=
=7>0, D3=  =-42<0,
=-42<0,
то есть D1<0, D2>0, D3<0. Следовательно, H(X)<0 (матрица Гессе отрицательно определённая), и по 2.1.3 точка X0=  ,
,  является точкой максимума.
является точкой максимума.
5. Вычислим значение функции в этой точке:
fmax=f(X0)=f  ,
,  =-
=-  -2×
-2×  -3×02-
-3×02-  -2×
-2×  +
+  ×
×  =
=  .
.
б) Действуем по схеме решения задачи, опуская комментарии:
1.  =4x1-2+2x3,
=4x1-2+2x3,  =4x2+3,
=4x2+3,  =6x3+2x1.
=6x3+2x1.
2.  Û
Û  Û
Û  Þ x2=
Þ x2=  .
.
Найдём x1 и x3:
 Û
Û 
D=  =5,
=5,  =
=  =3,
=3,  =
=  =-1,
=-1,
x1=  =
=  , x2=
, x2=  =
=  , X0=
, X0=  ,
,  - стационарная точка.
- стационарная точка.
3.  =4,
=4,  =4,
=4,  =6,
=6,  =
=  =0,
=0,  =
=  =2,
=2,  =
=  =0, H(X)=
=0, H(X)=  .
.
4. D1=4>0, D2= 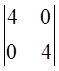 =16>0, D3=
=16>0, D3=  =80>0, H(X)>0 (матрица Гессе положительно определённая), и X0=
=80>0, H(X)>0 (матрица Гессе положительно определённая), и X0=  ,
,  - точка минимума.
- точка минимума.
5. fmax=f(X0)=f  ,
,  =
=
=2×  +2×
+2×  +3×
+3×  -2×
-2× 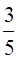 +3×
+3×  +2×
+2× 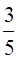 ×
×  =
=  .
.
в) Как и выше:
1.  =2x1+4-2x2,
=2x1+4-2x2,  =4x2+1-2x1,
=4x2+1-2x1,  =-2x3.
=-2x3.
2.  Û
Û 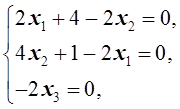 Û
Û  Þ x3=0.
Þ x3=0.
Найдём x1 и x2:
 Û
Û  Û
Û 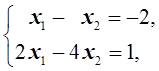
D=  =-2,
=-2,  =
= 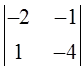 =9,
=9,  =
=  =5,
=5,
x1=  =
=  , x2=
, x2=  =
=  , X0=
, X0=  ,
,  - стационарная точка.
- стационарная точка.
3.  =2,
=2,  =4,
=4,  =-2,
=-2,  =
=  =-2,
=-2,  =
=  =0,
=0,  =
=  =0, H(X)=
=0, H(X)=  .
.
4. D1=2>0, D2=  =4>0, D3=
=4>0, D3= 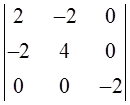 =-8<0, то есть D1>0, D2>0, D3<0, и матрица Гессе знаконеопределённая. Следовательно, X0=
=-8<0, то есть D1>0, D2>0, D3<0, и матрица Гессе знаконеопределённая. Следовательно, X0=  ,
,  точкой экстремума не является.
точкой экстремума не является.
Ответ: а) fmax=  достигается в точке X0=
достигается в точке X0=  ,
,  ;
;
б) fmin=  достигается в точке X0=
достигается в точке X0=  ,
,  ;
;
в) точки экстремума у функции не существует.
Пример III. Исследовать функцию
f(X)=2  +
+  +
+  +x1x3-12x2+5x3+6
+x1x3-12x2+5x3+6
на безусловный экстремум.
Решение. 1. Найдём у функции частные производные первого порядка:  =4x1+x3,
=4x1+x3,  =3
=3  -12,
-12,  =2x3+x1+5.
=2x3+x1+5.
2. Найдём стационарные точки функции:
 Û
Û  Û
Û  Þ x2=±2.
Þ x2=±2.
Отдельно ищем x1 и x3: 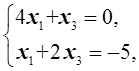 D=
D=  =7,
=7,  =
=  =5,
=5,  =
=  =-20, x1=
=-20, x1=  =
=  , x2=
, x2=  =
=  .
.
Таким образом, X1=  ,
,  , X0=
, X0=  ,
,  - стационарные точки функции.
- стационарные точки функции.
3. Составим матрицу Гессе H(X):
 =4,
=4,  =6x2,
=6x2,  =2,
=2,  =
=  =0,
=0,
 =
=  =1,
=1,  =
=  =0,
=0,
H(X)=  .
.
4. Определим, какие из стационарных точек X1 и X2 являются точками максимума, какие - точками минимума, какие - ни тем, ни другим. Для этого используем информацию о знакоопределённости матрицы Гессе в стационарных точках.
Имеем H(X1)=  , и
, и
D1=4>0, D2=  =48>0, D3=
=48>0, D3= 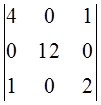 =84>0,
=84>0,
и H(X1)>0. Значит, точка X1=  ,
,  - точка минимума.
- точка минимума.
Далее, H(X2)=  , и
, и
D1=4>0, D2=  =-48<0, D3=
=-48<0, D3=  =-84<0,
=-84<0,
то есть D1>0, D2<0, D3<0, и H(X1) является знаконеопределённой. Это означает, что точка X2=  ,
,  не является точкой экстремума.
не является точкой экстремума.
Таким образом, из стационарных точек только X1 является точкой экстремума, причём является точкой минимума.
5. Вычислим значение функции в точке X1:
fmin=f(X1)=f  ,
,  =2×
=2×  +23+
+23+  +
+ 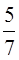 ×
×  -12×2+5×
-12×2+5×  +6=-
+6=-  .
.
Ответ: fmin=-  достигается в точке X1=
достигается в точке X1=  ,
, 
2.2. Упражнение.Исследовать функцию f(X) на безусловный экстремум:
а) f(X)=2  +5
+5  +
+  -3x1x2-2x2+x3;
-3x1x2-2x2+x3;
б) f(X)=3  +2
+2  +
+  +x1x3+2x2-3x3;
+x1x3+2x2-3x3;
в) f(X)=2  +3
+3  +4
+4  -2x1x2-4x2+3x2;
-2x1x2-4x2+3x2;
г) f(X)=2  -5
-5  +
+  -3x1x2-2x2+x3;
-3x1x2-2x2+x3;
д) f(X)=-3  +2
+2  +
+  +x1x3+2x2-3x3;
+x1x3+2x2-3x3;
е) f(X)=2  +3
+3  -4
-4  -2x1x2-4x2+3x2;
-2x1x2-4x2+3x2;
ж) f(X)=-2  -5
-5  -
-  -3x1x2-2x2+x2;
-3x1x2-2x2+x2;
з) f(X)=-3  -2
-2  -
-  +x1x3+2x2-3x3;
+x1x3+2x2-3x3;
и) f(X)=-2  -3
-3  -4
-4  -2x1x2-4x2+3x2;
-2x1x2-4x2+3x2;
к) f(X)=  +2
+2  +3
+3  +x2x3-27x1+5x2-3;
+x2x3-27x1+5x2-3;
л) f(X)=3  +
+  +4
+4  +2x1x2+4x2-48x3+18;
+2x1x2+4x2-48x3+18;
м) f(X)=4  +5
+5  +3
+3  +4x1x3--60x2+4x3-2.
+4x1x3--60x2+4x3-2.
|
Просмотров 1183 |
|
|
