ЭЛЕКТРОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ

Общий случай

Выведенные в предыдущем разделе дифференциальные уравнения позволяют в принципе определить векторы Е и Н через функции j^ст и ρ^ст. Однако наличие в их правых частях выражений gradρ^ст и rotj^ст в ряде случаев несколько затрудняет получение

удобных расчетных формул. Поэтому указанные уравнения обы­чно используют в тех случаях, когда сторонние источники рас­положены за пределами рассматриваемой области, т.е. когда уравнения (2.27) и (2.28) становятся однородными и соответ­ственно уравнения (2.31) и (2.32) переходят в (2.33) и (2.34).

В общем случае для определения векторов поля по заданным источникам обычно применяют искусственный прием: сначала находят вспомогательные функции, а потом через них вычисляют векторы Е и Н. Эти вспомогательные функции можно ввести различным образом в зависимости от специфических особенно­стей анализируемой задачи. Для упрощения решения многих задач вводят так называемые электродинамические потенциалы. Рассмотрим систему уравнений Максвелла (2.25). Последнее уравнение этой системы представляет собой четвертое уравнение Максвелла divВ = 0, записанное для случая однородной изо­тропной среды. Так как дивергенция ротора любого вектора равна нулю (divrota = 0), то из уравнения divВ = 0 следует, что вектор В можно представить в виде В = rotА. При этом вектор

При известном вектореА уравнение (2.35) позволяет одно­значно найти вектор Н. Однако оно допускает некоторый произвол в определении вектора А. Действительно, если вместо А взять вектор A₁= А + grad ψ, где ψ - произвольная скалярная функция, то значение вектора Н не изменится, так как

Неоднозначность определения вектораА будет использована при выводе дифференциального уравнения для А.

Подставим выражение (2.35) во второе уравнение системы (2.25) и изменим порядок дифференцирования по времени и пространственным координатам. Объединив затем векторы Е и дА/дtпод знаком ротора, получим rot(E + дА/дt) = 0. Учитывая тождество (2.36), можно положить, что стоящее под знаком ротора выражение равно - gradи, где и- некоторая скалярная функ­ция, или

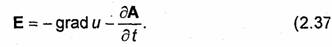
Знак минус перед gradи в формуле (2.37) введен, чтобы в случае электростатического поля функция и совпадала с обычным эле­ктростатическим потенциалом.

Таким образом, все векторы, определяющие электромаг­нитное поле, выражаются через две функции: векторный поте­нциалА и скалярный потенциал и. Следовательно, задача состоит теперь в том, чтобы найти функции А и и. Подставляя (2.35) и (2.37) в первое уравнение системы (2.25) и преобразовывая левую часть получающегося при этом соотношения с помощью тождества (2.26), приходим к равенству

Упростим уравнение (2.38). Как уже отмечалось, векторА определен с точностью до градиента произвольной скалярной функции. Следовательно, можно потребовать, чтобы векторА удовлетворял добавочному условию. Потребуем, чтобы

Соотношение (2.39) принято называть условием калибровки.учетом (2.39) уравнение (2.38) принимает вид

Аналогичное уравнение получается и для скалярного потен­циала и. Подставляя (2.37) в третье уравнение системы (2.25), получаем

Используя условие калибровки (2.39) и тождество divgradи =Δ²u, приходим к уравнению

(2.41)

Таким образом, векторный и скалярный потенциалы, как и векторы Е и Н, удовлетворяют неоднородным уравнениям Даламбера. Однако правые части уравнений для потенциалов имеют более простой вид. Поэтому уравнения (2.40) и (2.41) оказываются более удобными при решении многих конкретных задач.

Найдем частные решения уравнений (2.40) и (2.41), считая функции j^ст и ρ^ст. известными. Вначале рассмотрим уравнение (2.41). Предположим, что электрическое поле создается точечным неподвижным зарядом постоянной величины Q= const, располо­женным в начале координат, вектор Е в этом случае определяется выражением (1.7). Так как поле не должно зависеть от времени, то dA/дt= 0 и соотношение (2.37) принимает видЕ =- gradи. Рас­писывая gradи в сферической системе координат r,θ,φ (см. приложение 4) и учитывая, что вектор Е в рассматриваемом случае может зависеть только от координаты r(от расстояния от заряда Q до точки наблюдения), получаем

где r₀ - координатный орт переменной r. Подставляя выражение (2.42) в (1.7) и выполняя интегрирование по переменной r, находим функцию и:

Постоянная интегрирования в (2.43) принята равной нулю, чтобы при r→ ∞ функция и обращалась в нуль. Формула (2.43) полностью совпадает с известным из курса общей физики вы­ражением для электростатического потенциала точечного заряда (см. замечание по поводу выбора знака перед gradи в выражении (2.37)). Если заряд сосредоточен в малом элементе объема dVс плотностью ρ^ст, то и =ρ^стdV/(4πεR), где R- расстояние от элемента dVдо точки наблюдения. От этой формулы легко перейти к выражению для электростатического потенциала, создаваемого произвольным распределением зарядов в объеме V. В соот­ветствии с принципом суперпозиции получаем

Значение и, определяемое формулой (2.44), можно рассма­тривать как решение уравнения

получающегося из равенства (2.41), если в пос­леднем положить д²u/дt²=0. Уравнение (2.45) называют уравнением Пуассона.

Предположим теперь, что поле также соз­дается точечным зарядом, расположенным в начале координат, но величина этого заряда изменяется со временем Q = Q(t). Тогда в любой точке, кроме начала координат, потен­циал и будет удовлетворять однородному урав­нению Даламбера

Для решения уравнения (2.46) удобно использовать сфери­ческую систему координат r, θ, φ (рис.2.5). Оператор Лапласа Δ² в этой системе координат определяется формулой (П. 18). Так как лоле создается точечным зарядом, расположенным в начале координат, то потенциал и не должен зависеть от углов θ и φ. Поэтому уравнение (2.45) можно переписать в виде

Учитывая, что и переходя от и к функции и₁, связанной с и соотношением u₁ = rи, получаем

Общее решение уравнения (2.47) имеет вид -

произвольные дважды диф­ференцируемые функции аргументов t-rlcи t+rlcсоответ­ственно. В том, что функции f₁(t-r/c) и f₂(t+r/c) удовлетворяют (2.47), можно убедиться непосредственной подстановкой их в это уравнение. Таким образом, скалярный потенциал и можно представить в виде

Первое слагаемое в выражении (2.48) представляет собой волну, распространяющуюся из начала координат вдоль ради­усов r со скоростью света Действительно, функция в фиксированный момент времени tимеет одинаковые значения на сфере радиуса r = const. В момент времени t + Δtфункция принимает то же значение на сфере радиуса r+cΔt, так как t+ Δt-(r+ cΔt)/c= t-r/c. Волны типа принято называть расходящимися сферическими волнами. Соот­ветственно второе слагаемое в выражении (2.48) представляет собой сферическую волну, распространяющуюся из бесконечности со скоростью света с и сходящуюся к началу координат. Отметим существенную особенность функций, описывающих волновые про­цессы. Они всегда содержат множители вида f(t±r/v), характер зависимости которых от расстояния вдоль направления распро­странения волны в фиксированный момент времени повторяет характер их зависимости от времени в фиксированной точке пространства, а v-скорость распространения волны.

Если источники поля сосредоточены в ограниченной области, то сходящаяся сферическая волна может возникнуть только в результате отражения расходящейся сферической волны. Так как пространство считается однородным, то отраженной волны не может быть, и функцию f₂(t +r/с) нужно считать равной нулю. Следовательно, и = f₁(t- r/c)/r. Значения потенциала и должны быть связаны с интенсивностью источников поля. В рассмат­риваемом случае источником поля является точечный заряд Q(t). Полученное выражение дляи должно быть справедливым при любом законе изменения функции Q(t). Так как в статическом случае потенциал и определяется формулой (2.43), естественно предположить, что f₁-r/c) = Q(t-r/c)/(4πε). Тогда u=Q(t-R/c)/(4πεr). Если заряд сосредоточен в малом элементе объема dVс пло­тностью ρ^ст = ρ^ст(t), то скалярный потенциал и = p^СТ(t-R/c)dV/(4πεR), где R-как и ранее, расстояние от элемента dVдо точки наблю­дения. От этой формулы легко перейти к выражению для скалярного потенциала, обусловленного произвольным распреде­лением сторонних зарядов в объеме V:

декартовы координаты элемента dV; x, у, z-декартовы координаты точки наблюдения N; элемент объема (рис.2.6).

Выражение (2.49) является частным решением неоднородного уравнения Даламбера (2.41). Отметим, что приведенный здесь вывод не является строгим, он имеет лишь наводящий характер. Строгий вывод формулы (2.49) можно найти, например, в [12].

Аналогично можно записать и решение уравнения (2.40). Для этого нужно в (2.49) заменить и на А, ρ^ст на j^СТ и ε на 1/μ. В результате получим

Из (2.49) и (2.50) следует, что для вычисления электро­динамических потенциалов ииА в произвольной точке прост­ранства N=N(х, у, z) в момент времени t нужно брать значения токов и зарядов в каждом элементе dVв более ранний по срав­нению с tмомент времени t’=t-R/c, определяемый расстоянием Rот элемента dVдо точки наблюдения N(х, у, z) (рис.2.6). Иными словами, влияние источников электромагнитного поля проявля­ется не мгновенно: требуется некоторое время Δt = Rlc, за которое электромагнитные колебания, вызванные зарядами и токами в элементе dV, успеют распространиться от элемента dVдо точки наблюдения. Поэтому функцииА и и в форме (2.50) и (2.49) часто называют запаздывающими потенциалами.

7.Уравнение баланса мгновенных значений мощности (см. вопрос №3)

Электромагнитное поле является одной из форм материи. Как и любая другая форма материи, оно обладает энергией. Эта энергия может распространяться в про­странстве и преобразовываться в другие формы энергии.

Сформулируем уравнение баланса для мгновенных значений мощности применительно к некоторому объему V, ограниченному поверхностью S (рис.1.23). Пусть в объеме V, заполненном од­нородной изотропной средой, находятся сторонние источники. Из общих физических представлений очевидно, что мощность, выделяемая сторонними источниками, может расходоваться на джоулевы потери и на изменение энергии электромагнитного поля внутри V, а также может частично рассеиваться, уходя в ок­ружающее пространство через поверхность S. При этом должно выполняться равенство

где Р^ст-мощность сторонних источников; Р_П-мощность джоулевых потерь внутри объема V; Р_Σ -мощность, проходящая через поверхность S; W-энергия электромагнитного поля, сосредоточен­ного в объеме V, a dW/dt- мощность, расходуе­мая на изменение энергии в объеме V.

В данном разделе будут использованы уравнения состояния (1.53). Эти уравнения не позволяют учесть потери энергии при поляризации и намагничивании среды. Поэтому слагаемое Р_п в равенстве (1.120) фактически определяет мощность джоулевых потерь в объеме V, обусловленных током проводимости.

Уравнение (1.120) дает только качественное представление об энергетических соотношениях. Чтобы получить количественные соотношения, нужно воспользоваться уравнениями Максвелла. Рассмотрим первое уравнение Максвелла с учетом сторонних то­ков (1.111). Все члены этого уравнения - векторные величины, имеющие размерность А/м².

Чтобы получить уравнение, аналогичное (1.120), нужно видо­изменить первое уравнение Максвелла (1.111) так, чтобы его члены стали скалярными величинами, измеряющимися в ваттах. Для этого достаточно все члены указанного равенства скалярно умножить на вектор Е, а затем проинтегрировать полученное выражение по объему V. После скалярного умножения на вектор Еполучаем

Используя известную из векторного анализа формулу div[E,H]= = Н rot Е - Е rot H, преобразуем левую часть соотношения (1.121) и заменим rot E его значением из второго уравнения Максвелла (1.39):

Подставляя это выражение в (1.121), получаем

В последнем слагаемом в правой части (1.122) изменен порядок сомножителей в скалярном произведении векторов dB/dt и Н. Это допустимо, так как Н dB/dt = дВ/дt· H. Данное изменение не яв­ляется принципиальным и не дает никаких преимуществ при выводе рассматриваемого здесь уравнения баланса для мгно­венных значений мощности. Однако при такой записи во всех членах уравнения (1.122) второй сомножитель (векторы j^ст, j, BDIdt и Н) является вектором, входившим ранее в первое уравнение Максвелла. Это обстоятельство позволит в дальнейшем (см. 1.8.4) несколько упростить вывод уравнения баланса в случае моно­хроматического поля (уравнения баланса комплексной мощности). Интегрируя почленно уравнение (1.122) по объему V, получаем

где направление элемента dS совпадает с направлением внешней нормали к поверхности S. При переходе от.(1.122) к (1.123) ис­пользована теорема Остроградского-Гаусса для перевода объем­ного интеграла от div[E, H] в поверхностный интеграл от вектор­ного произведения [Е, Н]. Введем обозначение

и преобразуем подынтегральное выражение в последнем слагаемом в правой части (1.123):

Подставляя (1.124) и (1.125) в (1.123) и меняя порядок интег­рирования и дифференцирования, получаем

Выясним физический смысл выражений, входящих в уравнение (1.126).

Рассмотрим первое слагаемое в правой части (1.126). Пред­ставим объем V в виде суммы бесконечно малых цилиндров длиной dl, торцы которых (dS) перпендикулярны направлению тока (вектору j). Тогда EjdV = EjdV=(Edl)(jdS) = dUdl = dP_n, где dl =jdS - ток, протекающий по рассматриваемому бесконечно мало­му цилиндру; dU = Edl - изменение потенциала на длине dl, a dP_n-мощность джоулевых потерь в объеме dV. Следовательно, рас­сматриваемое слагаемое представляет собой мощность джоу­левых потерь Р_п в объеме V. Используя соотношение j = σЕ, для Р_пможно получить и другие представления:

Формулы (1.127) можно рассматривать как обобщенный закон Джоуля-Ленца, справедливый для проводящего объема V произ­вольной формы.

Интеграл в левой части (1.126) отличается от первого сла­гаемого в правой части только тем, что в подынтегральное выражение вместо j входит j^cт. Поэтому он должен определять мощность сторонних источников. Будем считать положительной мощность, отдаваемую сторонними токами электромагнитному по­лю. Электрический ток представляет собой упорядоченное дви­жение заряженных частиц. Положительным направлением тока считается направление движения положительных зарядов. Ток отдает энергию электромагнитному полю при торможении обра­зующих его заряженных частиц. Для этого необходимо, чтобы вектор напряженности электрического поля Е имел составляющую, ориентированную противоположно направлению тока, т.е. чтобы скалярное произведение векторов Е и j^ст было отрицательным (E j^ст <0). При этом левая часть равенства (1.126) будет поло­жительной величиной. Таким образом, мгновенное значение мощ­ности, отдаваемой сторонними токами электромагнитному полю в объеме V, определяется выражением

Для уяснения физического смысла последнего слагаемого в правой части уравнения (1.126) рассмотрим частный случай. Предположим, что объем V окружен идеально проводящей обо­лочкой, совпадающей с поверхностью S. Тогда касательная сос­тавляющая вектора Е на поверхности S будет равна нулю. Эле­мент поверхности dSсовпадает по направлению с внешней нор­малью n₀. Следовательно, поверхностный интеграл в уравнении (1.126) будет равен нулю, так как нормальная компонента век­торного произведения [Е, Н] определяется касательными состав­ляющими входящих в него Векторов. Кроме того, предположим, что среда в пределах объема V не обладает проводимостью ( σ = 0). При этом в рассматриваемой области не будет джоулевых потерь, и первый интеграл в правой части уравнения (1.126) также будет равен нулю. В результате получим

Очевидно, что в рассматриваемом случае мощность сто­ронних источников может расходоваться только на изменение энергии электромагнитного поля. Таким образом, правая часть равенства (1.129) представляет собой скорость изменения энергии электромагнитного поля, запасенной в объеме V, т.е. соответ­ствует слагаемому dW/dt в уравнении (1.126). Естественно пред­положить, что интеграл в правой части (1.129) равен энергии электромагнитного поля, сосредоточенного в объеме V:

Строго говоря, этот интеграл может отличаться от W на не­которую функцию g = g(х, у, z), не зависящую от времени. Не­трудно убедиться, что функция д равна нулю. Перепишем (1.130) в виде W=W^Э+W^М, где

Предположим, что электрическое и магнитное поля являются постоянными (не зависят от времени). В этом случае, как известно из курса физики (см. также гл.З и 4), выражения (1.131) и (1.132) определяют энергию соответственно электрического и магнитного полей в объеме V. Но это означает, что g = 0 и указанные вы­ражения определяют мгновенные значения энергии электричес­кого и магнитного полей в объеме V при любой зависимости от временила их сумма, определяемая формулой (1.130), дейст­вительно равна мгновенному значению энергии электромагнитного поля в объеме V.

Осталось выяснить физическую сущность поверхностного ин­теграла в уравнении (1.126). Предположим, что в объеме V от­сутствуют потери и, кроме того, величина электромагнитной энер­гии остается постоянной (W= const). При этом уравнение (1.126) принимает вид

В то же время из физических представлений очевидно, что в данном частном случае вся мощность сторонних источников должна уходить в окружающее пространство (Р^ст = Р_Σ). Следо­вательно, правая часть уравнения (1.133) равна потоку энергии через поверхность S (пределу отношения количества энергии, проходящей через S за время Δt при Δt→0), т.е.

Естественно предположить, что вектор Ппредставляет собой плотность потока энергии (предел отношения потока энергии через площадку ΔS, расположенную перпендикулярно направлению ра­спространения энергии, к ΔS при ΔS →0). Формально матема­тически это предположение не очевидно, так как замена вектора П на П₁ = П + rot а, где а - произвольный вектор, не изменяет ве­личину Р_Σ. Однако оно является верным и в частности, непо­средственно вытекает из релятивистской теории электромаг­нитного поля [11].

Таким образом, равенство (1.126) аналогично (1.120) и пред­ставляет собой уравнение баланса мгновенных значений мощ­ности электромагнитного поля. Оно было получено Пойнтингом в 1884 г. и называется теоремой Пойнтинга. Соответственно век­тор П называют вектором Пойнтинга. Часто используют также названия "теорема Умова-Пойнтинга" и "вектор Умова-Пойн-тинга" с целью подчеркнуть тот факт, что формулировка закона сохранения энергии в общей форме с введением понятия потока энергии и вектора, характеризующего его плотность, впервые была дана Н.А. Умовым в 1874 г.

Отметим, что энергия может поступать в объем V не только от сторонних источников. Например, поток энергии через поверхность S может быть направлен из окружающего пространства в объем V. При этом мощность P_Σ будет отрицательной, так как положи­тельным считается поток энергии, выходящий из объема V в окружающее пространство (направление элемента dS совпадает с направлением внешней нормали к поверхности S).

Сторонние источники могут не только отдавать энергию, но и получать ее от электромагнитного поля. При этом мощность сто­ронних источников будет отрицательной. Действительно, элект­ромагнитное поле отдает энергию току проводимости, если оно ускоряет движение заряженных частиц, образующих ток. Для этого вектор напряженности электрического поля Е должен иметь сос­тавляющую, ориентированную вдоль линий тока, т.е. чтобы ска­лярное произведение векторов Е и j^ст было больше нуля.

Рассмотрим более подробно формулы, определяющие энер­гию электромагнитного поля. Подынтегральные выражения в

можно интерпретировать как мгновенные значения объемных плотностей энергии элект­рического и магнитного полей соответственно, а их сумму

- как объемную плотность полной энергии электромагнитного поля.

Подчеркнем, что принцип суперпозиции, которому удовле­творяют векторы напряженностей электрического и магнитного полей, не распространяется на энергию. Действительно, пусть энергии полей E₁, H₁ и Е₂, Н₂, существующих по отдельности в области V, равны соответственно W₁ и W₂. Тогда энергия сум­марного поля Е = Е₁ + Е₂, Н = Н₁ + Н₂ определится выражением

- взаимная энергия полей. Взаимная энергия W₁₂ может быть как положительной, так и отрицательной. Если векторы Е₁и Е₂, а также H₁ и Н₂ взаимно перпендикулярны, то W₁₂ = 0.

В случае переменных процессов распределение электро­магнитной энергии непрерывно изменяется. Это изменение в каждой данной точке можно определить на основе уравнения (1.122), которое удобно представить в виде

где p^ст =-E j^ст и p_n = Ej-мгновенные значения плотностей мощности сторонних источников и мощности джоулевых потерь соответственно. При переходе от соотношения (1.122) к уравнению (1.136) учтены формулы (1.125) и (1.135). Уравнение (1.136) является дифференциальной формой теоремы Пойнтинга.