Единственность решения внешних задач электродинамики

В случае внешней задачи электродинамики поверхность S не охватывает рассматриваемую часть пространства, простираю­щуюся до бесконечности. Поэтому для единственности решения кроме одного из условий (2.1)-(2.4) требуется задать допол­нительное условие, характеризующее поведение векторов Е и Н в точках, бесконечно удаленных от поверхности S. Выясним, каким должно быть это дополнительное условие.

Пусть на S выполняется одно из условий (2.1)-(2.4). Предположим, что имеется два решения задачи E_1, H₁ и Е₂, Н₂, и введем в рассмотрение разностное поле Е₃, Н₃ по формулам (2.6). Как и в случае внутренней задачи электродинамики, векторы

Ё₃ и Н₃ удовлетворяют уравнениям Максвелла (2.9) и одному из условий (2.10)—(2.13) на поверхности S. Из произвольной точки 0 внутри области V мысленно проведем сферу радиуса г так, чтобы вся область V и все сторонние источники оказались внутри этой сферы. Объем, заключенный между поверхностями S и S', обозначим через V (рис.2.1). Составим уравнение баланса для средних за период значений мощности поля Ё₃,Н₃ в объеме V:

Перейдем в уравнении (2.18) к пределу при r→ ∞. Тогда область V распространится на все пространство, внешнее по отношению к области V. Если в пределе третье слагаемое в левой части уравнения (2.18) окажется равным нулю, то получающееся при этом соотношение

не будет иметь принципиальных отличий от аналогичного уравне­ния (2.14) для внутренней задачи электродинамики, и, следова­тельно, рассматриваемая задача также будет иметь единственное решение. Действительно, при выполнении условий (2.1)-(2.3), вто­рое слагаемое в левой части (2.19) обращается в нуль, и это урав­нение принимает вид

В частном случае, когда потери в среде обусловлены только нали­чием проводимости, т.е. когда уравнение (2.20) записывается в форме

Так как а 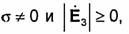то из (2.21) получаем Ё₃ =0, а из второго

уравнения Максвелла - Н₃ = 0. Следовательно, Ё₂ = Ё₁ и Н₂ = Н₁.

Если на поверхности S выполняется условие (2.4), то из урав­нений (2.19) и (2.13) имеем

откуда также следует единственность решения.

В более общем случае, когда един­ственность решения доказывается также на основе формулы (2.20) для краевых условий (2.1)-(2.3) и на основе уравнения (2.19) в случае краевого условия (2.4). При этом должно быть использо­вано соотношение (1.156).

Найдем условие, при котором

и, следовательно, проведенное выше доказательство справедли­во. При r→ ∞ поверхность S' возрастает пропорционально r². По­этому для выполнения условия (2.22) необходимо, чтобы абсолютная величина произведения [Ё₃,Нз] при r→ ∞ убывала быстрее r^-2. Для этого достаточно потребовать, чтобы искомые векторы Е и Н убывали быстрее, чем 1/r.

Таким образом, внешняя задача электродинамики имеет единственное решение, если на поверхности S, ограничивающей объем V, выполняется одно из условий (2.1)-(2.4) и, кроме того, при r→ ∞ векторы Е и Н убывают быстрее, чем 1/r. Последнее все­гда имеет место, так как в любых реальных средах имеются поте­ри энергии.

Отметим, что теорему единственности для внешней задачи электродинамики можно доказать и в случае среды без потерь, если вместо условия убывания векторов Е и Н при r→ ∞ быстрее 1/г потребовать выполнения следующих условий:

Предельные соотношения (2.23) называются условиями излу­чения. Они были сформулированы Зоммерфельдом. Физически эти условия эквивалентны требованию, чтобы при r→ ∞ поле имело характер поперечных волн, распространяющихся вдоль направле­ния r₀ (предполагается, что источники поля находятся на конечном расстоянии от поверхности S). Использованный здесь термин "по­перечная волна" определен в гл.5.

Отметим, что в тех случаях, когда поверхность S имеет особенности типа из­ломов, острых кромок и др., для единственности решения краевой задачи электро­динамики перечисленных условий недостаточно. Необходимо выполнение допол­нительных условий, определяющих поведение составляющих векторов Е и Н вбли­зи этих особенностей.

К таким условиям относятся, в частности, "условия на ребре", сформулиро­ванные Мейкснером для случая идеально проводящих тел. Рассмотрим эти усло­вия. Пусть контур Со представляет собой ребро (острую кромку) идеально проводящей поверхности S. Введем систему координат (рис. 2.2), связанную с контуром Со, где s - длина дуги, отсчитываемая вдоль контура Со от некоторой точки О _Є Со, а - полярные координаты в плоскости, перпендикулярной Со. Ус­ловия на ребре записываются в виде

Соотношения (2.24) должны выполняться равномерно по

Условия на ребре (2.24) обеспечивают существование интеграла

где V_r - объем кольцевой области радиуса r, охватывающей контур Со. Существо­вание этого интеграла эквивалентно выполнению требования ограниченности энер­гии электромагнитного поля в любом конечном объеме, охватывающем контур С_о (рис.2.3). Анализируя соотношения (2.24) совместно с уравнениями Максвелла,

можно показать, что касательные к ребру (контуру Со) составляющие 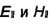долж­ны быть ограниченными, а нормальные к ребру составляющие могут иметь

особенности вида г^-x, где 0<х < 1. Для определения параметра и нужно знать внутренний угол так называемого эквивалентного клина, который строится сле­дующим образом. Через произвольную точку М на рассматриваемом ребре С_о про­водится касательная l к С_о и две полуплоскости, касательные к S в точке М, так, чтобы их ребра совпали с l Клин, образованный этими полуплоскостями, и назы­вают эквивалентным клином (на рис. 2.4 показано сечение поверхности S плоско­стью, перпендикулярной ребру эквивалентного клина в точке М; касательная l пер­пендикулярна плоскости рисунка, а ее след совпадает с точкой М). Пусть внутрен­ний угол эквивалентного клина равен Ω. (предполагается, что Ω< π). Анализируя структуры полей вблизи ребра идеально проводящего клина, найденные на основе

решения соответствующих краевых задач, получили, что x = (π - Ω)/(2π - Ω). В ча­стном случае, когда поверхность S имеет острую кромку (например, на краю беско­нечно тонкого экрана), Ω = 0 и х = 1/2. На таком ребре составляющие имеют

особенность вида const , а составляющие обращаются в нуль как

Из приведенного выше доказательства единственности реше­ния краевых задач электродинамики следует, что при отсутствии потерь энергии в области V решение внутренней задачи может быть неединственным. Физически это означает, что в такой систе­ме помимо полей, созданных непрерывно действующими сторон­ними источниками, могут существовать незатухающие поля, соз­данные когда-то действовавшими сторонними источниками (но в рассматриваемое время переставшими действовать). Эти поля из-за отсутствия потерь в среде могут существовать сколь угодно долго (например, собственные колебания идеального объемного резонатора).