
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Прості задачі комбінаторного типу
|
|
Мирон Маланюк, Василь Кравчук
Метод математичної індукції та елементи комбінаторики
За редакцією Василя Тадеєва
Видання 2-е, виправлене

| ТЕРНОПІЛЬ «ПІДРУЧНИКИ & ПОСІБНИКИ 2003 |
ББК 22.12
УДК 51.1
М 18
Рецензент:
кандидат фізико-математичних наук В. Д. Галан
| М 18 | Маланюк Мирон, Кравчук Василь Метод математичної індукції та елементи комбінаторики. За редакцією В. Тадеєва. Видання 2-е, виправлене. — Тернопіль: Підручники і посібники, 2003. — 48 с. ISBN 966-07-0002-4 |
Посібник входить в систему дидактичних матеріалів для учнів Західноукраїнської заочної математичної школи. В ньому викладено один з основних методів доведення математичних тверджень — метод математичної індукції. На основі цього методу зроблено спробу компактно розглянути основні поняття комбінаторики. Наведено найпоширеніші методи розв’язування комбінаторних задач. Вміщено завдання для двох контрольних робіт за даною темою та добірку задач для самостійної підготовки до математичних олімпіад.
Посібник може бути корисним і для вчителів математики у гуртковій роботі.
ББК 22.12
ISBN 966-07-0002-4
© Маланюк М. П., Кравчук В. Р., 1995
Передмова редактора
«Нам такою мірою ненависний будь-який обман і шахрайство, що всім членам нашого товариства під загрозою штрафу та безчестя заборонено показувати яке б то не було природне явище прикрашеним або перебільшеним: а лише в чистому ви-гляді, без будь-якої таємничості.»
Френсіс Бекон
(англійський філософ ХVП ст.),
«Нова Атлантида»
Професор Отто Ліденброк — головний герой роману «Подорож до центра Землі» — належав до тієї ж когорти жульвернівських лицарів науки, істинних учених і справжніх колодязів знань, що й відоміші тепер Жак Паганель («Діти капітана Гранта»), Сайрес Сміт («Таємничий острів») та доктор Клоубоні («Подорож іпригоди капітана Гаттераса»). Найбільшою пристрастю професора після, звичайно ж, геології був пошук рідкісних книг. Одного разу йому особливо пощастило. В букіністичній крамниці він натрапив на манускрипт (рукописну книгу) ХІІІ ст., написану рунічним письмом (руни — письмові знаки (літери), що вживалися в середньовічній Ісландії і, за легендою, були винайдені самим Одіном — верховним богом в ісландській міфології). Та ще більшою несподіванкою стала записка, залишена у цій книзі її колишнім володарем — знаменитим алхіміком XVI ст. Арне Сакнуссемом. Сумніву не було, що у записці йдеться про велике відкриття. Адже запис здійснено тим самим добре відомим професору рунічним письмом, яким написана й книга. Проте прочитати записку було годі: повідомлення було зашифроване. «Я вважаю безсумнівним, — сказав професор своєму племіннику і помічнику Акселю, — що спочатку відповідна фраза була написана правильно, а потім за якимсь правилом, яке треба знайти, спотворена».
Допомогла випадковість. Обмахуючись спересердя після чергової невдалої спроби аркушем паперу з переведеними на латину записами букв шифрування, Аксель помітив, що читати його слід просто в зворотному напрямку. Арне Сакнуссем повідомляв про свою подорож … до центра Землі через кратер вулкану Снайфельдс в Ісландії, причому через ту з його шахт, до якої в кінці липня сягає тінь від піку Скартарис. Ця вказівка, за Жуль Верном, і дала змогу професору та його помічникам повторити незвичайну подорож великого алхіміка до земних глибин.
Прочитавши, завдячуючи такій випадковості, документ, Аксель з хвилюванням спостерігав за професором, який, охолонувши, знову взявся за роботу і за всяку ціну намагався прочитати шифрування. «Я добре знав, — згадував він потім, — що якби професору вдалося скласти з усіх цих букв усі можливі буквосполучення, то шукана фраза врешті-решт вийшла б. Але я знав також, що з двадцяти букв отримується два квінтильйони, чотириста тридцять два квадрильйони, дев’ятсот два трильйони, вісім мільярдів, сто сімдесят шість мільйонів, шістсот сорок тисяч буквосполучень. А в цьому записі було сто тридцять дві букви, і ці сто тридцять дві букви могли утворити таку неймовірну кількість словосполучень, що не тільки полічити їх було б неможливо, а й уявити собі. Я міг заспокоїтися щодо цього героїчного способу вирішити проблему».
По-справжньому оцінити цей епізод з жюльвернівського роману в змозі лише той, хто знайомий з комбінаторикою — математичною наукою про способи підрахунку числа різноманітних комбінацій з елементів деякої скінченної множини (назва походить від латинського слова «соmbinа», що означає «сполучати», «зв’язувати»). Їй i присвячена більша частина цієї брошури.
Шифрування і дешифрування текстів — одне з першоджерел комбінаторики, а також і сфера її застосувань. Найбільш вражаючі результати від цих застосувань пов’язані з розшифровуванням прадавніх історичних писемних пам’яток, зокрема — ієрогліфічних єгипетських папірусів та клинописних вавилонських табличок. Унаслідок філологічного та комбінаторного аналізу так званих «білінгвів» — паралельних записів різними давніми мовами, наприклад, давньогрецькою і давньоєгипетською — у ХІХ–ХХ ст. «заговорили» прадавні письмена, яких не могли прочитати вже навіть давні греки в епоху розквіту їхньої культури.
З комбінаторикою пов’язані і теперішні задачі цифрованого кодування інформації, наприклад, при створені державних номерних знаків для транспортних засобів, шифрованих товарних знаків тощо. До здійснення цілеспрямованого перебору різних можливих варіантів призводять численні задачі виробничої діяльності, наприклад, прокладання маршрутів, проектування комунікацій, складання розкладу руху транспорту, графіків подачі ресурсів, розкладів занять у навчальних закладах тощо.
Нарешті, джерелом комбінаторики та чи не найширшою тепер сферою її застосувань є теорія ймовірностей.
Усім добре відомо, що різні випадкові події випадкові, образно кажучи, по-різному. Наявність кожного конкретного звука у слові випадкова. Проте одні звуки у мові трапляються частіше, інші — рідше (зокрема, це мають на увазі, коли кажуть про ритмічність мови, про її благозвучність, мелодійність тощо). Отже, ймовірність одних звуків більша, ймовірність інших — менша. Інший приклад. Виграш у кожній лотереї — випадковий. Але в одній лотереї (наприклад, у книжковій) він трапляється значно частіше, отже, ймовірніший, ніж в іншій (наприклад, у спортлото). Щоправда довший час такими речами цікавилися здебільшого тільки запеклі гравці в азартні ігри. І тільки в XX ст., коли було відкрито імовірнісний характер багатьох фундаментальних явищ природи (зокрема, на рівні елементарних частинок), необхідність вивчення міри випадковості, тобто ймовірності різних випадкових подій, стала очевидною.
Початки теорії ймовірностей були закладені у XVII ст., коли декількох найвидатніших математиків того часу спровокували до аналізу азартних ігор, зокрема — гри у кості. Як відомо, ця гра полягає в тому, що декілька однакових кубиків з нанесеними на їхніх гранях очками від 1до 6 по черзі кидаються на стіл кількома гравцями. У найпростішому варіанті гри ставку бере той, кому випала найбільша сумарна кількість очок. Однак при цьому ймовірність виграшу в кожного учасника однакова. Через те найверткіші пройдисвіти, «удосконалюючи» гру, запроваджували такі правила, які на перший погляд були гіршими для них, проте насправді забезпечували їм більшу вірогідність виграшу. Славою великого вигадника таких правил ко-ристувався свого часу якийсь Мере. Одне з його «удосконалень», погоджене із самим Блезом Паскалем, було таким: щоразу кидаються чотири кісточки, а виграш бере Мере лише в тому разі, коли хоча б на одній з кісточок випаде шістка. Таке «невинне» удосконалення призвело до того, що Мере частіше вигравав, ніж програвав. Прочитавши цю брошуру, читач зрозуміє, в чому причина. А вона полягає в тому, що при киданні чотирьох кісточок усього можливо 6 · 6 · 6 · 6 = 1296різних варіантів випадання очок. Шістка жодного разу не з’явиться у 5 · 5 · 5 · 5 = 625 випадках, а отже, з’явиться хоча б один раз у 64 – 54 = 671 випадку. Таким чином, ймовірність  того, що шістка з’явиться хоча б один раз, більша за ймовірність
того, що шістка з’явиться хоча б один раз, більша за ймовірність  того, що вона не з’явиться жодного разу. Різниця незначна. Але при багаторазових сеансах гри вона може забезпечити значний виграш.
того, що вона не з’явиться жодного разу. Різниця незначна. Але при багаторазових сеансах гри вона може забезпечити значний виграш.
В загальному випадку якщо стан якогось об’єкта чи системи може характеризуватися одним з п однаково можливих характерних станів визначальних елементів, а деякій випадковій події А, пов’язаній з цим об'єктом, сприяє т (  ) із цих станів, то кажуть, що ймовірність події А дорівнює
) із цих станів, то кажуть, що ймовірність події А дорівнює  .
.
Як бачимо, підрахунок імовірностей безпосередньо пов’язаний з підрахунком кількості комбінацій, а отже, з відповідною комбінаторною проблематикою. У цій брошурі, однак, глибше ці зв’язки не простежуються. Але читач, який ґрунтовно ознайомиться з наведеним тут матеріалом, без особливих зусиль зможе розв’язувати і ймовірнісні задачі, наприклад, визначати шанси виграшу у лотерею Спортлото (і після цього перестати грати в такі ігри).
Своїй назві комбінаторика завдячує видатному вченому, математику та філософу Ґотфріду Вільгельму Лейбніцу. У 1646 р. у двадцятирічному віці він опублікував твір під назвою «Dissertatio de art combinatoria» (що в перекладі з латини означає «Міркування про комбінаторне мистецтво»), в якому заклав основи цієї теорії.
Чи не найсуттєвішою проблемою при ознайомленні з комбінаторикою є чітке розмежування основних понять і символів для їх позначення. Звикнутись із символами буде простіше, якщо зважити, що вони безпосередньо пов’язані з англійськими назвами відповідних термінів: С — від «Combination» («комбінація»), Р — від «Permutation» («перестановка»), А —від «Arrangement» («розміщення»).
Основні факти комбінаторики виражаються у вигляді формул для обчислення кількості певним чином утворених підмножин з елементів деякої скінченної множини — перестановок, комбінацій, розміщень тощо. Універсальним методом для доведення цих формул, який застосовують і в інших розділах математики — всюди, де тільки виникає потреба доведення тверджень, що залежать від натурального параметра, — є так званий метод математичної індукції. У неявній формі цей метод застосовувався ще античними математиками, зокрема Евклідом. Проте систематичне і явне застосування даного методу розпочалося у XVII ст. Зокрема, ним широко користувався Блез Паскаль у своїй праці з комбінаторики. Сам термін «математична індукція» вперше з’явився у 1838р. в Британській Енциклопедії (відповідну статтю про цей метод написав відомий шотландський математик, перший президент Лондонського математичного товариства Августус де Морган (1806 – 1871).
Зрозуміти глибинну суть методу математичної індукції читачу допоможе наступне порівняння (математики кажуть, — аналогія). Вам відомий спосіб задання числових послідовностей за допомогою так званих рекурентних формул («recurro» в перекладі з латини означає «біжу назад», «повертаюсь»), за якими n-й член послідовності виражається через попередні, а в найпростішому випадку — лише через один (п – 1)-й член. Такими є, наприклад, наступні формули для членів арифметичної та геометричної прогресій, що безпосередньо випливають з означень цих послідовностей:  ;
;  (тут
(тут  і
і  — відповідно, різниця арифметичної та знаменник геометричної прогресій). Отже, знаючи перший член а1 прогресії, наприклад арифметичної, ми за рекурентною формулою можемо спочатку обчислити другий її член
— відповідно, різниця арифметичної та знаменник геометричної прогресій). Отже, знаючи перший член а1 прогресії, наприклад арифметичної, ми за рекурентною формулою можемо спочатку обчислити другий її член 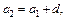 потім третій a3 = a2 + d, і так далі, нарешті, обчисливши (п – 1)-й член, знайти n-й член прогресії.
потім третій a3 = a2 + d, і так далі, нарешті, обчисливши (п – 1)-й член, знайти n-й член прогресії.
Методом математичної індукції по суті встановлюється рекурентна форма для доведення (induktio — дослівно «наведення», — також вказує на це). Адже при доведенні цим методом твердження, залежного від натурального параметра n, по-перше, встановлюється істинність цього твердження при п = 1 (аналог першого члена  у рекурентній формулі для задання послідовності). Це так звана база індукції. Потім, припустивши, що твердження доведене при
у рекурентній формулі для задання послідовності). Це так звана база індукції. Потім, припустивши, що твердження доведене при  (аналог члена
(аналог члена  у рекурентній формулі — припу-щення індукції), показують, що воно буде істинним і при
у рекурентній формулі — припу-щення індукції), показують, що воно буде істинним і при  (це крок індукції і, власне, аналог самої рекурентної формули для послідовності). Тоді твердження буде доведеним для всіх п. Справді, розпочинаючи з твердження при
(це крок індукції і, власне, аналог самої рекурентної формули для послідовності). Тоді твердження буде доведеним для всіх п. Справді, розпочинаючи з твердження при  доведеного як базового для індукції, ми, як при обчисленні на-ступних членів прогресії за рекурентною формулою, матимемо, згідно з проведеним кроком індукції, істинність даного твердження при п = 1 + 1 = 2, потім — при п = 2 + 1 = 3, і так далі, тобто — при всіх n.
доведеного як базового для індукції, ми, як при обчисленні на-ступних членів прогресії за рекурентною формулою, матимемо, згідно з проведеним кроком індукції, істинність даного твердження при п = 1 + 1 = 2, потім — при п = 2 + 1 = 3, і так далі, тобто — при всіх n.
На завершення зазначимо, що свого часу елементи комбінаторики та метод математичної індукції входили до програми з математики для середньої школи. І лише у зв’язку із скороченням часу на вивчення математики ці теми були перенесені на факультативи та на самостійне опрацювання. Але тепер вони знову вводяться до шкільного викладання. Отже, цей матеріал цілком доступний для учнів. Тим більше для тих, хто додатково цікавиться математикою.
У посібнику використовуються такі умовні позначення:
початок і кінець розв’язання задачі та доведення теореми відзнача-ється значком ■;
запис  означає, що ціле число а ділиться на ціле число b (без остачі);
означає, що ціле число а ділиться на ціле число b (без остачі);
при  символом
символом  позначається добуток
позначається добуток  усіх натуральних чисел від 1до n. Вважається, також, що
усіх натуральних чисел від 1до n. Вважається, також, що 
В. О. Тадеєв
Метод математичної індукції
Розглянемо дві задачі.
Задача 1.Довести, що вираз  при всіх дійсних а набуває додатних значень.
при всіх дійсних а набуває додатних значень.
Розглянемо такі випадки.
1) При  очевидно, що
очевидно, що  .
.
2) При 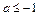 маємо:
маємо:  ,
,  , а тому
, а тому 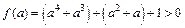 .
.
3) При –1 < а < 0запишемо заданий вираз у вигляді: 
 Оскільки
Оскільки  і при –1 < а < 0 маємо:
і при –1 < а < 0 маємо: 
 то
то  . Отже,
. Отже,  при всіх
при всіх  .
.
Задача 2.Знайти суму перших n непарних натуральних чисел.
Розглянемо окремі випадки:
При n = 1: 1 = 12.
При n = 2: 1 + 3 = 22.
При n = 3: 1 + 3 + 5 = 9 = 32.
При n = 4: 1 + 3 + 5 + 7 = 16 = 42.
Після розгляду цих випадків напрошується висновок, що сума перших n непарних натуральних чисел дорівнює n2.
В обох розглянутих задачах загальні висновки: «  при всіх
при всіх  » та «сума перших n непарних натуральних чисел дорівнює n2» ми зробили на основі розгляду часткових випадків. Загальні висновки, зроблені на основі розгляду часткових випадків, якщо ці висновки полягають у поширенні помічених закономірностей на загальний випадок, називають індуктивними, а сам метод таких міркувань називають індуктивним методом, або індукцією.
» та «сума перших n непарних натуральних чисел дорівнює n2» ми зробили на основі розгляду часткових випадків. Загальні висновки, зроблені на основі розгляду часткових випадків, якщо ці висновки полягають у поширенні помічених закономірностей на загальний випадок, називають індуктивними, а сам метод таких міркувань називають індуктивним методом, або індукцією.
Якщо загальний висновок робиться на основі розгляду всіх можливих випадків, то такий метод міркувань називають повною індукцією. Наприклад, задача 1розв’язана методом повної індукції. З цим методом доведення ви вже зустрічалися раніше. Зокрема, доведення теореми про величину вписаного в коло кута зводиться до розгляду трьох випадків — залежно від розміщення центра кола відносно сторін вписаного кута.
Якщо загальний висновок робиться на основі розгляду лише окремих можливих випадків, то такий метод міркувань називають неповною індукцією. Загальний висновок в задачі 2виведений на основі неповної індукції.
Зауважимо, що, строго кажучи, задача 2нами ще не розв’язана. Розглянувши декілька випадків, ми не можемо гарантувати, що зроблений загальний висновок правильний для всіх натуральних n. Тому поки що цей висновок будемо називати гіпотезою, а правильність цієї гіпотези доведемо пізніше.
Зазначимо, що індуктивні міркування можуть привести і до помилкових висновків. Підтвердимо це прикладом. Розглянемо квадратний тричлен  Підставляючи замість х значення 1, 2, 3, 4, 5, 6, дістанемо відповідні значення цього тричлена: 41, 43, 47, 53, 61, 71. Неважко помітити, що всі ці числа є простими. Використовуючи метод неповної індукції, можна було б дійти висновку, що значення даного тричлена для натуральних х завжди будуть простими числами. У правильності такого висновку нібито переконують нас і подальші обчислення (див. таблицю):
Підставляючи замість х значення 1, 2, 3, 4, 5, 6, дістанемо відповідні значення цього тричлена: 41, 43, 47, 53, 61, 71. Неважко помітити, що всі ці числа є простими. Використовуючи метод неповної індукції, можна було б дійти висновку, що значення даного тричлена для натуральних х завжди будуть простими числами. У правильності такого висновку нібито переконують нас і подальші обчислення (див. таблицю):
| x | |||||||||||
| х2 – х + 41 | . |
Всі виписані тут значення квадратного тричлена знову-таки є простими числами. Більше того, аналогічні результати одержуються для всіх наступних натуральних значень х аж до числа х = 40. Однак при х = 41число  = 412уже не є простим. Отже, індуктивний висновок про те, що всі значення тричлена
= 412уже не є простим. Отже, індуктивний висновок про те, що всі значення тричлена  для натуральних х завжди є простими числами, — хибний.
для натуральних х завжди є простими числами, — хибний.
Таким чином, неповна індукція не є повноцінним методом математичного доведення. Водночас припущення, зроблені на основі такої індукції, широко використовуються як робочі гіпотези, що потребують, однак, строго логічного доведення. Один з методів для доведення таких гіпотез дістав назву методу математичної індукції.
Метод математичної індукції називають ще методом повної математичної індукції. Використовується він при доведенні тверджень, які залежать від натурального числа. Прикладами таких тверджень є:
— для будь-якого натурального п виконується рівність
1 + 2 +…+ n = 
— при будь-якому натуральному п число 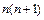 ділиться на 2;та ін.
ділиться на 2;та ін.
В основі методу математичної індукції лежить такий принцип.
Принцип математичної індукції. Якщо деяке твердження істинне для п = 1і з істинності цього твердження для якого-небудь довільного натурального n = k випливає його істинність для n = k + 1, то дане твердження істинне для будь-якого натурального числа n.
Правомірність застосування цього принципу не викликає сумніву. Адже ним на основі істинності твердження при п =1гарантується істинність цього твердження при п =1 + 1 = 2,далі на основі істинності при п = 2 —істинність при п = 2 + 1= 3і т. д., отже — істинність при всіх натуральних n.
Доведення тверджень методом математичної індукції складається з двох етапів, або кроків: перевірки бази індукції та здійснення індуктивного переходу.
1. База індукції. Доводять, що твердження істинне для п =1.
2. Індуктивний перехід. Припускають, що твердження істинне для n = k і, використовуючи це припущення, доводять істинність твердження для п = k + 1.
Якщо обидва ці кроки доведення виконані, то на основі принципу математичної індукції, твердження є істинним для довільного натурального числа п.
Використовуючи метод математичної індукції, завершимо розв’язування задачі 2,тобто доведемо рівність:
 . (1)
. (1)
■ 1. При п =1у лівій частині рівності (1)буде лише один доданок 1, а права її частина дорівнюватиме 12 = 1. Отже, при п = 1рівність (1)правильна.
2. Припустимо, що рівність (1)єправильною при n = k, тобто, що  , і доведемо, що тоді рівність (1)правильна і при n = k + 1, тобто що
, і доведемо, що тоді рівність (1)правильна і при n = k + 1, тобто що 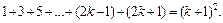
Використовуючи припущення  матимемо:
матимемо:


Отже, за принципом математичної індукції, рівність (1)єправильною для довільного натурального числа n. ■
Розглянемо ще декілька прикладів.
Приклад 1.Вивести формулу для добутку  .
.
■ Позначимо цей добуток через 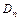 . Тоді
. Тоді 
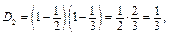

Кожне із записаних значень добутку Dn є дробом, чисельник якого 1, а знаменник на одиницю більший від номера n цього добутку. Тому можна припустити, що
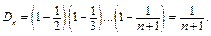 (2)
(2)
Доведемо правильність рівності (2)методом математичної індукції.
1. Правильність рівності (2)при n =1 вже встановлено.
2. Припустимо, що рівність (2)правильна при n = k, тобто що

Покажемо тоді, що  Маємо:
Маємо:


Отже, рівність (2) єправильною для довільного натурального числа n. ■
Приклад 2. Довести нерівність Бернуллі (Якоб Бернуллі (1654 –1705) —швейцарський математик):
 де
де  (3)
(3)
■ 1. При п = 1маємо:  що є правильним.
що є правильним.
2. Припустимо, що є правильною нерівність  , і покажемо, що тоді правильною є й нерівність
, і покажемо, що тоді правильною є й нерівність  . Справді,
. Справді,

(оскільки  ).
).
Отже, нерівність (3)правильна для всіх натуральних n. ■
Приклад 3. Довести нерівність: 
■ 1. При n = 1 дана нерівність є правильною, оскільки 
2. Припустимо, що ця нерівність виконується при n = k, тобто що

Покажемо, що в такому разі ця нерівність буде виконуватися і при n = k + 1, тобто що

Матимемо: 

Отже, задана нерівність є правильною при довільному натуральному n. ■
Зауваження. Є твердження, які істинні не для всіх натуральних чисел, а для натуральних чисел, починаючи з деякого числа m. Наприклад, нерівність  справджується для натуральних
справджується для натуральних 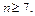 Є також твердження, які істинні не тільки для натуральних, а й для цілих значень n, починаючи з деякого цілого від’ємного числа або з нуля. Наприклад, нерівність Бернуллі істинна і при n = 0. При доведенні таких тверджень спираються на таке узагальнення принципу математичної індукції:
Є також твердження, які істинні не тільки для натуральних, а й для цілих значень n, починаючи з деякого цілого від’ємного числа або з нуля. Наприклад, нерівність Бернуллі істинна і при n = 0. При доведенні таких тверджень спираються на таке узагальнення принципу математичної індукції:
Якщо твердження істинне для n = m, де m — деяке ціле число, і з істинності твердження для довільного цілого n = k (k  m) випливає його істинність для n = k + 1, то це твердження істинне для будь-якого цілого
m) випливає його істинність для n = k + 1, то це твердження істинне для будь-якого цілого 
Зрозуміло, що встановлення бази індукції у цьому разі зводитиметься до доведення істинності твердження при n = m.
Приклад 4. Довести, що  при всіх цілих
при всіх цілих 
■ Позначимо вираз  через
через  .
.
1. При n = –1  Оскільки
Оскільки  то
то  при n = –1.
при n = –1.
2. Припустимо, що  , де
, де 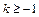 — ціле число, і покажемо, що тоді
— ціле число, і покажемо, що тоді  .
.
Справді, 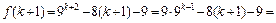

Кожний із доданків останнього виразу ділиться на 16 (перший — за припущенням). Отже,  при будь-якому цілому
при будь-якому цілому  . ■
. ■
Неакуратність у застосуванні методу математичної індукції може стати джерелом хибного твердження. Про це свідчить такий жарт.
«Доведемо» методом математичної індукції твердження: «Всі на світі коти — чорні». Один чорний кіт існує, — це очевидно. Припустимо, що будь-які k котів є чорними. Візьмемо деяких k + 1 котів і заховаємо їх у мішок. Якщо з мішка витягнути одного кота, то в мішку залишиться k котів, які за припущенням є чорними. Витягнемо з мішка ще одного кота (зрозуміло, що він — чорний), а в мішок заховаємо першого кота. Тоді в мішку знову буде k котів, які за припущенням є чорними. Заховуємо другого витягнутого кота в мішок. У ньому вже всі k + 1 котів будуть чорними. Отже, за принципом математичної індукції, усі на світі коти — чорні.
Неправомірність цих міркувань полягає в тому, що не було перевірено істинності відповідного твердження при n = 1, адже висловлення «Будь-який один кіт є чорним» — хибне.
Прості задачі комбінаторного типу
З комбінаторними задачами читачі зазвичай стикаються задовго до того, як розпочинають систематично вивчати цей розділ математики. Такі задачі зустрічаються і в шкільних підручниках та посібниках для позакласних занять. Розглянемо деякі найпростіші задачі такого типу.
Задача 1. Є 6 замків і 6 ключів до них. Кожний ключ підходить лише до одного замка. Вставляючи ключ у замок, можна з’ясувати, підходить він до цього замка чи ні. Скільки таких перевірок потрібно провести, аби підібрати ключі до усіх замків?
■ Очевидно, що за допомогою не більше як п’ятьох перевірок визначиться ключ до першого замка. Після цього не більше як чотирма випробуваннями визначиться ключ до другого замка. Потім відповідно не більше як 3 і 2 випробування дадуть змогу з’ясувати, які ключі підходять до третього і четвертого замків. Нарешті, достатньо лише одного випробування, аби підібрати ключ до п’ятого замка. Ключ, який залишиться, мусить підходити для останнього замка. Тому усього потрібно буде не більше, ніж 5 + 4 + 3 + 2 + 1 = 15 перевірок, аби підібрати ключі до усіх замків. А найменша можлива кількість перевірок — 5. ■
Задача 2. Скільки існує чотирицифрових чисел, які можна записати:
а) тільки непарними цифрами;
б) тільки парними цифрами;
в) цифрами різної парності?
■ а) Мова йде лише про числа вигляду 3715, 9171, 3373 та ін. Оскільки непарних цифр є 5, то першу цифру можна вибрати п’ятьма способами. Це саме можна сказати й про інші цифри. Тому шуканих чотирицифрових чисел існує 5·5·5·5 = 625.
б) Оскільки перша цифра не може бути нулем, то її можна вибрати лише серед цифр 2, 4, 6 і 8. Кожну з інших цифр можна вибрати п’ятьма способами. Тому чотирицифрових чисел, записаних лише парними цифрами, існує 4·5·5·5 = 500.
в) Усіх чотирицифрових чисел є 9·10·10·10 = 9000. Якщо ми відкинемо ті з них, які записуються тільки непарними або тільки парними цифрами, то дістанемо чотирицифрові числа, у записі яких містяться і парні, і непарні цифри. Отже, таких чисел існує 9000 – (625 + 500) = 7875. ■
Задача 3. Скільки існує натуральних чисел, менших від 100, які:
а) діляться на 2;
б) не діляться на 2;
в) діляться на 3;
г) діляться одночасно і на 2, і на 3;
ґ) діляться на 2, але не діляться на 3;
д) діляться на 3, але не діляться на 2;
е) діляться або на 2, або на 3;
є) не діляться ні на 2, ні на 3?
■ При відшуканні відповідей на ці запитання можна було б виписати всі натуральні числа від 1 до 99 і полічити, скільки серед них таких, які нас цікавлять. А можна відшукати закономірності, яким підпорядковані числа кожного з указаних видів. Наприклад, на 2 діляться лише парні натуральні числа 2, 4, 6, ..., 98. Їх, очевидно, — 49. Це число можна дістати як цілу частину від дробу  (адже натуральних чисел, менших від 100, є 99, а на 2 ділиться кожне друге натуральне число). Цілу частину числа позначають за допомогою квадратних дужок, наприклад:
(адже натуральних чисел, менших від 100, є 99, а на 2 ділиться кожне друге натуральне число). Цілу частину числа позначають за допомогою квадратних дужок, наприклад:  .
.
Відповідь на запитання б) з’ясовується просто. Чисел, які не діляться на 2, є 99 – 49 = 50.
На 3 ділиться кожне третє число із послідовності перших 99 натуральних чисел, а саме: 3, 6, 9,..., 96, 99. Їх існує  .
.
Аби відповісти на запитання г), можна було б відшукати, скільки натуральних чисел, менших від 100, ділиться на 6. Їх існує  . Відповідь можна знайти й так: з послідовності чисел 3, 6, 9, 12, ..., 96, 99, кратних 3, вибрати лише парні числа; їх є
. Відповідь можна знайти й так: з послідовності чисел 3, 6, 9, 12, ..., 96, 99, кратних 3, вибрати лише парні числа; їх є  Відповідь на це запитання дістали б, якби обчислили
Відповідь на це запитання дістали б, якби обчислили  Подумайте і поясніть чому.
Подумайте і поясніть чому.
Натуральних чисел, які менші від 100, діляться на 2, але не діляться на 3, є 49 – 16 = 33. Чисел, які діляться на 3, але не діляться на 2, є 33 – 16 = 17.
Очевидно, що натуральних чисел, які не перевищують 99 і діляться на 2 або на 3, є 49 + 33 – 16 = 66. Відповіддю на запитання є) буде: 99 – 66 = 33. ■
Зрозуміло, що можна розглядати й інші аналогічні запитання. Наприк-лад: скільки існує натуральних чисел, які не перевищують 1000 і не діляться ні на 5, ні на 6, ані на 7. Поясніть, чому відповіддю на таке запитання є:
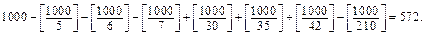
Задача 4. Скільки існує двоцифрових чисел, менших від 100, цифри яких:
а) розміщені в порядку зростання (тобто перша цифра менша від другої);
б) у порядку спадання;
в) у не зростаючому порядку (перша цифра більша або дорівнює другій)?
■ а) У першому десятку таких чисел немає, у другому їх 8, бо числа 10 та 11 потрібної властивості не мають. І так далі. Усіх двоцифрових натуральних чисел, які не перевищують 100 і в записі яких цифри розміщені в порядку зростання, є 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 36.
б) У порядку спадання цифри розміщені у числах 10, 20, 21, 30, 31, 32 і т. д. Якщо міркувати так само, як і в першому випадку, то знайдемо 45 двоцифрових чисел, цифри яких розміщені у порядку спадання.
в) Є 9 двоцифрових чисел 11, 22, 33, 44, 55, 66, 77, 88, 99, цифри яких рівні між собою. Про ці числа можна сказати, що їхні цифри розміщені у не зростаючому (або, якщо потрібно, — у не спадному) порядку. Тому чисел, цифри яких розміщені у не зростаючому порядку, існує 45 + 9 = 54. ■
Задача 5. Є чотири кульки однакових розмірів, але різної маси. За допомогою скількох зважувань на шалькових терезах без важків можна розмістити ці кульки в порядку спадання їхніх мас?
■ Очевидно, що кожне зважування двох кульок дає змогу визначити, яка з них має більшу, а яка меншу масу.
Два зважування дають змогу виділити у двох парах важчі і легші кульки. Третє зважування визначає серед двох важчих кульок найважчу, а четверте серед двох легших — найлегшу. Знаючи серед чотирьох кульок найважчу і найлегшу, за допомогою п’ятого зважування упорядкуємо маси двох кульок, що залишилися. ■
Задача 6. Шість студентів, присутніх у кімнаті, знають англійську мову, стільки ж — німецьку, і сім студентів знають французьку мову. Один із цих студентів знає всі три згадані мови, чотири студенти знають німецьку та англійську, два — французьку та англійську, а три — німецьку та французьку мови. Скільки усіх присутніх у кімнаті, якщо кожен з них знає хоча б одну зі згаданих мов?
■ При розв’язуванні цієї задачі доцільно скористатися табличним записом.
Якби з кімнати вийшов той студент, який знає усі три мови, то дістали б ситуацію, яка описується другим рядком таблиці. Якби вийшли ті студенти, які знають по дві іноземні мови, ситуація відображалася б третім рядком. Тоді в кімнаті залишилося б лише 4 студенти. Оскільки вийшло 7 студентів, то шукана відповідь — 11. ■
| а | н | ф | ан | аф | нф | анф | |
| Спочатку | |||||||
| Після першого виходу | |||||||
| Після другого виходу |
Задача 7. (Жартівлива задача Льюїса Керролла.) У жорстокому бою 70 зі 100 піратів втратили по оку, 75 втратили вухо, 80 були поранені в руку і 85 — в ногу. Яка мінімальна кількість тих, хто зазнав одночасно всіх чотирьох поранень, тобто був поранений в око, вухо, руку і в ногу?
■ Якби усі 30 піратів, що зберегли свої очі, були поранені у вухо, то 45 були б поранені двічі (в око і у вухо). Отже, було б лише 55 піратів з одним пораненням в око або у вухо. Коли б усі ці 55 піратів були поранені в руку, то було б лише 25 піратів, які дістали три поранення (в око, вухо і в руку), і 75 мали б лише два поранення. Коли б усі ці 75 піратів були поранені в ногу, то ще 10 чоловік мали б четверте поранення. Це і є мінімальна кількість людей, які могли б дістати усі чотири поранення. Зрозуміло, що максимальною кількістю потерпілих, які могли б дістати усі 4 поранення, є 70.■
Аналогічні задачі, які підводять до усвідомлення комбінаторних закономірностей, можна зустріти у багатьох посібниках, зокрема у книзі М. П. Маланюка та В. І. Лукавецького «Олімпіади юних математиків», виданій у Києві видавництвом «Радянська школа» в І977 році (ст. 37–40).
|
Просмотров 979 |
|
|
