Сполуки з повторенням елементів

Розглядаючи задачу про те, скільки різних буквосполучень можна дістати, переставляючи букви слова ранок, легко отримати відповідь: їх буде Р₅ = 120. Якщо аналогічне запитання поставити стосовно слова математика, то ситуація зміниться, бо в цьому слові буква а зустрічається 3 рази, і по два рази зустрічаються букви м і т. Для проведення підрахунку різних буквосполучень у цьому разі, уявімо собі, що всі букви даного слова різні за написом. Нехай, наприклад, букви, що повторюються, записані з індексами: м₁а₁т₁е₁м₂а₂т₂ика₃. Тоді кількість можливих буквосполучень, одержаних перестановкою усіх цих букв, дорівнюватиме 10!. Серед них для кожного конкретного розміщення букв м₁, м₂, т₁, т₂, е, и, к матимемо по 3! = 6 таких буквосполучень, у яких міняються місцями лише букви a₁, а₂, а₃. Зрозуміло, що в традиційному написанні (без індексів) ці буквосполучення тотожні між собою. Так само, для кожного конкретного розміщення букв а₁, а₂, а₃, т₁, т₂, е, и, к матимемо по 2! = 2 буквосполучення, у яких міняються місцями лише букви м₁ і м₂. Аналогічний висновок справджується і стосовно букв т₂, т₁. Тому, згідно з правилом множення, при кожному фіксованому розміщенні букв е, и, к матимемо по 3! × 2! × 2! буквосполучень, які відрізняються між собою лише відповідною перестановкою букв а₁, а₂, а₃; т₁, т₂; м₁, м₂ і які, отже, ідентичні у традиційному написанні. Отже, якщо через Р позначимо кількість усіх насправді різних перестановок букв у слові математика, то, згідно з тим самим правилом множення, матимемо: Р × (3! × 2! × 2!) = 10!. Звідси

Перестановки з повтореннями

Нехай маємо множину, яка складається з елементів a, b, c, d,…, l. Перестановки, в яких елемент a повторюється a разів, елемент b повторюється b разів, елементи с і d — відповідно g і d разів, і т. д., а останній елемент l повторюється l разів, називають перестановками з повтореннями. Кількість усіх можливих таких перестановок позначають символом Наприклад, перестановками з повтореннями, у яких елемент а повторюється 2 рази, а елемент b — 3 рази, є

ааbbb аbаbb аbbаb аbbbа bааbb

bаbаb bаbbа bbааb bbаbа bbbаа.

Таких перестановок є 10. Тому = 10.

Справджується така теорема.

Теорема 4. Кількість різних перестановок з повтореннями, у яких елементи а, b, c, d, …, l повторюються відповідно a, b, g, d, …, l разів, визначається формулою:

Доведення цієї теореми неважко провести, узагальнюючи спосіб розв’я­зування попередньої задачі, пов’язаної зі словом математика. Зробіть це самостійно.

Задача. Скільки шестицифрових чисел можна записати, користуючись цифрами 1, 2, 3, якщо у кожному з чисел цифра 1 повинна повторюватися 2 рази, цифра 2 — 3 рази, цифра 3 — 1 раз?

■ Шукана кількість шестицифрових чисел дорівнює ■

Комбінації з повтореннями

Розв’яжемо таку задачу. У крамниці продаються листівки. До послуг покупців є 15 різних видів листівок. Студентці потрібно привітати зі святом своїх рідних і друзів, а для цього необхідно придбати 12 листівок. Звичайно, можна закупити всі 12 однакових листівок, можна також придбати по декілька однакових листівок, а можна закупити і всі різні листівки. Скільки існує різних способів здійснення такої покупки?

■ Позначимо кількість цих способів символом Для спрощення міркувань кожній конкретній можливості здійснення покупки поставимо у відповідність 14 вертикальних рисок (умовних перегородок між наборами одна­кових листівок) і 12 знаків + за таким правилом. Перед першою рискою запишемо стільки знаків +, скільки листівок першого виду виявилося у покупці. Між першою і другою рисками — стільки знаків + , скільки було куплено листівок другого виду. І так далі, нарешті, після 14-ї риски відповідною кількістю знаків + позначимо кількість куплених листівок останнього 15-го виду. Якщо яких-небудь листівок не вибрали зовсім, то між відповідними рисками не ставитимемо нічого. Наприклад, покупці з п’яти листівок 2-го виду та семи листівок 5-го виду відповідатиме символ ï+++++ êêê+++++++ êêêêêêêêêê. Очевидно, що й навпаки, будь-якій такій послідовності з 14 рисок та 12 знаків + відповідатиме певна можлива схема покупки листівок. Для розв’язання задачі, отже, необхідно з’ясувати, скількома способами можна утворити описані символи, у яких вертикальні риски повторюються 14 разів, а знаки + — 12 разів. Очевидно, що кількість таких способів дорівнює ■

Узагальнимо тепер спосіб розв’язування цієї задачі. Припустимо, що нам задано набір з n різних елементів. З’ясуємо, скількома способами можна підібрати k елементів, кожний із яких є одним з елементів заданого набору. Такі множини називають комбінаціями з повтореннями із даних n елементів по k елементів, а їхню кількість позначають символом Наприклад, комбінаціями з повтореннями із двох елементів а і b по три елементи є: ааа, ааb, аbb, bbb. Отже, Зрозуміло, що при усі 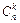комбінацій без повторень входять до складу комбінацій з повтореннями

Сформулюємо таку теорему:

Теорема 5.Кількість різних комбінацій з повтореннями із n елементів по k визначається формулою:

■ Аби порахувати кількість комбінацій з повтореннями із n елементів а₁, а₂, …, а_n по k, встановимо таку взаємно-однозначну відповідність. Кожній конкретній комбінації з повтореннями із елементів а₁, а₂, …, а_n по k поставимо у відповідність послідовність із n – 1 нуля та k одиниць таким чином, щоб: перед першим нулем стояло стільки одиниць, скільки разів у даній комбінації зустрічається елемент а₁; між першим і другим нулями впишемо стільки одиниць, скільки разів зустрічається елемент а₂; між другим і третім нулями впишемо стільки одиниць, скільки разів зустрічається елемент а₃, і т. д. Після останнього (n – 1)-го нуля запишемо стільки одиниць, скільки разів зустрічається елемент а_n (якщо якийсь елемент не зустрічається зовсім, то на відповідному йому місці не записуємо нічого). Кількість таких послідовностей виражається числом що дорівнює кількості перестановок з повтореннями, у яких 1 повторюється k разів, а 0 — п – 1 разів. Отже, ■

Задача. Скількома способами можна розподілити 30 зошитів між чотирма учнями?

■ Нехай при деякому розподілі першому учневі дісталося n₁, другому — n₂, третьому — n₃ а четвертому — n₄ зошитів. Цей розподіл можна схематично зобразити так:

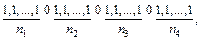
де n₁ + n₂ + n₃ + n₄ = 30. Тепер очевидно, що кількість можливих розподілів дорівнює кількості комбінацій з повтореннями із 4 елементів по 30, тобто числу ■

Розміщення з повтореннями

Розглянемо число 714343733. У його записі цифра 1 зустрічається лише 1 раз, цифра 3 використана 4 рази, цифра 4 повторюється 2 рази, стільки ж разів використана цифра 7. У числі 66666 всі п’ять цифр однакові. Дані два чис­ла є прикладами розміщень з повтореннями. Нижче виписані всі розміщення з повтореннями по 4 символи у кожному, утворені з двох букв а і б; усіх їх 16:

Нехай дано п різних елементів а, b, c, ..., l. Утворимо всі можливі упорядковані множини, кожна з яких містить k елементів. У них деякі елементи можуть повторюватися два, три, ..., k разів. Такі упорядковані множини нази­вають розміщеннями з повтореннями із n елементів, взятих по k. Інакше кажучи, маємо таке означення.

Означення. Розміщеннями з повтореннями з даних п елементів, взятих по k, називаються такі упорядковані множини, які містять по k елементів, кожний з яких є одним з елементів даної n-елементної множини.

Теорема 6. Кількість різних розміщень з повтореннями із п елементів по k дорівнює n^k.

■ Для доведення скористаємось правилом множення. Перший елемент розміщення з повтореннями можна вибрати n способами. Такою ж кількістю способів можна вибрати й другий елемент. Тому перші два елементи разом можна вибрати n² способами. Аналогічно, третій елемент теж можна вибрати n способами, і т. д. Останній k-й елемент так само можна вибрати n способами, адже елементи можуть повторюватися. Отже, за правилом множення, шукана кількість розміщень дорівнює n^k. ■

Доведення цієї теореми можна провести і за допомогою методу математичної індукції. Подумайте самостійно, як це зробити.

Задача. Скільки різних трицифрових чисел можна записати за допомогою цифр 1, 2, 3, 4, 5, 6, якщо цифри можуть повторюватися? Скільки таких чисел можна записати, використовуючи цифри 0, 1, 2, 3, 4, 5?

■ У першому разі шукане число дорівнює кількості розміщень з повтореннями із 6 елементів по 3, тобто 6³ = 216. У другому разі від цього числа слід відкинути кількість записів, у яких на першому місці стоїть цифра 0, наприклад 012, 003, 000. Кількість таких записів дорівнює кількості розміщень з повтореннями із 6 елементів 0, 1, 2, 3, 4, 5 по 2, тобто 6² = 36. Отже, у другому разі шукане число дорівнює 216 – 36 = 180. ■