Потенциальные векторные поля

Пусть - непрерывное векторное поле, определенное в некоторой области пространства . Говорят, что векторное поле 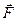потенциально в рассматриваемой области, если существует скалярное поле , градиент которого равен . Таким образом, сказанное означает, что

, . (3.5)

Скалярное поле , для которого справедливо равенство (3.5) называется потенциалом векторного поля .

Пусть в пространстве задана декартова система координат . Тогда, проецируя (3.5) на координатные оси, приходим к равенствам:

, , . (3.6)

Если координаты векторного поля непрерывно дифференцируемы, то, дифференцируя равенства (3.6) по подходящим переменным и пользуясь теоремой о смешанных производных, легко получить следующие, необходимые условия потенциальности векторного поля:

, , . (3.7)

Вспомнив формулу (2.13), выражающую матрицу производной векторного поля в декартовых координатах, можно сделать вывод, что необходимым условием потенциальности дифференцируемого векторного поля является симметричность его матрицы производной.

Пусть векторное поле потенциально в области , - его потенциал (так что ), а - некоторый гладкий (или кусочно-гладкий) путь, лежащий в области , имеющий параметрическое уравнение , .

Вычислим интеграл . Применяя формулу (3.4) и учитывая, что , получим

.

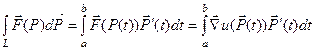Согласно формуле (1.19),

.

Следовательно, справедливо равенство

. (3.8)

Равенство (3.8) показывает, что линейный интеграл в потенциальном векторном поле не зависит от формы пути, а зависит лишь от его начала и конца и равен разности потенциалов в конце и начале пути.

Оказывается, что свойство интеграла в векторном поле не зависеть от формы пути является не только необходимым, но и достаточным условиям потенциальности этого векторного поля. Другими словами, справедлива следующая

Теорема 3.1. Векторное поле , потенциально тогда и только тогда, когда линейный интеграл в этом поле не зависит от формы пути.

Докажем, что условие независимости линейного интеграла в векторном поле от формы пути является достаточным для его потенциальности. Необходимость этого условия выражается равенством (3.8). Пусть - некоторая фиксированная точка в области . Возьмем произвольную точку и рассмотрим какой-нибудь путь , соединяющий точку с точкой и целиком лежащий в области . Такой путь существует, поскольку область по определению является линейно связным множеством. По условию линейный интеграл в векторном поле не зависит от формы пути, значит, при фиксированном начале линейный интеграл в поле по пути будет зависеть лишь от конечной точки . Положим

.

Покажем, что скалярное поле дифференцируемо, причем его приращение в точке представимо в виде

, (3.9)

где . Согласно определению градиента, это будет означать, что справедливо равенство , т.е. векторное поле потенциально. Используя определение скалярного поля , а также свойство аддитивности линейного интеграла, получим

. (3.10)

Пусть путь, соединяющий точки и , есть отрезок . Этот отрезок может быть задан параметрическим уравнением: , . Применяя формулу (3.4) сведения линейного интеграла к определенному, получим

. (3.11)

Поскольку, по условию, векторное поле непрерывно, справедливо равенство

, (3.12)

где . С учетом равенства (3.12) правая часть формулы (3.11) принимает вид

. (3.13)

Вычисляя первое слагаемое в правой части (3.13), получим . Что же касается второго слагаемого, то, применяя к нему теорему о среднем, получим , где - угол между векторами и , а - некоторая точка из интервала (0,1), положение которой при фиксированной определяется вектором . Положим . Тогда, очевидно, . С учетом сказанного равенство (3.11) принимает вид

. (3.14)

Подставляя (3.14) в (3.10) приходим к равенству вида (3.9) откуда, как уже говорилось, следует что , т.е. что векторное поле потенциально.

Циркуляция векторного поля

Пусть, как и выше, - векторное поле, определенное и непрерывное в некоторой области пространства , а - замкнутый путь (т.е. путь, у которого начало совпадает с концом). Линейный интеграл в векторном поле по пути называется циркуляцией векторного поляпо этому пути и записывается так .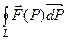

Пусть векторное поле потенциально, а - его потенциал. Тогда, как мы знаем, для любого пути справедливо равенство

, (4.1)

где - начальная, а - конечная точки пути . Если путь замкнутый, то начальная и конечная его точки совпадают, следовательно, равенство (4.1) представляется в виде . Таким образом, циркуляция потенциального векторного поля по любому замкнутому пути равна нулю.

Обратно, пусть в векторном поле для любого замкнутого пути справедливо равенство . Рассмотрим два пути и , имеющие одинаковые начала и концы. Обозначим, как и выше, через путь, противоположный пути . Тогда конец пути совпадает с началом пути , так что существует путь, являющийся объединением путей и . Положим . Очевидно, - замкнутый путь так что, согласно нашему предположению, справедливо равенство . С другой стороны, по свойствам аддитивности и антисимметричности линейного интеграла, справедливы равенства:

.

Следовательно, . Тем самым, линейный интеграл в векторном поле не зависит от формы пути так что, согласно теореме 3.1 это векторное поле потенциально.

Проведенные рассуждения показывают, что справедлива следующая

Теорема 4.1. Векторное поле потенциально тогда и только тогда, когда его циркуляция по любому замкнутому пути равна нулю.