Формула Стокса. Поток поля ротора через замкнутую поверхность

Вернемся теперь к формуле (4.24), выражающей циркуляцию векторного поля по границе ориентированной поверхности . Сравнивая ее правую часть с правой частью формулы (5.3), приходим к равенству . Таким образом, формула, выражающая циркуляцию векторного поля по границе ориентированной поверхности , принимает вид

. (6.7)

Равенство (6.7) носит название формулы Стокса и выражает тот факт, что циркуляция векторного поля по границе ориентированной поверхности равна потоку ротора этого поля через саму ориентированную поверхность.

Выше, в §4, определяя ротор векторного поля как ротор матрицы его производной в рассматриваемом базисе, было сказано, что это понятие не зависит от выбора базиса, а определяется самим векторным полем. Теперь мы имеем возможность обосновать данное утверждение. Рассмотрим в области пространства, где определено векторное поле 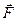, некоторую точку и пусть - единичный вектор, исходящий из этой точки. Проведем через точку плоскость, перпендикулярную вектору , и рассмотрим на ней какую-либо фигуру , содержащую внутри себя точку . Будем считать плоскую поверхность ориентированной посредством выбора в каждой точке вектора нормали равного вектору . Обозначим через границу поверхности , направление обхода по которой согласовано с выбранной ориентацией этой поверхности (см. рис 6).

Согласно формуле Стокса (6.7), имеет место равенство

.

Применяя к интегралу в правой части этого равенства теорему о среднем, получим

, (6.8)

где - некоторая точка поверхности . Деля обе части равенства (6.8) на площадь и переходя к пределу, когда поверхность стягивается в точку , приходим к формуле

. (6.9)

Очевидно, правая часть формулы (6.9) есть величина, определяемая самим векторным полем 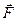, точкой , вблизи которой оно рассматривается, а также направлением вектора и никак не связана с выбором какой-либо системы координат. Эта величина называется завихренностью векторного поля 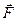в точке вокруг направления вектора . Как следует из формулы, (6.9) вектор имеет направление, вокруг которого завихренность векторного поля 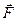в точке оказывается наибольшей, а длина вектора - есть численное значение этой наибольшей завихренности.

Пусть теперь - произвольная область в пространстве , ограниченная кусочно-гладкой поверхностью , наделенной естественной ориентацией, а - векторное поле, определенное и дифференцируемое в области . Поставим задачу вычислить поток .

Разобьем поверхность на две части и , используя для этого некоторую замкнутую линию разреза . Очевидно, линия разреза будет являться границей как для поверхности , так и для поверхности . Будем рассматривать как путь, направление обхода по которому согласовано с ориентацией поверхности . Тогда 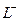- есть путь, направление обхода по которому согласовано с ориентацией поверхности .

Применяя формулу Стокса для каждой из поверхностей и , получаем

,

.

Складывая эти равенства, согласно свойству аддитивности поверхностного интеграла получаем

. (6.10)

Равенство (6.10) означает, что поток ротора любого векторного поля через замкнутую поверхность равен нулю.