Поток векторного поля через ориентированную поверхность

Рассмотрим, как и выше, векторное поле , определенное и непрерывное в некоторой области пространства и пусть - некоторая ориентированная поверхность, лежащая в области .

Представим себе область заполненной частицами жидкости (или газа), совершающими движение, при котором скорость частицы, находящейся в точке равна . Траектория движения каждой частицы представляет собой путь (называемый линией тока), касающийся векторного поля в каждой своей точке. Рассмотрим те линии тока частиц жидкости, которые пересекают поверхность . Их можно разделить на две части в зависимости от того острый или тупой угол образует направление движения по этим линиям с направлением нормали к поверхности в точке пересечения с поверхностью. Обозначим через (или ) - объем, заполняемый частицами, протекающими через поверхность за единицу времени в направлении, образующем острый (или соответственно тупой) угол с нормалью к этой поверхности. Поток векторного поля через поверхность определяется как разность объемов и , т.е. . По своему смыслу это есть баланс количеств жидкости протекающих через поверхность за единицу времени в направлениях, образующих острый и тупой угол с направлением нормали к этой поверхности. Поставим задачу вычислить поток .

Рассмотрим сначала частный случай, когда векторное поле постоянно , а ориентированная поверхность плоская. Тогда вектор нормали к поверхности , определенный в точке , один и тот же для всех точек . Объем жидкости, протекающей через поверхность за единицу времени равен объему косого цилиндра, в основании которого находится поверхность , а образующая боковой поверхности равна вектору скорости частиц жидкости, то есть вектору 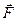(см. рис.4).

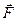Как известно, объем косого цилиндра равен объему прямого цилиндра с тем же основанием, высота которого вычисляется по формуле , где - угол между векторами и . Поэтому, если угол острый, то , , в противном случае , . Очевидно, и в том и в другом случае справедливо равенство

, (5.1)

где, как и выше, - вектор площади поверхности .

Рассмотрим теперь общий случай. Обозначим, как и выше, через вектор нормали к поверхности , определенный в точке согласно ориентации этой поверхности. Разобьем поверхность на достаточно большое число малых частей посредством разбиения и выберем на каждой из частей точку . Положим . Как мы помним, 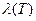называется рангом разбиения . Обозначим через поток векторного поля через поверхность 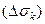. Тогда, очевидно, справедливо равенство . Для вычисления потока мы можем предполагать поверхность 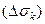сколь угодно малой по размерам. Тогда ее можно рассматривать как плоскую, полагая при этом , а вектор поля - как постоянный ( ) в пределах указанной поверхности. Используя формулу (5.1), выражающую поток постоянного векторного поля через плоскую ориентированную поверхность, можно считать, что справедливо приближенное равенство

.

Суммируя по всем частичным поверхностям, приходим к приближенному равенству

,

погрешность которого будет сколь угодно малой при достаточно малом ранге разбиения . Следовательно, для того чтобы получить точное равенство необходимо продолжить процесс дробления поверхности на все более мелкие части и перейти к пределу когда . В итоге поток векторного поля через ориентированную поверхность выразится формулой

. (5.2)

Выражение, стоящее в правой части равенства (5.2) представляет собой предел интегральной суммы и имеет специальное обозначение в виде интеграла по поверхности .

. (5.3)

С учетом обозначения (5.3) формула (5.2) принимает вид

. (5.4)

Таким образом, поток векторного поля через поверхность представляется поверхностным интегралом в векторном поле по поверхности .