
Главная Обратная связь
Дисциплины:
Архитектура (936)
Биология (6393)
География (744)
История (25)
Компьютеры (1497)
Кулинария (2184)
Культура (3938)
Литература (5778)
Математика (5918)
Медицина (9278)
Механика (2776)
Образование (13883)
Политика (26404)
Правоведение (321)
Психология (56518)
Религия (1833)
Социология (23400)
Спорт (2350)
Строительство (17942)
Технология (5741)
Транспорт (14634)
Физика (1043)
Философия (440)
Финансы (17336)
Химия (4931)
Экология (6055)
Экономика (9200)
Электроника (7621)

Дифференцируемые скалярные поля
|
|
Пусть (V) – некоторая область (т.е. открытое и связное множество) в пространстве  . Говорят, что в области (V) задано скалярное поле, если определено правило, позволяющее каждой точке
. Говорят, что в области (V) задано скалярное поле, если определено правило, позволяющее каждой точке  поставить в соответствие некоторое действительное число
поставить в соответствие некоторое действительное число  . Таким образом, скалярное поле представляет собой некоторое отображение множества (V) в
. Таким образом, скалярное поле представляет собой некоторое отображение множества (V) в  . Это отображение мы будем записывать так
. Это отображение мы будем записывать так
 ,
,  .
.
Наиболее распространенными скалярными полями, встречающимися в курсах физики, являются: значения температуры или плотности в точках некоторой материальной среды, величина давления в точках некоторой жидкостной или газовой среды, величина электрического или гравитационного потенциала в точках области пространства, где присутствует электрическое или гравитационное поле и др.
Для скалярных полей можно определить понятия предела и непрерывности. Так, число  называется пределом скалярного поля
называется пределом скалярного поля  в точке
в точке  , предельной для множества (V), если справедливо следующее утверждение
, предельной для множества (V), если справедливо следующее утверждение
 .
.
Скалярное поле  называется непрерывным в точке
называется непрерывным в точке  если
если
 .
.
Другими словами, сказанное означает, что  .
.
Пусть  ; тогда для достаточно малого по величине вектора
; тогда для достаточно малого по величине вектора  точка
точка  также будет находиться в области (V) так что существует величина
также будет находиться в области (V) так что существует величина
 ,
,
называемая приращением скалярного поля в точке  . Приращение скалярного поля представляет собой скалярную величину, зависящую от вектора сдвига
. Приращение скалярного поля представляет собой скалярную величину, зависящую от вектора сдвига  . Это значит, что скалярное поле есть функционал на множестве допустимых сдвигов
. Это значит, что скалярное поле есть функционал на множестве допустимых сдвигов  . Среди всех функционалов, определенных в
. Среди всех функционалов, определенных в  , особую роль играют линейные функционалы. При этом функционал
, особую роль играют линейные функционалы. При этом функционал  называется линейным, если
называется линейным, если
 .
.
Как известно из курса линейной алгебры, для всякого линейного функционала  существует единственный вектор
существует единственный вектор  такой, что для любого вектора
такой, что для любого вектора  справедливо равенство
справедливо равенство
 , (2.1)
, (2.1)
где, как и выше, через  обозначено скалярное произведение векторов
обозначено скалярное произведение векторов
Скалярное поле  называется дифференцируемым в точке
называется дифференцируемым в точке  , если его приращение в этой точке изменяется по закону, близкому к линейному. Это значит, что существует линейный функционал
, если его приращение в этой точке изменяется по закону, близкому к линейному. Это значит, что существует линейный функционал 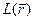 и функционал
и функционал  такие, что справедливо равенство
такие, что справедливо равенство
 ,
,
где  когда
когда  . Поскольку, как уже говорилось, всякий линейный функционал
. Поскольку, как уже говорилось, всякий линейный функционал 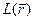 задается формулой (2.1), сказанное означает, что существует вектор
задается формулой (2.1), сказанное означает, что существует вектор  и функционал
и функционал  такие, что справедливо равенство
такие, что справедливо равенство
 ,
,  . (2.2)
. (2.2)
Вспомним определение дифференцируемости функции одной переменной, которое дается в курсе математического анализа. Согласно этому определению, функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если справедливо равенство
, если справедливо равенство
 ,
,
где  - некоторое число, а
- некоторое число, а  . Нетрудно показать, что число
. Нетрудно показать, что число  является производной функции
является производной функции  в точке
в точке  . Таким образом, дифференцируемая в точке
. Таким образом, дифференцируемая в точке  функция
функция 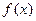 имеет там производную и при этом справедливо равенство
имеет там производную и при этом справедливо равенство
 . (2.3)
. (2.3)
Сравнивая равенства (2.2) и (2.3) можно сделать вывод, что определение дифференцируемости скалярного поля аналогично определению дифференцируемости функции одной переменной. Чтобы эта аналогия была полной достаточно определить производную скалярного поля в точке  , полагая
, полагая  . Таким образом, вектор
. Таким образом, вектор  , определяющий главную линейную часть приращения дифференцируемого в точке
, определяющий главную линейную часть приращения дифференцируемого в точке  скалярного поля
скалярного поля  , по определению есть производная скалярного поля в этой точке. С учетом сказанного равенство (2.2) может быть переписано в виде
, по определению есть производная скалярного поля в этой точке. С учетом сказанного равенство (2.2) может быть переписано в виде
 . (2.4)
. (2.4)
Вектор производной  скалярного поля в некоторой точке
скалярного поля в некоторой точке  мы будем обозначать еще так
мы будем обозначать еще так  .
.
Пусть в пространстве  задана кривая
задана кривая  , все точки которой принадлежат множеству
, все точки которой принадлежат множеству  , на котором определено скалярное поле
, на котором определено скалярное поле  . Тогда в точках кривой скалярное поле представляет собой сложную функцию переменной
. Тогда в точках кривой скалярное поле представляет собой сложную функцию переменной 
 .
.
Вычислим производную этой функции, предполагая скалярное поле дифференцируемым в точках кривой, а саму кривую – гладкой. Согласно определению, справедливо равенство
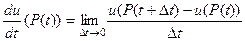 . (2.5)
. (2.5)
Введем сокращенные обозначения, полагая:  . Тогда числитель в правой части равенства (2.5) будет представлять собой приращение скалярного поля в точке
. Тогда числитель в правой части равенства (2.5) будет представлять собой приращение скалярного поля в точке  , при этом
, при этом  . Поскольку скалярное поле дифференцируемо в точке
. Поскольку скалярное поле дифференцируемо в точке  , его приращение в этой точке представляется в виде
, его приращение в этой точке представляется в виде
 .
.
Подставляя в (2.5), приходим к равенствам:


Здесь следует отметить, что второе слагаемое под знаком предела в предпоследнем равенстве исчезает, поскольку  . Полученное равенство можно записать в следующем виде
. Полученное равенство можно записать в следующем виде
 . (2.6)
. (2.6)
Очевидно, формула (2.6) представляет собой аналог известной формулы дифференцирования сложной функции с той лишь разницей, что здесь вместо числовой промежуточной переменной фигурирует точка пространства  .
.
|
Просмотров 1198 |
|
|
