Криволинейная, ортогональная система координат. Коэффициенты Ламе

ВЕКТОРНЫЙ АНАЛИЗ.

Криволинейные координаты в трехмерном геометрическом пространстве.

Криволинейная, ортогональная система координат. Коэффициенты Ламе.

Обозначим через трехмерное геометрическое пространство. Как известно, любые две точки определяют прямую линию, а участок прямой , заключенный между этими точками, называется отрезком. При этом считается, что точка есть начало, а точка - конец этого отрезка, так что отрезок направленный. Обозначим через длину отрезка . Величина , рассматриваемая как расстояние между точками , является метрикой в . Поэтому - это метрическое пространство.

На множестве направленных отрезков в пространстве определим отношение эквивалентности, считая два таких отрезка эквивалентными, если один из них может быть получен путем параллельного переноса другого. Класс эквивалентных направленных отрезков называется вектором. Множество векторов в пространстве обозначается . Вектор, представителем которого является отрезок , обозначается , а его длина равна длине отрезка и обозначается или . Каждый вектор определяется своей длиной и направлением, а его точка приложения может быть любой. Длину вектора мы будем обозначать просто , так что . Если - точка приложения вектора , а отрезок является его представителем, то говорят, что точка получена сдвигом точки на вектор . Операция сдвига точки на вектор записывается так , при этом равенство равносильно равенству .

На множестве векторов определены операции умножения вектора на число, сложения и скалярного произведения двух векторов. При умножении вектора на положительное число его направление не меняется, а длина умножается на это число. При умножении вектора на отрицательное число его направление меняется на противоположное, а длина умножается на модуль этого числа. Сложение векторов определяется как сложение представляющих их направленных отрезков, имеющих одинаковое начало, по правилу параллелограмма. Скалярное произведение двух векторов и , записываемое как или как , вычисляется по формуле , где – угол между этими векторами. Из определения скалярного произведения вытекает, что для любого числа справедливо равенство

Действительно, пусть – угол между векторами и . Если , то также будет углом как между векторами и , так и между векторами и . Поэтому

.

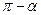Если же , то угол между векторами и , а также векторами и будет уже равен . Поэтому

.

Доказанное свойство скалярного произведения называется его однородностью по каждому из множителей. Пусть – единичный вектор (то есть вектор, длина которого равна единице). Для произвольного вектора , направленного под некоторым углом к вектору , скалярное произведение есть величина проекции вектора на направление, указанное вектором . Поскольку проекция суммы двух векторов и на произвольное направление равна сумме их проекций, справедливо равенство

.

Если – произвольный вектор, то его можно представить в виде , где – единичный вектор. Тогда, используя свойство однородности скалярного произведения и доказанное выше равенство, получаем

.

Доказанное равенство означает, что скалярное произведение является аддитивной операцией по каждому из множителей. Свойство скалярного произведения быть однородной и аддитивной операцией означает, что скалярное произведение есть линейная операция по каждому из множителей.

С операциями умножения вектора на число, сложения и скалярного произведения двух векторов множество превращается в трехмерное евклидово пространство. Очевидно, два вектора из ортогональны тогда и только тогда, когда их скалярное произведение равно нулю. Любые три единичных ортогональных друг другу вектора , , 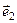образуют в пространстве ортонормированный базис. Это значит, что любой вектор представляется в виде линейной комбинации векторов , , 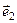, то есть справедливо равенство . Причем числа , , , называемые координатами вектора в этом базисе, вычисляются по формуле 1,2,3.

Над векторами можно определить еще одну операцию, называемую вектор-ным произведением, результатом которой является вектор, обозначаемый или .

Для определения вектора будем считать, что векторы и имеют общую точку приложения, и обозначим через тот угол между ними, величина которого не больше числа . Тогда направление вектора может быть получено поворотом направления вектора на угол вокруг оси, ортогональной этим векторам, проходящей через их точку приложения. Определим направление на оси вращения так, чтобы оно было согласовано с направлением вращения вектора по правилу правого винта. Определенное таким образом направление совпадает с направлением вектора , а его длина равна .

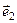Для заданных векторов рассмотрим в пространстве какой-нибудь базис , , , для которого направление векторов и совпадают. Пусть, далее, , , – координаты вектора в рассматриваемом базисе. Положим , тогда справедливо равенство . Обозначим далее через и – единичные направляющие векторы векторов и . Тогда . Очевидно, векторы и ортогональны, причем вектор может быть получен поворотом вектора вокруг оси аппликат, на которой лежит вектор , по часовой стрелке на угол 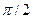. Это значит, что . Из всего сказанного следует, что справедливо равенство

.

Из полученного равенства легко следует, что операция векторного произведения линейна по первому множителю. Кроме того, она, очевидно, антисимметрична, т.е. 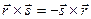и следовательно линейна и по второму множителю.

Кривой в пространстве называется всякое непрерывное отображение некоторого отрезка в . Такое отображение мы будем записывать в виде:

. (1.1)

Непрерывность отображения (1.1) означает, что справедливо следующее утверждение:

.

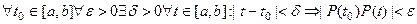Под кривой также понимают образ отображения (1.1) в пространстве .

Пусть - некоторое значение параметра. Производной от точки на кривой по параметру для значения параметра равного называется предел

.

Если такой предел существует, то кривая (1.1) называется дифференцируемой в точке (или что то же в точке ). Вектор , в этом случае всегда направлен по касательной к кривой (как к образу отображения (1.1)) в точке приложения . Кривая (1.1), дифференцируемая в каждой точке интервала , называется гладкой. Если отображение (1.1) рассматривать как уравнение движения материальной точки, где параметр играет роль времени, то вектор будет представлять собой скорость перемещения материальной точки в момент времени .

Говорят, что в пространстве заданы криволинейные координаты, если определено биективное, непрерывное в обе стороны отображение некоторого подмножества трехмерного арифметического пространства в . Для обозначения такого отображения мы будем использовать запись

(1.2)

Пусть - некоторая точка в пространстве . Рассмотрим три кривые, заданные следующими уравнениями:

, ,

, , (1.3)

, ,

где - некоторые положительные числа. Кривые (1.3), носят название координатных линий, причем, первая из них называется -линией, вторая - -линией, а третья - -линией. Очевидно, все эти линии проходят через точку . Мы скажем, что криволинейные координаты, заданные отображением (1.2), дифференцируемы в точке , если координатные линии (1.3) дифференцируемы в этой точке.

Пусть рассматриваемые криволинейные координаты дифференцируемы во всех точках пространства . Тогда для произвольной точки каждый из векторов , , будет касательным к соответствующей координатной линии в точке . Обозначим через , , единичные направляющие векторы для векторов , и соответственно. Векторы , , , зависящие от переменных , называются координатными векторами, рассматриваемых криволинейных координат. Если координатные векторы ортогональны, то говорят, что криволинейные координаты порождают в заданной точке ортогональную систему координат. Мы будем рассматривать только такие криволинейные координаты, которые в каждой точке пространства порождают ортогональную систему координат. Такие криволинейные координаты мы будем называть ортогональными.

Пусть уравнение (1.2) определяет в пространстве криволинейные, ортогональные координаты. Для произвольной точки положим , аналогично определим и . Величины , зависящие от переменных , называются коэффициентами Ламе рассматриваемых криволинейных, ортогональных координат. Согласно определению коэффициентов Ламе, справедливы равенства:

, , . (1.4)

Предполагая существование и непрерывность производных второго порядка от точки по координатам , продифференцируем первое из равенств (1.4) по координате , а второе – по координате . Тогда получим

, .

По теореме о смешанных производных левые части этих равенств равны между собой. Тогда, приравнивая их правые части, приходим к формуле

.

Используя круговую перестановку переменных , аналогично получаем:

, .

Пусть каждый из индексов , обозначает какую-либо из координат . Тогда полученные равенства можно записать в виде

. (1.5)

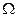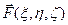Пусть - вектор-функция, определенная и дифференцируемая по каждому из аргументов на множестве и принимающая значения в пространстве . Тогда для каждой точки вектор может быть разложен по векторам ортонормированного базиса , ,

. (1.6)

Считая, как и выше, одной из координат и дифференцируя по ней равенство (1.6), получаем

. (1.7)

Формула (1.7) показывает, что для того, чтобы разложить вектор по базису , , достаточно знать разложение по этому базису векторов , т.е. знать скалярные произведения

. (1.8)

Для вычисления скалярных произведений (1.8), прежде всего, заметим, что если , то и потому

.

Следовательно, справедливо равенство

. (1.9)

В частности

. (1.10)

Далее, считая точку приложения вектора фиксированной, заметим, что траектория движения его конца при изменении координаты представляет некоторую кривую на сфере единичного радиуса, центр которой находится в точке приложения вектора . Вектор , будучи касательным к этой траектории, очевидно, ортогонален радиус-вектору точки на сфере, проведенному в точку касания, т.е. вектору . Поэтому справедливо равенство

, . (1.11)

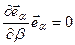Для вычисления произведения вида когда , умножим обе части равенства (1.5) скалярно на вектор . Тогда, учитывая что: , , , получаем

. (1.12)

Полагая в (1.12) 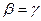, согласно (1.10), приходим к равенству

. (1.13)

Наконец, умножим равенство (1.5) на вектор , считая, что . Тогда получаем

. (1.14)

С учетом (1.9) равенство (1.14) может быть еще переписано так

. (1.15)

Пусть теперь - какая-либо перестановка переменных . Тогда, как следует из (1.11) – (1.13), справедливы разложения:

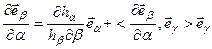, . (1.16)

Умножая разложение (1.7) скалярно на векторы , и используя формулы (1.16), приходим к равенствам:

, (1.17)

. (1.18)

Как будет показано ниже, в векторном анализе большую роль играют две операции над координатами векторов . Первая из них, называемая дивергенцией вектора 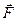, вычисляет числовую величину согласно следующей формуле

(1.19)

Вторая операция вычисляет векторную величину 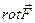, называемую ротором вектора 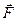, координаты которого для любой круговой перестановки переменных выражаются формулами:

. (1.20)

В развернутом виде формула (1.20) записывается так

. (1.21)

Вычисляя сумму (1.19) с использованием формул (1.17), получим

.

Вынося в правой части равенства за скобку множитель и группируя оставшиеся в скобке слагаемые, приходим к формуле

. (1.22)

Для вычисления правой части формулы (1.20) воспользуемся равенствами (1.18). Тогда получим

.

Учитывая формулу (1.15) (где и нужно поменять местами), окончательно получаем

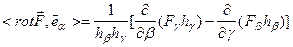. (1.23)

Пусть - некоторая функция определенная и дважды дифференцируемая в области 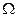. Тогда для любой точки пространства определен вектор , называемый градиентом функции и вычисляемый по формуле

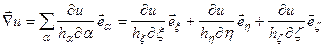. (1.24)

Положим . Тогда справедливы равенства:

, , . (1.25)

Подставляя координаты вектора 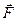в формулу (1.23), получаем

.

Следовательно, справедливо равенство

. (1.26)

Рассмотрим операцию , вычисляющую дивергенцию градиента функции трех переменных. Она играет важную роль в математической физике, имеет специальное обозначение и называется оператором Лапласа. Таким образом, согласно определению, справедливо равенство . Подставляя выражения (1.25) для координат вектора 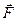в формулы (1.22), (1.23), приходим к равенствам:

, (1.27)

Формула (1.27) является выражением оператора Лапласа в криволинейных ортогональных координатах.