Криволинейные координаты, определяемые через декартову систему координат

Пусть в пространстве выделена некоторая точка , называемой началом отсчета, и заданы три единичных, ортогональных друг другу вектора , , . Тогда отображение позволяет отождествить пространство с евклидовым пространством . Обозначим через - координаты вектора в базисе , , . Тогда уравнение, определяющее положение точки в пространстве представляется в виде

. (1.28)

Очевидно, координатные и 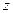-линии, проходящие через точку , представляют собой прямые, параллельные векторам , , соответственно. Дифференцируя точку по ее координатам, приходим к выводу, что все коэффициенты Ламе постоянны и равны единице, а координатные векторы в каждой точке выражаются равенствами: , , . Определенная таким образом в каждой точке пространства ортогональная система координат, координатные векторы которой одни и те же для всех точек, называется декартовой.

Пусть 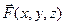- вектор-функция, определенная и дифференцируемая по каждому из аргументов в пространстве . Тогда для каждой точки 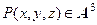разложение вектор-функции 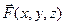по базису запишется так

.

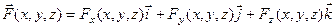Формулы (1.22), (1.23) в данном случае представляются в виде:

. (1.29)

. (1.30)

Формулы (1.29) и (1.30) являются выражением операций дивергенции и ротора вектор-функции 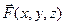в декартовых координатах.

Если - функция, определенная и дважды дифференцируемая в пространстве , то, согласно формулам (1.24), (1.26), ее градиент и оператор Лапласа в декартовых координатах представляются так:

, (1.31)

. (1.32)

Пусть в пространстве задана декартова система координат , , , . Пусть также задано биективное непрерывно дифференцируемое в обе стороны отображение некоторого множества в пространство . Всякое такое отображения определяется некоторым набором функций:

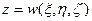, , , . (1.33)

Отображение 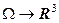, заданное набором функций (1.33), позволяет ввести в пространстве криволинейные координаты посредством отображения , представленного уравнением

. (1.34)

В дальнейшем, в целях сокращения объема, занимаемого математическими выкладками, мы будем использовать компактную форму записи частных производных вида или . Так, например, вместо мы будем писать , а вместо будем писать и т.п.

Пусть - какая-либо перестановка переменных . Равенство (1.34) можно рассматривать как уравнение -линии, если считать переменным параметром, а 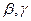- постоянными величинами. Тогда касательный вектор к -линии выражается формулой

.

С использованием компактной формы записи условие ортогональности введенных координат запишется так

, (1.35)

а коэффициенты Ламе и координатные векторы будут вычисляться по формулам:

(1.36)

. (1.37)

Определим вспомогательные векторы , полагая

.

Тогда, как легко следует из равенств (1.35), (1.36), справедливы равенства:

, (1.38)

где , если и . Векторы и позволяют определить матрицу строк и матрицу столбцов , согласно формулам:

, . (1.39)

Перемножая эти матрицы и учитывая (1.38) получим

, (1.40)

где - единичная матрица. Равенство (1.40) показывает, что матрица является обратной к матрице , т.е., что .

Вернемся теперь к равенствам (1.33). Их можно рассматривать как систему уравнений, определяющих переменные как неявные функции от переменных . Продифференцируем эти уравнения, например, по переменной считая функциями этой переменной. Тогда приходим к системе уравнений относительно производных :

. (1.41)

Аналогичные системы получаются путем дифференцирования (1.33) по переменным или 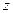. Систему (1.41) удобно записать в векторно–матричной форме. Для этого положим

.

Тогда (1.41) и подобные ей системы можно записать в виде следующих равенств:

, , . (1.42)

Умножая равенства (1.42) на матрицу и учитывая (1.40) приходим к формулам, выражающим производные неявных функций по переменным :

, , . (1.43)

Формулы (1.43) позволяют найти выражения для градиентов функций . Действительно, согласно формулам (1.31) и (1.37), справедливы равенства:

, , . (1.44)

, , . (1.45)

Равенства (1.44), (1.45) показывают, что градиенты криволинейных координат как функций декартовых координат направлены вдоль соответствующих координатных линий, а их модули обратны по величине соответствующим коэффициентам Ламе.

Предположим теперь, что криволинейные координаты заданы уравнениями вида: , , . Тогда условие их ортогональности равносильно условию ортогональности векторов: , , . При этом для каждой точки координатные векторы вычисляются по формулам:

, , .

Рассмотрим примеры криволинейных, ортогональных координат в пространстве , определяемых посредством задания некоторой декартовой системы координат .

Цилиндрические координаты. Для произвольной точки обозначим через ее проекцию на плоскость . Пусть далее параметры представляют собой полярные координаты точки на указанной плоскости. Тогда справедливы равенства:

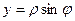, , , (1.46)

Набор чисел называется цилиндрическими координатами точки . Выражая декартовы координаты точки по формулам (1.46) и подставляя в (1.28), приходим к следующему уравнению, определяющему положение точки через ее цилиндрические координаты:

. (1.47)

Как нетрудно видеть, координатная r-линия есть луч, проходящий через точку перпендикулярно оси , начало которого находится на этой оси. Координатная j -линия есть окружность, проходящая через точку параллельно плоскости , центр которой находится на оси . Координатная же 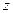-линия есть прямая, параллельная оси . Дифференцируя (1.47) по цилиндрическим координатам, вычисляя нормы и нормируя полученные векторы, приходим к равенствам:

, , ,

, , .

Непосредственной проверкой нетрудно убедиться в том, что все эти векторы ортогональны друг другу. Следовательно, цилиндрическая система координат ортогональна.

Пусть 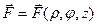- вектор-функция, заданная разложением по цилиндрической системе координат

.

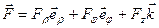Тогда, согласно (1.22), (1.23), справедливы равенства:

,

.

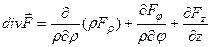Если - дважды дифференцируемая функция, то, согласно формулам (1.24), (1.26), справедливы равенства:

,

.

Сферические координаты. Для каждой точки пространства обозначим через ее расстояние до начала координат, через - угол между вектором и осью , и пусть - тот же угол, что и в цилиндрических координатах. Набор чисел называется сферическими координатами точки . Нетрудно показать, что справедливы следующие равенства:

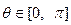, , , , , . (1.48)

Подставляя выражения декартовых координат по формулам (1.47) в (1.27), приходим к уравнению, определяющему положение точки через ее сферические координаты:

. (1.49)

Как нетрудно видеть, координатная -линия есть луч, проходящий через точку , начало которого находится в начале координат. Координатная -линия представляет собой окружность, проходящую через точку перпендикулярно плоскости , центр которой находится в начале координат. Координатная же -линия здесь та же, что и в цилиндрических координатах. Дифференцируя точку , согласно уравнению (1.49), по ее сферическим координатам и нормируя полученные векторы, приходим к равенствам:

, , ,

,

,

.

Непосредственной проверкой легко убедиться в том, что все координатные векторы ортогональны друг другу, так что сферическая система координат ортогональна.

Формулы, выражающие дивергенцию и ротор ветор-функции , заданной своим разложением по сферической системе координат, а также градиент и оператор Лапласа функции 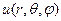запишутся так:

,

,

,

.

Упражнения. Ниже приводится ряд примеров криволинейных координат, определяемых для некоторой декартовой системы координат. Для каждой из них описать координатные линии и убедиться в их ортогональности, найти коэффициенты Ламе и координатные векторы, найти выражения для дивергенции и ротора вектор-функции, а таже для градиента и оператора Лапласа скалярной функции данных криволинейных координат.

1. Эллиптические цилиндрические координаты определяются уравнениями:

, , .

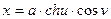2. Параболические цилиндрические координаты задаются формулами:

, , .

3. Биполярные координаты определяются формулами:

, , .

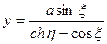4. Координаты вытянутого сфероида задаются так:

, , .

5. Координаты сплющенного сфероида определяются уравнениями:

, , .

6. Параболические координаты задаются формулами:

, , .

7. Тороидальные координаты определяются так:

, , .

8. Бисферические координаты задаются уравнениями:

, , .

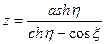Скалярные поля.